О пропускной способности модемов OFDM в радиоканалах с замираниями сигнала

В настоящее время для передачи цифровых потоков по радиоканалам с замираниями сигнала широко используются модемы сигналов с ортогональными поднесущими (Orthogonal Frequency Division Modulation – OFDM) [1; 2]. Используемый в этих модемах многоканальный способ позволяет передавать по радиоканалам с замираниями цифровую информацию со скоростью, которая недостижима в модемах, использующих одноканальный способ передачи сообщений. В настоящей статье рассматривается построение модемов OFDM и определяется пропускная способность этих модемов и параметры, от которых она зависит.

1. Принцип работы модуляторов OFDM

Модуляция OFDM подразумевает, что в частотном канале с полосой П = NF размещают N ортогональных поднесущих с частотным интервалом между ними F = 1/T, где Т – длительность одного символа на каждой поднесущей, она же является интервалом ортогональности. Ортогональность поднесущих означает, что усредненное за время Т произведение сигналов на двух разных поднесущих равно нулю, т. е. интеграл от произведения сигналов на двух разных поднесущих за время Т равен нулю. Частоты поднесущих определяются из выражения fk = fо + kF, (1) где к - номер поднесущей (к = 0,1, 2, ..., N - 1); f^ -нижняя частота сигнала, в частном случае без переноса сигнала OFDM в радиодиапазон f^ = 0, тогда fk = kF. В модуляторе OFDM входной цифровой поток данных разбивается на N потоков, в результате каждая поднесущая модулируется цифровым потоком данных с гораздо меньшей скоростью [3; 4]. Поскольку в отдельном канале скорость передачи невелика, перед каждым символом вводится защитный временной интервал, в течение которого передается фрагмент предыдущего символа. Благодаря защитному интервалу, который может достигать величины 0,25Т, удается успешно бороться с замираниями сигнала в канале. Каждая поднесущая может модулироваться двухпозиционной или четырехпозиционной фазовой модуляцией (PSK или QPSK), а также 16-, 64-, или 256-позиционной квадратурной амплитудной модуляцией (16QAM, 64QAM, 256QAM). Соответственно на каждой поднесущей один модулирующий символ за время Т будет передавать от 1 до 8 бит информации. Для реализации видов модуляции QPSK и QAM необходимы косинусносинусные генераторы (КСГ). Современные методы ЦОС позволяют существенно упростить реализацию модемов OFDM. В цифровых модемах OFDM частота дискретизации Fд выбирается такой, чтобы на интервале длительности одного символа Т укладывалось ровно N отсчетов, т. е.

F ^ = N / T = NF . (2)

С учетом этого и принимая во внимание, что exp( jx ) = cos x + j sin x , запишем в комплексном виде модулированный символом S k сигнал КСГ с частотой f_k с учетом дискретного времени при ЦОС:

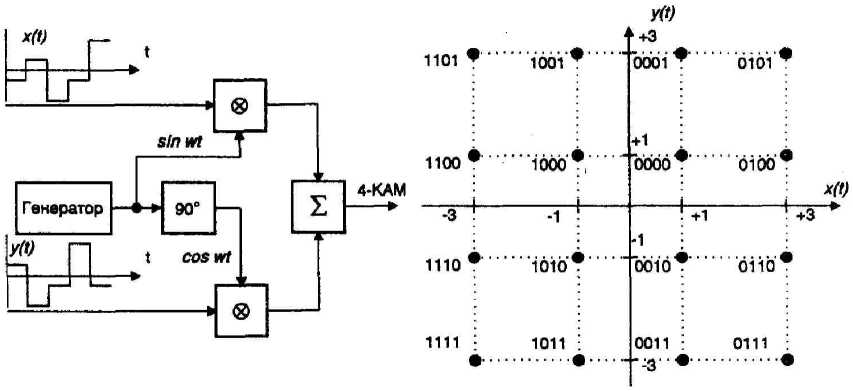
Рис. 1. Схема модулятора КСГ при 16QAM и созвездие сигналов S_k при 16QAM

Fig. 1. Schematic of the KSG modulator at 16QAM and the constellation of S_k signals at 16QAM

S k ( n ) = S k exp( j2 n kn / N ).                              (3)

На рис. 1 приведена схема одного КСГ, модулируемого квадратурной амплитудной модуляцией 16QAM, а также созвездие символов S_k при 16QAM.

Из рис. 1 видно, что четыре модулирующих бита разбиваются на две группы по 2 бита, эти два бита преобразуются в четыре уровня напряжений –3, -1,1 и 3, которые с помощью перемножителей изменяют амплитуду и фазу колебаний косинуса и синуса. Причем первые два бита воздействуют на косинус, а вторые два бита - на синус. Затем результаты перемножения суммируются. На выходе сумматора получим гармоническое колебание с частотой КСГ f k , амплитуда и начальная фаза которого однозначно определяется четырехразрядной входной кодовой комбинацией в соответствии с приведенным на рис. 1 созвездием сигналов КСГ при 16QAM [3; 4]. Если мы просуммируем сигналы всех КСГ и разделим эту сумму на число КСГ, то получим формулу обратного дискретного преобразования Фурье (ДПФ):

• 1    N — 1

s ( n ) = — У S_k exp( j2 п kn / N ),

N k = 0

где n = 0 ... N - 1.

Отсюда следует, что в модуляторах OFDM реализуется алгоритм обратного ДПФ. Так как exp jx ) = cos x + j sin x , то при вычислении ДПФ необходимо знать значения cos x и sin x . Если бы функции косинуса и синуса были монотонными, как, например, функция арктангенса, то при табличной организации вычисления cos x и sin x потребовалось бы 2 N ² ячеек памяти, так как входящие в аргументы косинуса и синуса значения k и n

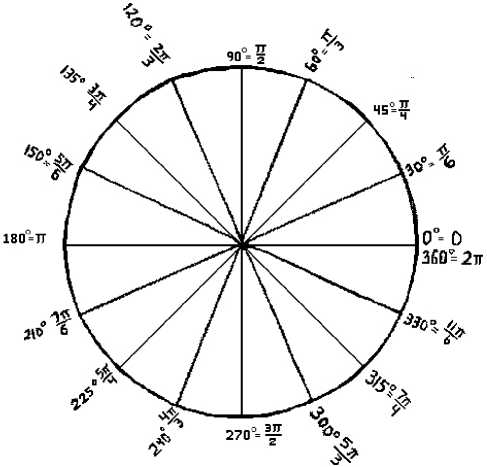
Рис. 2. Пример значений косинуса и синуса на окружности единичного радиуса при N = 16

Fig. 2. An example of the values of the cosine and sine on the circle of unit radius at N = 16

изменяются от нуля до N - 1. Но в силу периодического характера функций cos x и sin x число ячеек памяти для этих функций составит всего 2 N ячеек. На рис. 2 приведен пример значений функций cos x и sin x с шагом 22,5 градуса на окружности единичного радиуса при N = 16, причем абсциссы указанных точек на окружности соответствуют значению косинуса, а ординаты – значению синуса.

Если значения косинуса и синуса занесены в ячейки памяти, то для вычисления обратного ДПФ по приведенной выше формуле необходимо лишь определять номера ячеек памяти в зависимости от значений к и n. Так при к = 0 для любого числа n косинус равен единице, а синус равен нулю, т. е. используется только одна пара ячеек памяти. При к = 1 перебираются все ячейки памяти по часовой стрелке на окружности рис. 2 по мере увеличения числа n от нуля до N - 1. При к = 2 ячейки памяти перебираются с шагом 2 по часовой стрелке на окружности рис. 1 при этом делается два круга. При k = 3 ячейки памяти перебираются с шагом 3 по часовой стрелке на окружности рис. 1, при этом делается три круга и т. д. При к = N/2 поочередно используются только две пары ячеек памяти с номерами 0 и N/2, в которых косинус равен 1 или -1, а синус равен нулю. Из вышеизложенного вытекает следующий алгоритм определения номеров h пар ячеек памяти со значениями косинуса и синуса в зависимости от значения k:

h = 0, h = h + к при h < N, h = h + k - N при h > N.

Этот алгоритм соответствует операции сложения по модулю N . Число пар ячеек памяти, участвующих в одном цикле вычисления обратного ДПФ, равно N . При завершении по приведенной выше формуле цикла вычисления обратного ДПФ мы имеем значение s ( n ) в виде пары чисел - действительной и мнимой частей. Эти числа с помощью цифро-аналоговых преобразователей (ЦАП) преобразуются в уровни напряжений, которые участвуют в переносе сигнала модулятора OFDM в радиодиапазон по квадратурной схеме, аналогичной схеме на рис. 1. Далее этот радиосигнал излучается передатчиком в эфир.

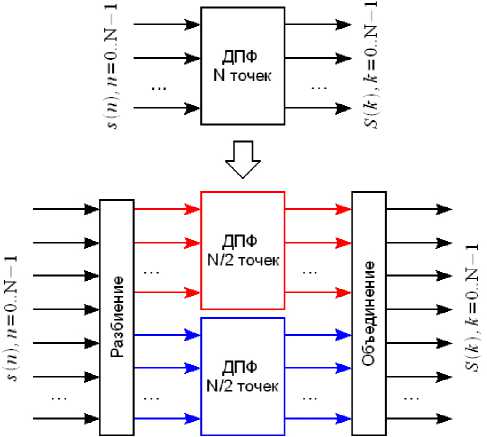
Рис. 3. Замена N -точечного ДПФ двумя N /2-точечными ДПФ

Fig. 3. Replacing an N-point DFT with two N/2-point DFTs требуют для реализации больших вычислительных затрат. От этого недостатка свободно быстрое преобразование Фурье (БПФ) [5; 6]. Идея БПФ состоит в следующем: если одно ДПФ на N точек (отсчетов) заменить вычислением двух ДПФ по N/2 точек, то это приведет к уменьшению количества операций в 2 раза. Замена N-точечного ДПФ двумя N/2-точечными ДПФ представлена на рис. 3

При этом каждое из N /2– точечных ДПФ также можно вычислить путем замены N /2-точечного ДПФ на два N /4-точечных. В этом случае количество вычислительных операций равно N ²/4. Таким образом можно продолжать разбиение исходной последовательности до тех пор, пока возможно деление последовательности на 2. В результате такого разбиения вычислительная сложность БПФ уменьшается и составляет всего ( N /2)log 2 ( N ) комплексных операций умножения и сложения вместо N ²/2 операций при ДПФ.

Будем считать, что допустимое замирание радиосигнала не должно превышать 0,25 от длительности посылки Т модема OFDM. В этих условиях для нормального приема радиосигнала с замираниями должны выполняться условия:

1 ₃ 0,25 T , T = 4 t ₃ , (4) т. е. длительность символа на каждой поднесущей должна в четыре раза превышать длительность замираний. Если задана скорость подлежащего передаче цифрового потока В , то для его передачи по радиоканалу с замираниями с помощью модема OFDM число поднесущих модема должно определяться из условия

N = BT . (5)

Это соотношение справедливо при использовании двухпозиционной модуляции поднесущих. Если использовать многопозиционные виды модуляции поднесущих, то число поднесущих уменьшается и определяется по формуле

N = BT /log₂ M , (6) где М – число позиций (вариантов) сигнала при многопозиционных видах модуляции. Так как процессоры БПФ выпускаются с числом точек N = 2 ^m , где m – целые числа, то рассчитанные по приведенным выше формулам значения числа поднесущих округляются в большую сторону до целых значений N = 2.

Приведем пример расчета параметров модема OFDM, который должен передать цифровой поток со скоростью В = 10 Мбит/сек по радиоканалу с замираниями сигнала длительностью до t _з = 0,2 мс. Тогда при указанных выше условиях нормального приема длительность символа на каждой поднесущей будет равна Т = 4 t _з = 0,8 мс.

Определим число поднесущих модема OFDM по выражению (5) при использовании двухпозиционной модуляции каждой поднесущей, например PSK:

N = BT = 10 х 10⁶ х 0,8 х 10 ^{- 3} = 8000.

Округляем это число до ближайшего большего числа N = 8192 при m = 13. В таблице приведены гипотетические параметры процессоров БПФ, на которых реализуются модемы OFDM.

Из этой таблицы выбираем процессор БПФ с числом точек N = 8192. Дополнительным требованием к процессору БПФ является то, чтобы время обработки этих точек (отсчетов сигнала) t о у процессора было меньше длительности символа Т на каждой поднесущей. Этому требованию процессор БПФ с числом точек N = 8192 не удовлетворя-

Таблица. Параметры процессоров БПФ Table. FFT processor parameters

Число точек N Время обработки tо, мс Число точек N Время обработки tо, мс 256 0,04 8192 1,5 512 0,08 16384 3,2 1024 0,15 32768 6,5 2048 0,3 65536 15,0 4096 0,7 131072 30,0 ет, т. к. у него tо = 1,5 мс, что почти вдвое превышает длительность символа Т = 4tз = 0,8 мс. Чтобы обойти эту проблему, используем в модеме OFDM четырехпозиционную модуляцию каждой поднесущей, например QPSK. Тогда число поднесущих определим по выражению (6)

N = BT / log₄ 4 = 8000 / 2 = 4000.

Как видно из результата, число точек N уменьшается в два раза. В этом случае подходит процессор с числом точек N = 4096. В этом процессоре БПФ время обработки t о = 0,7 мс, что меньше 0,8 мс. Таким образом, этот процессор подходит для построения модема OFDM, который удовлетворяет указанным выше требованиям по пропускной способности передачи цифрового потока со скоростью В = 10 Мбит/сек в радиоканале с замираниями сигнала длительностью до t _з = 0,2 мс.

• 4.    Анализ пропускной способности модемов OFDM в радиоканалах с замираниями

Приведенные выше расчеты свидетельствуют, что скорость передачи цифрового потока В или пропускная способность модемов OFDM в радиоканалах с замираниями сигнала зависит от длительности замираний сигнала t _з, числа точек N процессора БПФ, времени обработки этих точек процессором t ₀ и вида модуляции поднесущих, определяющего число позиций М сигнала на каждой поднесущей. Используя выражения (4), (5) и (6), увяжем эти параметры между собой и получим следующие соотношения:

B N log M /4 t ₃ ,                                 (7)

t о <  T .                                                           ⁽⁸⁾

Из этих соотношений следует, что скорость передачи цифрового потока В или пропускная способность модемов OFDM в радиоканалах с замираниями сигнала растет за счет увеличения числа поднесущих N (числа точек процессора БПФ), чис- ла позиций М сигнала на каждой поднесущей и уменьшения длительности замираний сигнала tз. При этом время обработки N точек процессором БПФ должно быть меньше длительности символа на каждой поднесущей.

Заключение

Проведенный выше анализ пропускной способности модемов OFDM в радиоканалах с замираниями сигнала показал, что она зависит от производительности процессоров БПФ, характеризующейся числом точек N и временем обработки этих точек tо, а также от длительности замираний радиосигнала tз. Например, переход от стандарта DVB-T цифрового телевидения к стан дарту DVB-T2 стал возможным с появлением процессоров БПФ с числом точек N = 32768, тогда как в стандарте DVB-T используются модемы OFDM на процессорах БПФ с числом точек N = 8192. За счет более мощного процессора БПФ пропускная способность модемов в стандарте DVB-T2 увеличилась в 4 раза по сравнению с модемами стандарта DVB-T [6; 7]. При этом следует отметить, что увеличение позиций М сигнала на каждой поднесущей также приводит к росту по закону log2 M пропускной способности модемов OFDM, но с ростом числа М снижается помехоустойчивость модемов, так как уменьшается расстояние между точками в созвездии сигналов на поднесущих частотах fk (рис. 1).