О радиопрозрачности плазменной оболочки гиперзвукового летательного аппарата

При движении аппаратов в верхней атмосфере со скоростями, превышающими скорость звука в три и более раз, образующаяся вокруг аппарата ударная волна начинает проявлять свойства ионизованного газа и плазмы. При этом возникают сбои радиообмена в диапазонах частот, используемых в системах спутниковой навигации, радиолокации и радиосвязи. Это делает проблематичным оперативное управление гиперзвуковым аппаратом и затрудняет установление причин аварий и отказов функционирования технических устройств. Проблема существует с первых дней пилотируемой космонавтики. Для разработки методов и аппаратуры, позволяющих обеспечить бесперебойную радиосвязь, необходимо изучить параметры затухания и фазы, которые показывают, как и с какими потерями радиоволны распространяются в исследуемой среде.

Исследуемая среда

При вхождении в атмосферу спускаемых аппаратов или при движении гиперзвуковых аппаратов, вокруг них образуется плазменная оболочка (рис. 1), влияющая на радиосвязь [1].

Рис.1. Структура плазменной оболочки объекта, движущегося в атмосфере с гиперзвуковой скоростью.

Толщина фронта ударной волны ( УВ ) имеет порядок длины свободного пробега молекул, что позволяет в расчётах фронт заменить поверхностью разрыва [2]. За фронтом газ образует по направлению Z слоистую структуру, но внутри слоёв газ относительно однородный. Т.н. адиабата Гюгоньо идёт круче, чем дозвуковая адиабата. Разогрев газа приводит к его ионизации и значительному повышению электропроводности.

Шевяков И.А.

О радиопрозрачности плазменной оболочки гиперзвукового летательного аппарата

В термодинамически равновесной среде концентрация заряженных частиц определяется формулой Саха [3]. Для газа, состоящего из атомов одного сорта, уравнение Саха можно записать в виде [4]:

3  113

n_e = ( 2 πm_e ) ⁴( kT ) ⁴ P _о ² h ²

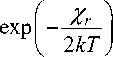
где m_e – масса электрона, χ_r – энергия ионизации и, h – постоянная Планка, T – кинетическая температура, Р о – давление нейтрального газа.

Формула (1) применима при детальном равновесии в стационарном случае, а также и для смеси газов. При полной ионизации рассматриваемой компоненты в расчёте следует переходить к следующей компоненте с наименьшим потенциалом ионизации.

В рамках феноменологического подхода радиофизические свойства исследуемой среды описываются материальными уравнениями среды. Диэлектрические свойства среды характеризуются относительной диэлектрической проницаемостью ε(ω) , а проводящие свойства – проводимостью σ(ω) . В переходной области применимы комплексные характеристики. Комплексная проницаемость ε в мнимой части содержит проводимость: ε = ε – iσ/(ε о ω) , что связано с наличием «токов потерь». Представим проводимость в комплексной форме: σ = σ_r – iσ_i , - здесь мнимая часть характеризует диэлектрические свойства среды.

Из материального уравнения и уравнения движения для электронов получаем действительную – σ_r и мнимую – σ_i компоненты комплексной проводимости:

e ² n_e ν_e

σr =             ;

m e ν_e ² + ω ²

e ² n_e   ω

σi =              .

m e ν_e ² + ω ²

Распространение волны через исследуемую среду

Газовая плазма в отличие от столкновительного ионизованного газа отличается наличием

коллективных электродинамических процессов. В частности возникают электронные плазменные колебания, но, развитию которых, препятствуют столкновения для электронов, как наиболее

подвижных частиц. Распространение радиоволн связано с этими процессами.

Итак, основными радиофизическими характеристиками исследуемой среды являются частота

столкновений электронов ν e и плазменная частота ω p (в системе СИ):

u

ν_e = ^e и ω_p λ

₂ 1/2 n e e- I ^£ o m e )

Среда становится радиопрозрачной: А) при ω p >2 π ν e имеем ω о = ω p или В) при 2 πν e > ω p будет ω_о = 2 πν_e . Здесь ω_о – критические частоты. Отражение наблюдается при частоте ω ниже критических частот, если ω p >  2 πν e , а если 2 πν e >ω p , то происходит поглощение на толщине скин-слоя δ без отражения. В качестве примеры получим значение плазменной частоты ω_p для оболочки спускаемого аппарата на высоте 75 км (скорость 5 км/с n e ≈ 10¹⁸ м^–3): ω p = 56,5·10⁹ рад/с или ν р = 9 ГГц [5]. Заметим, что переходная частотная область достаточно протяженная, в чём и заключается предмет предлагаемых исследований.

Считаем, что для длины волны λ выполняются условие: λ> ∂ , где ∂ – радиус Дебая. Распространение СВЧ поля в ионизованном газе описывается уравнениями макроскопической электродинамики [6]. Для фазового параметра – β и параметра затухания – α известны частотные зависимости:

β

2 c ² ω ²

-

ω ² _р

α ²

c ²

ω 2   2

Lk к

г

-

2     2

ν_e ² + ω ²

ν +e

ω ²

к

ω ² _р ν_e ² + ω ²

/2 f

+ 1

-

к

ω ² _р ν_e ² + ω

Lk к

ω ² _р ν_e ² + ω

,2 7

ν +e

ω ²

г

ω ² _р

/2 f

к2+«2 к e 7

-

1-

к

ω ² _р ν_e ² + ω

■² 7

к

■² 7

Краткие сообщения

Представленные уравнения позволяют построить зависимости от частоты для α и β падающего радиосигнала ω = 2 πf , например, при значении f p = 9 ГГц [7]. Графики этих зависимостей приведены на рис. 2.

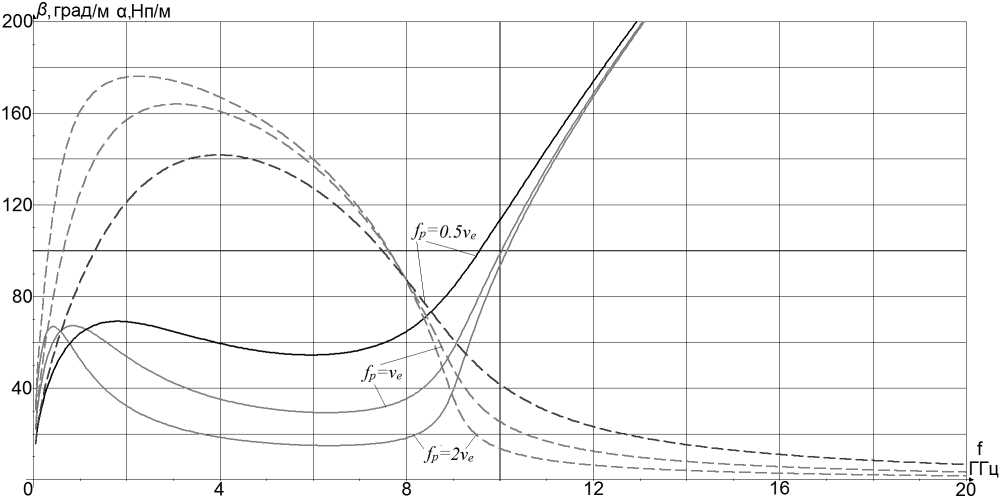
Рис. 2. Зависимости β и α (пунктир) от частоты радиосигнала

Анализируя полученные зависимости, можно отметить, что когда частота столкновений электронов незначительна, среда прозрачна для радиоволн только при значении их частоты больше плазменной, что выражается в обращении фазовой постоянной в ноль при значениях плазменной частоты меньше частоты радиосигнала. При этом значение затухания начинает резко возрастать. Это подтверждает то, что в идеальной плазме частота радиопрозрачности или критическая частота, значение которой определяет нижнюю границу для радиоволн, которые могут

распространяться в данной среде, равняется плазменной частоте.

При увеличении значения частоты столкновений электронов фазовая постоянная уже не ста-

новиться равной нулю при плазменной частоте, превышающей частоту радиосигнала, а значение постоянной затухания возрастает с меньшей скоростью, чем в чисто плазменном случае. Отсюда можно сделать вывод, что частота столкновений электронов влияет на критическую частоту для

рассматриваемой среды, которая уже не будет равняться плазменной частоте.

Для оценки изменения глубины проникновения электромагнитной волны в среду воспользу-

емся определением глубины скин-слоя δ , как обратной величины от постоянной затухания [6]:

ω δ

c

(

V

(

V

-

ω 2 _р

V 2 + № e

ν ² + ^e

ω ²

ω 2 _р

Ve2 + № e

(

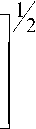
V

-

2 ω _р

2      2

V2 + №

e

\

-

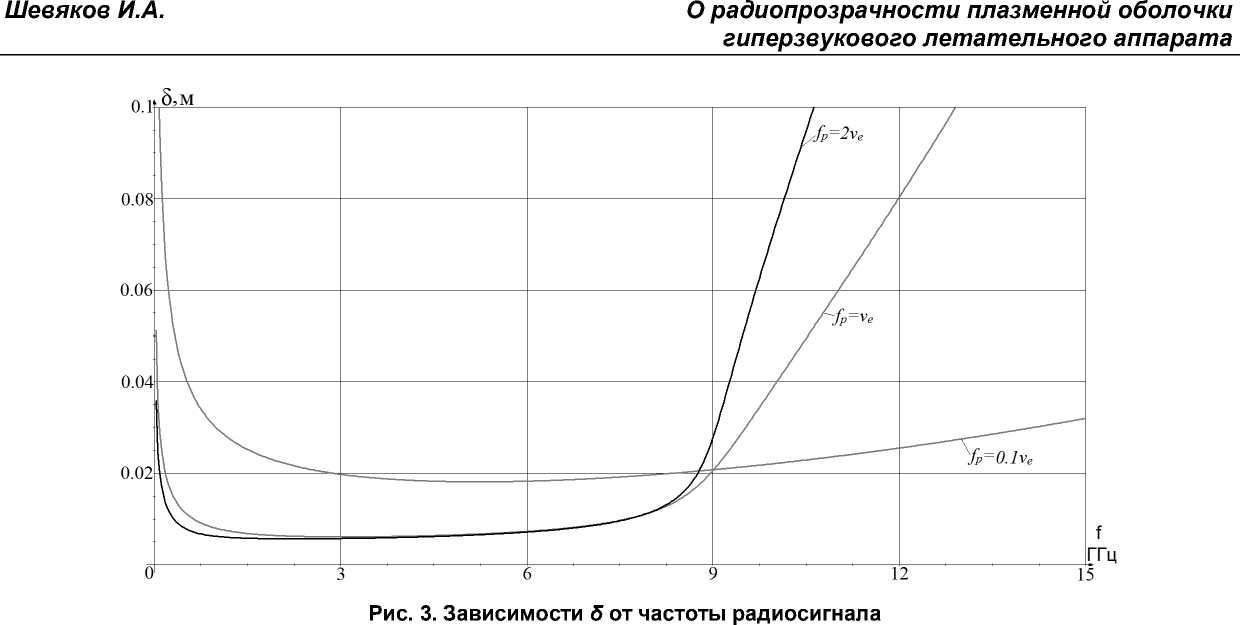
Графики, построенные по формуле (6), приведёны на рис. 3.

Несложно увидеть, что толщина скин-слоя характерно увеличивается с увеличением частоты радиосигнала в области fp = f. Однако такое резкое увеличения толщины скин-слоя характерно лишь при незначительных величинах частоты столкновений электронов (случай 1). При больших значениях νе увеличение толщины скин-слоя происходит гораздо медленнее и его значение остаётся довольно высоким во всём диапазоне частот. Это так же, как и в случае с графиками постоянных α и β, показывает, что частота столкновений электронов значительно влияет на характер распространения электромагнитной волны в столкновительной ионизированной среде. Необходимо заметить, что на низких частотах (здесь меньше 2 ГГц) зависимости на рис. 3 теряют физический смысл, т.к. длины волн превышают расчётные значения скин-слоя.

Выводы

В работе были рассмотрены свойства среды, влияющие на радиосвязь с гиперзвуковыми аппаратами. Получены зависимости для трёх важных характеристик плазменной среды - постоянных фазы и затухания, а также толщины скин-слоя. Показано, что при рассмотрении особенностей распространения электромагнитной волны в столкновительной ионизированной среде значительное влияние на радиопрозрачность оказывает частота столкновений электронов и, следовательно, частота радиопрозрачности уже не будет определяться только значением плазменной частоты.