О раскрасках двумерной сферы, разбитой на области

Данная работа мотивирована задачей Хадвигера - Нельсона - Эрдёша о хроматическом числе n-мерного евклидова пространства [1,2] . Требуется найти минимальное количество цветов, в которые можно раскрасить R2 таким образом, чтобы любые две точки пространства, находящиеся на единичном евклидовом расстоянии, были бы раскрашены в разные цвета.

В случае плоскости оценка хроматического числа имеет вид [3]:

5 < x(R2) < 7.

Для хроматического числа пространства R” были получены следующие оценки [4,5]:

x(R”) < (3 + .-. '    , щ.Э': > (1.239... + o(1)^n.

В 1981 г. П. Эрдёш поставил задачу поиска хроматического числа сферы S”^-1 радиуса г >  2 в R” [6]. Хроматическое число сферы при этом определяется как минимальное

(с) Сипелышков-Мурылев П. С., 2025

• (с) Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (пациопальпый исследовательский университет)», 2025

количество цветов, необходимое для такой раскраски сферв!, что две точки на сфере на единичном расстоянии не будут иметь один цвет. Под расстоянием между точками сферы можно понимать как расстояние в евклидовом пространстве, так и длину геодезической (дуги большого круга), но эти варианты эквивалентны с точностью до выбора масштаба. В трехмерном случае при г <  2 имеем x(S2) = 1, а при г = 2 хроматическое число равно 2, т.к. условие накладывается только на раскраску противоположных точек. Хроматическое число сферы S”^-1 при г >  2 исследовалось в ряде работ. Было доказано, что хроматическое число стремится к бесконечности при п, стремящемся к бесконечности. Одним из направлений исследований является характер этого роста. А.М. Райгородский показал [7-9], что хроматическое число сферы при г >  2 растет экспоненциально с ростом п. В работе [10] было показано, что при Уг >  2 : x(S2) > 4.

В 1999 г. К. Томассен предложил следующую формулировку задачи о хроматических числах двумерных многообразий без края: рассматриваются разбиения многообразия на области жордановыми дугами, каждая область покрашена в некоторый цвет, и расстояние между любыми двумя областями одного цвета строго больше единицы («nice coloring», [13]). В этой формулировке для раскраски плоскости и двумерных многообразий достаточно большого диаметра необходимо 7 цветов. Обозначим соответствующее хроматическое чисЛО Xnice'

П. Агостон в работе [11] показал, что в постановке К. Томассена требуется не менее 8 цветов, если радиус сферы достаточно велик:

Уг > 14.801... :    Xnice(S2) > 8.

В настоящей статье улучшена нижняя граница радиуса сферы, для которого справедлива данная оценка хроматического числа.

Теорема 1.

Уг > 6.372... : Xnice(S2) > 8.

Основной метод, применяемый в доказательстве, заключается в рассмотрении некоторого класса триангуляций сферы, для которых хроматическое число квадрата триангуляции не может быть меньше 8. В данной работе при переборе подграфов с небольшим числом вершин используются компьютерные вычисления, что позволяет улучшить оценку П. Агостона.

Также отметим, что хроматическое число квадратов планарных графов оценивается сверху в ряде работ, посвященных гипотезе Вегнера [15-17]. В препринте [18] заявлено, что хроматическое число квадрата планарного графа с максимальной степенью 6 не превосходит 20. В случае конечных планарных триангуляций, рассматриваемых в следующих разделах, хроматическое число квадрата триангуляции, по-видимому, не превосходит 9, но этот вопрос выходит за рамки настоящей статьи.

2.    Определения

Рассматривается задача о хроматическом числе сферы в постановке К. Томассена [13]. Пусть сфера разбита несамопересекающимися и попарно не пересекающимися жордановыми дугами на конечное число областей. Обозначим Н граф, образованный границами областей и точками, которые принадлежат 3 или более областям. Пусть G — двойственный граф для Н. По определению G планарен.

Расстояние на сфере S^ С R³ можно определять либо как индуцированное евклидовой метрикой в R³, либо понимать как длину геодезической. Очевидно, что первый вариант эквивалентен второму, если соответствующим образом пересчитывать радиус. В данной работе нам будет более удобно рассматривать в качестве расстояния длину дуги.

Определение 2.1. Расстоянием (метрическим расстоянием) между точками х,у G S²(г) будем называть длину дуги большого круга (геодезической).

Определение 2.2. Раскраска поверхности, разбитой на области, называется хорошей («nice» [13]), если все области одноцветны, имеют диаметр менвше 1, все пары областей одного цвета находятся на расстоянии больше 1, и все области односвязны.

Можно считать, что G — триангуляция сферы, поскольку число областей конечно, расстояния и диаметры отделены от 1, а значит, в окрестности точки, принадлежащей 4 или более областям, можно изменить разбиение и устранить такие точки, сохраняя условия хорошей раскраски.

Из формулы Эйлера следует, что, если в триангуляции сферы содержится п вершин, то число ребер будет 3п — 6, а сумма степеней этих вершин 6п — 12. Если в графе нет вершин степени более б, то не может быть более 12 вершин со степенью менее 6. Например, в таком графе может присутствовать ровно 12 вершин степени 5 или ровно б вершин степени 4.

Очевидно, что объединение двух смежных областей — это множество диаметра не более 2. Следовательно, имеем

Утверждение 1. Метрическое расстояние, соответствующее ребру G, не может быть более 2 при произвольном выборе вершин двойственного графа внутри соответствующих областей.

Далее мы также будем использовать расстояние между вершинами G в графе, которое не следует путать с метрическим расстоянием между точками на сфере.

Определение 2.3. Графовым расстоянием между двумя вершинами графа называем количество ребер в кратчайшем пути между этими вершинами.

Определение 2.4. Квадрат графа G — это граф G², имеющий такое же множество вершин, что и исходный граф G. Две вершины смежны в G² тогда и только тогда, когда графовое расстояние между ними в G не превосходит 2.

Утверждение 2. Пусть хорошая раскраска карты на сфере существует. Покрасим каждую вершину G² в цвет соответствующей об ласти. Тогда эта раскраска G² является правильной, т.е. любые две смежные вершины раскрашены по-разному.

В качестве примера рассмотрим на плоскости триангуляцию, состоящую из правильных треугольников. Рассмотрим бесконечный планарный граф, вершинами которого являются вершины триангуляции, а ребрами стороны треугольников. Все вершины такого графа имеют степень б. Известно, что квадрат такой триангуляции допускает раскраску в 7 цветов. В нашем случае вершинами рассматриваемого графа являются центры правильных шестиугольников из этой задачи (рис. 1).

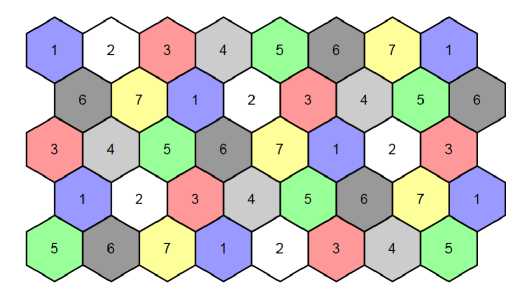
Рис. 1. Замощения плоскости правильными шестиугольниками с раскраской в 7 цветов [10]

Утверждение 3. Если G содержит вершину степени 7 или больше, то правильной раскраски G² в 7 цветов не существует, а следовательно, не существует хорошей раскраски разбиения в 7 цветов.

Действительно, такая вершина (область) и ее соседи должны иметь попарно различные цвета.

В случае подобного рассмотрения равномерной сферической триангуляции на сфере, в соответсвующем графе возникают вершины, которые имеют степень меньше 6.

Определение 2.5. Иррегулярными вершинами в G будем называть вершины, степень которых меньше 6.

Определение 2.6. Дефектом вершины графа назовем разницу между б и степенью этой вершины.

Для каждой иррегулярной вершины дефект может изменяться от 1 до 3. В соответ-свии с формулой Эйлера для графа триангуляции сферы, суммарный дефект его вершин равен 12. То есть максимальное количество иррегулярных вершин в графе может равняться 12. В силу симметрии будем рассматривать конфигурации с суммарным дефектом, не превосходящим 6.

Мы будем рассматривать локальные конфигурации подграфов планарного графа, содержащие иррегулярные вершины, и исследовать такие конфигурации с точки зрения возможности раскраски их в 7 цветов.

Определение 2.7. Назовем локальной конфигурацией подграф Н С G, который содержит группу иррегулярных вершин, образующих связный индуцированный подграф в G².

Если окажется, что некоторая локальная конфигурация графа не может быть раскрашена в 7 цветов в соответствии с заданными ограничениями, то это означает, что весь граф, содержащий ее, невозможно раскрасить. В зависимости от количества иррегулярных вершин и их суммарного дефекта в локальной конфигурации существует 13 различных типов таких подграфов с точностью до симметрии.

Определение 2.8. Соседями Z-ro порядка вершины v, I = 1, 2,... называются те вершины, которые находятся на графовом расстоянии Z от v в графе G.

Определение 2.9. к-окрестностью вершины v, к = 1, 2,... называются те вершины, которые находятся на графовом расстоянии не более к от v в графе G.

Далее всегда под графовым расстоянием (окрестностями) всегда подразумеваются расстояния (окрестности) в G, несмотря на то, что при этом речь идет о раскрасках G².

Определение 2.10. Будем считать, что иррегулярная вершина является вершиной с иррегулярной степенью к, если эта вершина имеет к иррегулярных соседей 1-го порядка.

Формируя каждую конфигурацию, мы будем выделять подграф, в котором группа иррегулярных вершин окружена множеством регулярных вершин вплоть до третьего порядка. В случае, если искомая раскраска нарушается уже на соседях меньшего порядка, мы будем оставлять на рисунке только эти вершины. Различные цвета раскраски вершин обозначены цифрами от 1 до 7. Исходя из ограничений, накладываемых на раскраску в 7 цветов, в рассматриваемых локальных конфигурациях существует запрет любым вершинам первого и второго порядка данной вершины иметь ее цвет.

Для удобства представления обозначим локальные конфигурации с изолированной иррегулярной вершиной степени 3, 4, 5 как {3}, {4}, {5}. Для локальных конфигураций, содержащих две иррегулярные вершины, аналогично этому будем использовать обозначения {3, 4}, {3, 5}, {4,4}, {5,4}, {5, 5} . Такой же характер обозначений будем использовать для всех последующих конфигураций. Здесь в индексе указывается степень соответствующей иррегулярной вершины в исходном графе. Отметим, что набор степеней не определяет подграф Н, если иррегулярных вершин больше одной.

3.    Предварительные наблюдения

Основная идея дальнейших рассуждений заключается в том, что наличие 7-раскраски (в G²) окрестности некоторого набора иррегулярных вершин всякий раз будет означать, что их суммарный дефект не меньше 6. Тогда к-окрестности ограничены циклом постоянной длины при любом к. Отсюда будет получено ограничение на радиус сферы.

Мы начинаем раскраску окрестности каждой локальной конфигурации, присваивая цвет 1 некоторой иррегулярной вершине, а ее соседям цвета 2-7. Изложим краткую схему исследования графов на возможность правильной раскраски в 7 цветов. Вначале мы будем рассматривать конфигурации, которые содержат лишь одну иррегулярную вершину.

Утверждение 4. Конфигурация {5} не допускает правильной раскраски графа в 7 цветов.

Последовательно рассматривая {4}, {5}, представленные на рис. 2, нетрудно проверить справедливость утверждения. Так, например, на рис. 2 (слева) изображена {5}. Из рисунка следует, что правильная раскраска в 7 цветов этой конфигурации нарушается, то есть невозможно раскрасить соседей второго порядка, используя 7 цветов, не нарушая существующих ограничений на запрет расстояний 1 и 2. Поясним этот вывод следующим образом. Заметим, что среди цикла вершин 2-го порядка цвета 2,..., 6 используются не более одного раза. А цвет 7 может быть использован не более трех раз. Соответственно в эти цвета можно раскрасить только 8 вершин из 10 этого цикла.

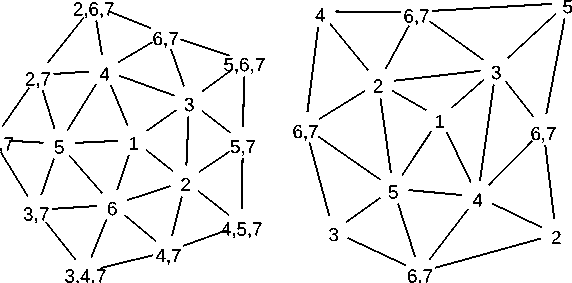
Рис. 2. Локальная конфигурация {5} (слева), {4} (справа)

Утверждение 5. Если в графе присутствует конфигурация {4}, то суммарный дефект 3-окрестности иррегулярной вершины не меньше 6.

Обозначим Lo = {го} некоторую иррегулярную верш ину (степени 3, 4 или 5). Пусть Li — это цикл, состоящий из соседей го, Lk — цикл, состоящий из вершин, которые находятся на графовом расстоянии к от го в триангуляции.

Будем считать, что некоторая вершина и находится внутри цикла Lk, разбивающего сферу (триангуляцию) на две компоненты связности, если и лежит в той же компоненте, что и Го-

Утверждение 6 ( [11]). Если внутри цикла L_n+i находятся вершины с общим дефектом q и длина L_n равна т, то L_n+1 имеет длину т + 6 — q.

Отсюда непосредственно следует

Утверждение 7. Наибольшую длину из циклов Lk имеют те, внутри которых находятся вершины с сумарным дефектом 6 (если такие существуют). Если при некотором к суммарный дефект вершин внутри Lk не менее 6, то при s > к длина L_s не больше длины Lk-

4.    Перебор триангуляций с 7-раскрашиваемым квадратом

Полный перебор расположений иррегулярных вершин с общим дефектом не более б может быть выполнен вручную, но для краткости приведем несложный алгоритм, который перебирает подграфы триангуляции, добавляя по одной вершине, пока не выполнится одно из двух условий: (1) квадрат графа не может быть раскрашен в 7 цветов, (2) суммарный дефект иррегулярных вершин, по крайней мере, 6. Следует также найти максимальную длину цикла, состоящего из вершин, которые находятся на расстоянии к от некоторой начальной. Из этой оценки далее мы получим оценку сверху на длину экватора сферы, а следовательно, оценим сверху и радиус.

Перебор подграфов триангуляций осуществляется при помощи рекурсивно вызываемой функции AddVertex(r, S,r). Параметры имеют следующий смысл: Т — построенный на текущем шаге подграф триангуляции; S — граница Т, к ребрам которой добавляются треугольники (т.е. некоторый цикл); r — дефект вершин Т, не принадлежащих S. Функция возвращает наибольшую длину цикла Lk, полностью лежащего в построенном подграфе (максимум из результатов рекурсивных вызовов и значения на текущем шаге).

Ниже приведен алгоритм работы функции AddVertex(T, S,r).

• 1)    Выберем из S первое ребро ху.

• 2)    Добавим вершину z, соединим ее с несколькими последовательными вершинами, содержащимися в ребрах S, включая х и у (от 2 до 6 вершин). Рассматриваем все варианты такого соединения. Если все варианты рассмотрены ранее, переходим к шагу 6. Иначе получим подграф Т‘ с границей S'.

• 3)    Вычислим общий дефект r‘ вер шин Т', не принадлежащих S ‘. Ес ли r‘ > 6, переходим к следующему варианту в шаге 2.

• 4)    Существует ли раскраска Т‘2 в 7 цветов? Если нет, переходим к следующему варианту в шаге 2, иначе к следующему шагу.

• 5)    Вызовем AddVertex(T‘,S',r' ).

• 6)    Возвращаем максимум из значений длин циклов, вычисленных для Т и полученных при рекурсивных вызовах.

Перебор подграфов триангуляций и вычисление максимальной длины цикла Lk осуществляется следующим образом:

• 1)    Пусть v — вершина степени d £ {3,4,5}. Li — цикл, состоящий из соседей v. Инициализируем триангуляцию Т^ графом на вершине v и ее соседях. Инициализируем очередь ребер S0^d\ добавив в нее ребра L1. Общий дефект т^ := 6 — d.

• 2)    Вычислим imax := AddVertex(T_l0^d^, S^^d^, r0^d^) для d £ {3,4, 5}.

  
  

Выведем imax := max^^x, i^x, i^x}.

Без учета симметрий графа общее число вызовов AddVertex составляет около 3 тыс., и при использовании языка программирования python с библиотекой networkx время вычислений составляет около 5 минут. Расчеты показывают, что для подграфов с 7-раскрашиваемым квадратом i_max не превосходит 10. Отсюда имеем следующую лемму.

Лемма 1 (компьютерная проверка). Любая триангуляция сферы Т, удовлятворяющая условию х(Т2) >  7. может быть разбита иа циклы, Lk- к = 0,1, 2,.... первый и последний из которых являются вырожденными, а длина остальных не превосходит 10.

Остается получить оценку на радиус сферы. Для полноты изложения приведем следующее фольклорное

Утверждение 8. Если замкнутая кривая I делит S ² (г) на две части равной площади, то длина I не меньше 2гг.

Действительно, пусть I' — образ I при центральной симметрии. Тогда I пересекает I', а значит, найдутся противоположные точки х, х' G I. Любая кривая хх' имеет длину не меньше гг.

Отсюда следует

Утверждение 9. Если замкнутая кривая I = l(t) С S ²(г), не имеющая самопересечений, непрерывно деформируется при t G [0,1] таким образом, что

• •    при t = 0 l(t) стягивается в точку, т.е. 1(0) = {хо};

• •    при t G (0,1) l(t) не проходит через хо;

• •    при t G (0,1) l(t) разбивает S 2(г) на две част и, площадь S(t) части, со держащей хо, монотонно растет с ростом t, причем S(1) > 2гг,

5.    Доказательство основного результата

то найдется такое t*, что длина l(t*) не меньше 2гг.

Достаточно рассмотреть t, при котором l(t) делит сферу на две части равной площади.

Перейдем к доказательству Теоремы 1.

Пусть хорошая раскраска в 7 цветов существует. Согласно Лемме 1, существует последовательность циклов, длина каждого из которых не превосходит 10.

Каждому ребру G, как и выше, сопоставим дугу большого круга. Таким образом, изображение G на сфере — это разбиение на сферические треугольники. Рассмотрим циклы Ci, ..., Ck в G, последовательно порождаемые окрестностью вершины хо. Согласно Лемме 1, графовая длина Ci не превосходит 10, а метрическая не превосходит 20.

Выберем такое минимальное к, что площадь области сферы с границей Ck, содержащей хо, больше 2г. Определим l(t) из Утверждения 9 при t G (0, (к — 1)/к) как произвольное стягивание Ck-i в точку хо, при котором площадь уменьшается монотонно. При t G ((к — 1)/к, 1) выберем точку Wij(t) на каждом ребре UiVj, соединяющем вершины Ck-i ii Ck- полагая, что Wij((к — 1)/к) = Ui 11 Wij (1) = Vj. причем Wij (t) движется по дуге UiVj с постоянной скоростью. Пусть l(t) соединяет точки Wij(t) в том порядке, в котором они появляются при обходе полосы из треугольников между Ck-i и Ck-

Из Утверждения 9 получаем, что найдется t*, при кото ром длина l(t* ) не меньше 2гг. С другой стороны, длина l(t*) не превосходит суммы метрических длин Ck-i и Ck, и эта сумма, не больше 2(10 + 10) = 40.

Следовательно, в случае расстояния, измеряемого как длина дуги, имеем г < — = 6.366... г

Дуге единичной метрической длины соответствует центральный угол ai = 2о. Две точки будут находиться на единичном евклидовом расстоянии в R³ и угловом расстоянии ai, если

2г

. ai n 2 .

Следовательно, в случае евклидова расстояния при наличии хорошей раскраски в 7

цветов имеем

г <

2sin 4о

= 6.372...

6.    Заключение

В данной статье были рассмотрены раскраски двумерной сферы радиуса г с запрещенным единичным расстоянием и условием К. Томассена. Показано, что сфера, радиус которой больше го = 6.372, не может быть раскрашена в 7 цветов.

Отметим, что ряд вопросов остаются открытыми. Например, кажется естественным, что при достаточно большом радиусе 8 цветов достаточно для раскраски сферы в данной постановке, но это не доказано строго. Если рассматривать раскраски сферы с запрещенным интервалом расстояний (1 — е, 1 + е) (задача Дж. Экзо, сформулированная для плоскости), то, по-видимому, также потребуется 8 цветов. Эта задача еще более сложна.

Выражаю благодарность В. А. Воронову за постановку задачи и полезные обсуждения.