О распределении чисел пар и троек одинаковых знаков на цикле двоичной мультициклической последовательности
Автор: Меженная Наталья Михайловна
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Теория вероятностей и математическая статистика
Статья в выпуске: 3, 2017 года.
Бесплатный доступ
В работе рассмотрено предельное распределение чисел пар и троек одинаковых знаков на цикле двоичной мультициклической случайной последовательности с r регистрами, заполненными независимыми в совокупности двоичными случайными величинами с равномерными распределениями, в двух случаях: 1) когда число регистров r остается фиксированным, а их длины стремятся к бесконечности; 2) когда r также стремится к бесконечности. В первом случае с помощью неравенства Берри-Эссеена получены равномерные оценки скорости сходимости.
Мультициклическая последовательность, нормальная предельная теорема, число пар одинаковых знаков, число троек одинаковых знаков, неравенство берри-эссеена
Короткий адрес: https://sciup.org/14835233
IDR: 14835233 | УДК: 519.214.5 | DOI: 10.18101/2304-5728-2017-3-78-88
Текст научной статьи О распределении чисел пар и троек одинаковых знаков на цикле двоичной мультициклической последовательности
Пусть Xj = (X0j),...,X(j-1) — независимые между собой наборы по nj случайных величин, j = 1,., r. Мультициклический генератор (см. [1])
вырабатывает псевдослучайную последовательность по правилу
r
( j )
t /а ^ t mod n
j
mod 2,
t = 0,1, K .
Величину T = n1... n r принято называть длиной цикла (1).
Мультициклический генератор позволяет получить псевдослучайную последовательность с гарантированно длинным периодом T при наличии достаточно большого числа регистров с нетождественными заполнениями. С появлением программных средств генерации псевдослучайных чисел интерес к нему существенно снизился. Но недавно выяснилось, что удается эффективно использовать современные методы теории вероятностей для исследования статистических свойств на всем цикле выходной последовательности мультициклического генератора. Это свойство выгодно отличает его от большинства других генераторов и обусловлено его специфической структурой. Свойства двоичной мультициклической слу- чайной последовательности изучались в работах [2], [3], [4]. В [2] получено распределение числа единиц ^r на цикле мультициклической последовательности вида (1) при независимых в совокупности и равномерно распределенных знаках в регистрах. Получены условия сходимости распределения ^r к распределению произведения независимых стандартных нормальных случайных величин, когда число регистров r фиксировано, а их длины п1,к,nr ^да. Также получены условия сходимости распределения ^r к логнормальному закону, когда r ^да и n1,K, nr ^да. В обоих случаях найдены оценки скорости сходимости. В работах [3] и [4] проведено исследование устойчивости предельных распределений, полученных в [2], при нарушении предположений о распределении знаков в регистрах генератора: в [3] рассмотрено распределение знаков, отличное от равномерного, а в [4] — зависимые заполнения внутри регистров.
Пусть
-
п . = £ I { Z ,= Z , 2 = к = Z. } (2)
O S i < i 2 < i k S T - 1
число наборов по k > 2 одинаковых знаков на цикле мультициклической последовательности вида (1).
Задача о распределении п k связана с задачей повторениях знаков или цепочек в последовательности независимых испытаний (см. [5], [6], [7]). В частности, в [5] получена пуассоновская аппроксимация числа пар совпавших цепочек в последовательности независимых случайных величин с полиномиальным распределением, а в [6] — обобщение этих результатов для кратных совпадений цепочек. В [7] изучено также число серий кратных повторений и момента первого появления кратного повторения цепочек. Свойства аналогичных статистик в цепи Маркова изучены в работах [8], [9], [10].
Предельное распределение числа пар и троек одинаковых знаков
Свойства распределений случайных величин п k могут быть получены из описанных выше результатов работы [2]. Если обозначить через ^ r — число единиц в Z 0, к , Z T _ 1 , то из (2)
пk = £ I 0SЦ< i 2 < ikST-1 + у I{Z = Z = = Z = 0} = C + Ck , . (3) .1 i2 .k ^r T_^r OSi<i2 <ik ST-1 Сформулируем следующие условия: А) число регистров r > 2, длины регистров п1,к, nr нечетны и взаимно просты; Б) Xj = (X0j),к,ХП-1), j = 1,...,r, — независимые между собой случай-j ные векторы длин nj, образованные независимыми (в совокупности) дво- ичными случайными величинами с равномерным распределением, т. е. P{XV = 1} = 1 -P{XV = 0} = 1, k = 0,K,n-1, j = 1,K,Г. Заметим, что при выполнении условия Б распределения случайных величин L и T -L, а значит и Ck и Ck F , совпадают. Двумерный закон Г Г S Г T S Г распределения CТ и CT_^ сосредоточен на {(x, y): x = Cn, y = CT - n, n = 0,1,..., T -1}. Утверждение 1. Пусть выполнены условия А и Б. Тогда ЕПк = 2-к+1 CT, к = 2,3, (^ ЕП4 = unTП (3nj- 2) + (8T - 6T2 + T3 - 4) , 192I j=1 1 ( ^ 3r Г Dn= — T П(3n, - 2) -T < 3 2 16 (=1 j J 16 1 1 ( ) 3r T4 Do = ^(T - 2)2Dp2 = -T(T - 2)2 П(3nj - 2) - T < -64- линии Замечание 1. Формулу для дисперсии п4 не приводим ввиду ее гро моздкости, однако ее несложно получить через центральные моменты би - номиального закона. Замечание 2. Из формул (4) и (5) видно, что свойства случайных величин п2,П3 принципиально отличаются от свойств случайных величин П4,П5,к Например, средние значения п2,П3 зависят только от длины цикла T, а Еп4 уже зависит от длин отдельных регистров. Обозначим через d(F, G) — расстояние в равномерной метрике между функциями распределения F и G на действительной прямой R: d (F, G) = sup| F (x) - G (x )|. xeR Определим случайные величины т%2= T-1(4р2- T2+ 2T) и 2п3 'П3=----3— 3 T (T - 2) T - 4 Л!”, а также введем обозначения ФГ для функции рас- пределения произведения Г независимых стандартных нормальных случайных величин, ТГ для функции распределения произведения r независимых случайных величин, распределенных по закону х2(1). Для краткости будем писать Ф1 = Ф, Т1 =Т. Замечание 3. Случайные величины у2 и iq3 равны между собой. Это будет видно из доказательства утверждения 2. Утверждение 2. Пусть выполнены условия А и Б. Тогда при к = 2,3 r d(Fк, Тr) < 2Cbe £п"ш. (8) i=1 Здесь CBE< 0,48 — константа из неравенства Берри — Эссеена для распределения суммы независимых одинаково распределенных случайных величин (см. [11]). Замечание 4. Из формулы (8) следует, что если число r > 2 фиксировано, а n1,K,nr >^, то Fnt (x) >Тr (x) при всех x е R. Замечание 5. Плотность для функции распределения Тr (x) получена в работе [12] (формула (33)) и имеет вид vr (z) = ( 2 77)-rGOr ^ 2-rz\- 2 ), где Gacd — G-функция Мейера (см., например, [13], раздел 5.3, с. 203). Замечание 6. Утверждение 2 можно переформулировать следующим образом: формула (8) эквивалентна тому, что при к = 2,3 r d(Fпк, Fr) < 2Cbe £n7m, (9) i=1 где Fr — это функция распределения суммы r независимых случайных величин, имеющих плотность распределения f (x) = J ex/2e~ex/2, x е R. V 2п Действительно, пусть с имеет распределение х2(1). Тогда плотность распределения lnс равна f 1 x) = y‘ e " y/2 = ex/2 e"ex/2. Inс x J 2ny , V2n ' y=ex Отсюда получаем (9). Замечание 7. Функция распределения Fr может быть представлена как функция распределения суммы вида 2(| v11 +k+ | vr |), в которой случай ные величины v1,k, vr независимы и одинаково распределены по стандартному нормальному закону. Такой функции распределения соответствует характеристическая функция вида 1 (2Л)772 ( - <2£)2. e2 r L 2it)) 1 + Erf —;= I 7172 JJJ где через Erf (z) обозначена стандартная функция ошибок: 2 Г у■ Erf (z) ■ —j= I e y dy. Как нетрудно убедиться, характеристическая функ-к ;0 ция одного слагаемого | v j | равна (2п) t e2 1 + Erf\ t= | I. Отсюда сра-) V V X'2 7/ зу получаем характеристическую функцию (10). Теперь перейдем к случаю, когда число регистров r также стремится к бесконечности. Здесь мы применим тот же подход, что и при доказательстве теоремы 4 работы [2]. Введем обозначения I a ■ 2 1 z lnxe-x/2dx = --(y + ln2) ^ 0.635. Q ■л I 2 It2 (lnx - a)2e-x/2dx ■ — «1,234 8 (y~ 0.577 — константа Эйлера). Параметры a ист2— это математическое ожидание и дисперсия логарифма модуля стандартной нормальной случайной величины. Рассмотрим центрированную и нормированную случайную величину »■ •ni-zEln^, к ■ 2,3. 2су r Утверждение 3. Пусть r,n1v..,nr ^да, выполнены условия А и Б. Тогда при всех x е R F (x) ^Ф(x). (11) Замечание 8. Если r, n1,K, nr ^да, выполнены условия А и Б и 1 ln n, V rj nj > 0, то E ln n2 ■ ar + o(r1/2). Значит, распределение случайной n _ ___________ „ с lni%2 - 2ra величины 3 совпадает с распределением 3 ■---2—— и (11) можно 2ctV r переписать в виде F3 (x) ^Ф(x). Замечание 9. В силу связи нормального и логарифмически нормального законов, (11) эквивалентна тому, что при к ■ 2,3 и всех у > 0 y Р{Пk< eElnnky2QTr} ^ Ju-1 e-ln2u/2du 2n 0 (в правой части стоит функция распределения логарифмически нормального закона с параметрами 0 и 1). Доказательства утверждений Доказательство утверждения 1. В работе [2] (формулы (4) и (5)) показано, что t т тА4 E5r = -, D5r = -, E[5r - - I r =l6T n (3 nj- 2). Для вычисления математических ожиданий nk, формулу (3): П2 = 2 (5 r (5 r -1) + (T-5 r)(T-5r - 1)) = ^ j=1 k = 2,3,4, преобразуем r t A2t2t +, 2 J 4 2 П = 6(5r (5r -1)(5r - 2) + (T -5r)(T -5r - 1)(T -5r - 2)) = = 2--2) k T Y T1 --+-- r 2) 12 T 3 , n = 24 (5 r (5 r -1)(5 r - Ж r - 3) + (T -5 r)(T -5 r -1)( T -5 r - 2)( T -5 r - 3)) = = -1 t--A + -1 t--A (22 - 18T + 3TЦ + -(- - 2)(- - 4)(- - 6). (15) 12 ( 2) 24 ( 2 )v 7 192 Следовательно, из (12) - (15) получаем, что т2 E^ = D5 r + 4 — T T T2 T T (T -1) "2 = 7+Т -7 = 4 . 1 ( т2 тА 1 (т т1 тА T (T - 1)(T - 2) 24 , ЕПз= -(- - 2) D5r+---= -(T - 2) - + 3 2 ( 12 3 J 2 (4 123 En4= — Е [5r- -1 + — D5 (22 - 18T + 3T2) +1^--^)(-—^)(-—6) = 4 12 ( r 2 J 24 rv ’192 = — -fr (3n. - 2) +—T (22 - 18T + 3T2) + -(T 2)(T 4)(T 6) = 192 4 =1 j 96 v 7192 r = Л-TП(3n-2) + T^(8T-6T2 + T-4). 192 j=1 Таким образом, формулы (4) и (5) доказаны. Аналогично, можно вычислить дисперсии n2 и n3 (см. (6) и (7)) и Dn2 = E l5r V t A2 t2t t2 — + 2 I 4 2 — T12 I = E 15 r — -12 2 I — - A2 = EI ^г I D,+ — = ( r 2 J 2 r 16 r =16 T И" nj — I т2 1 I " 2)+ — = — T П(3n, — 2) — T< 8 16 16 1=Г j ' T ■ 2 . 2 3 rT2 16 , Dn3= E 2 T-2) I T "J T (T —1)( T — 2) If = _(T — 2)2E I, T 7 T2 ’ r 2 J +12 — T T (T — 1) 3 12 \2 1 . If = ^(T — 2)2E I , r — T i2 2 J — T \2 i = ^(T — 2)2Dn2. Утверждение 1 доказано. Доказательство утверждения 2. В теореме 2 работы [2] было показано, что при выполнении условий А и Б расстояние в равномерной метрике между функцией распределения F- случайной величины ^ r ^r = t 1/2 (2,r — t) и функцией распределения Фr оценивается сверху вы- ражением r d(F , Фr) < Cbe£ n"m. (16) 4 r i=1 Из формулы (16) следует, что если число r > 2 фиксировано, а n1,K, nr >т, то F- (x) >Фr (x) при всех x e R. ^ r Далее воспользуемся этим результатом и формулами (13) и (14), из ко- торых следует, что П = 4 / rT+T7— T 7, П3 = 4T—21 [^ rT + п — 71 Значит, случайные величины iq2и П3 равны между собой и имеют такой же закон распределения, как и j|2. Так как при x > 0 F 2( x) = F (Vx) — F (—Tx) = 2 F (Vx) — 1, 4 r 4 r 4 r 4 r V r (x) = Ф r (Vx) — Ф r (—Vx) = 2Ф r (Vx) — 1 (в силу симметричности распределений случайной величины j|r и стандартного нормального), то d(F.2, Vr) < SUPIF-.2 (x) — Vr (x)| = sup|2F, (Vx) — 2Фr (Vx)| < r x>0 I rr I x>0 I rr I r < 2d(F^,Фr) < 2Cbe £n-1/2. r i=1 Так как распределения пар случайных величин 62 и П2, 62 и П3 совпа дают, то из последней оценки получаем (8). Утверждение 2 доказано. Доказательство утверждения 3. Заметим, что s=ini* «erf «erf «erf rfeerf - Eln П k 2ln|6r|-2Eln|6 rl ln|6 rl-Eln 16 rl GV r J 4D ln|l J V D ln|l rl . Обозначим S работы [2] имеем — число единиц в j -м регистре, j = 1,k, r. Из леммы 1 6 2 = (n, -2S,)2...(nr -2Sr)2 T = гт (nj-2Sj)2 ' =' nj- . Тогда «erf ln | 6r |= In Si + • •• + ln Sr, гдеSj = nj 1/2 | nj - 2Sj |, j = i,_, r. Центрируя и нормируя обе части фор- мулы (19), получаем, что «erf «erf «erf «erf ln|6r|-Eln|6 rl = V Sj - ESj / V D ln|6 rl j=i 1DS V k=1 . Так как случайная величина Sj распределена по биномиальному закону с параметрами nf и 1/ 2, то моменты случайных величин sj определяются формулами nj ElnkS, = — УС lnk j 2 nj1nj I 21 - nJ nj , k = i,2, . Если числа nj нечетны, то величины Elnksj конечны при всех k, j. Кроме того, из сходимости распределения случайной величины nj1/2(2Sj - nj) к стандартному нормальному закону при nj ^да следует, 2++г 2 что E lnksj сходится к -J lnkxe - x/2dx , который конечен. Значит, v по E lnksj равномерно ограничены по j. То же самое относится и к центральным моментам. В частности, Dsj сходится к ст2равномерно по j. Значит, D ln|6r l= rо2(1 + о(1)). К распределению суммы (20) можно применить неравенство Берри-Эссеена для суммы независимых неодинаково распределенных слагаемых, которое будет иметь вид (см. [14]) ln|| J-E ln|| J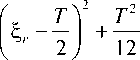
Список литературы О распределении чисел пар и троек одинаковых знаков на цикле двоичной мультициклической последовательности
- Pohl P. Description of MCV, a pseudo-random number generator//Scand. Actuar. J. -1976. -Vol. 1. -P. 1-14.
- Меженная H. М., Михайлов В. Г. О распределении числа единиц в выходной последовательности генератора Пола над полем GF(2)//Матем. вопр. криптогр. -2013. -Т. 4, № 4. -С. 95-107.
- Меженная H. М. О распределении числа единиц в двоичной мультициклической последовательности//ПДМ. -2015. -Т. 1(27). -С. 69-77.
- Mezhennaya N. М. Convergence rate estimators for the number of ones in outcome sequence of MCV generator with m-dependent registers items//Sib. Electron. Math. Reports. -2014. -Vol. 11. -P. 18-25.
- Зубков A.M., Михайлов В.Г. Предельные распределения случайных величин, связанных с длинными повторениями в последовательности независимых испытаний//Теория вероятн. и примен. -1974. -Т. 19, № 1, -С. 173-181.
- Михайлов В. Г. Предельные распределения случайных величин, связанных с многократными длинными повторениями в последовательности независимых испытаний//Теория вероятн. и примен. -1974. -Т. 19, № 1, -С. 182-187.
- Зубков А. М., Михайлов В. Г. О повторениях s-цепочек в последовательности независимых величин//Теория вероятн. и примен. -1979. -Т. 24, № 2. -С. 267-279.
- Михайлов В. Г., Шойтов А. М. О длинных повторениях цепочек в цепи Маркова//Дискрет, матем. -2014. -Т. 26, № 3. -С. 79-89.
- Михайлов В. Г. Оценки точности пуассоновской аппроксимации для распределения числа серий повторений длинных цепочек в цепи Маркова//Дискрет, матем. -2015. -Т. 27, № 4. -С. 67-78.
- Михайлов В. Г., Шойтов А. М. Многократные повторения длинных цепочек в конечной цепи Маркова//Матем. вопр. криптогр. -2015. -Т. 6, № 3. -С. 117-133.
- Тюрин И. С. Уточнения остаточного члена в теореме Ляпунова//Теория вероятн. и примен. -2011. -Т. 56. Вып. 3. -С. 808-811
- Springer М. D., Thompson W. E. The Distribution of Products of Beta, Gamma and Gaussian Random Variables//SIAM J. Appl. Math. -1970. -Vol. 18, №4, -P. 721-737.
- Бейтмен Г., Эрдейи А. Высшие трансцендентные функции, т. 1. 2-е изд. -М.: Наука, 1973. -296 с.
- Королев В. Ю., Шевцова И. Г. О верхней оценке абсолютной постоянной в неравенстве Берри-Эссеена//Теория вероятн. и ее примен. -2009. -Т. 54, № 4. -С. 671-695.


