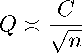О распределении числа цепочек специального вида в размеченном полном графе

Большое количество сложных систем [1] допускают интерпретацию в виде сетей или графов, где вершины являются элементами системы, а ребра отвечают за связь между ними. В таких моделях, как правило, не все вершины и связи между ними одинаковы. Для их характеризации используются специально подобранные числовые характеристики, каждая из которых приписывает то или иное свойство каждой из вершин или ребер — так называемые веса, а соответствующие графы принято называть взвешенными. Данный тип графов может быть использован в медицине для представления плотности нейронных связей [2, 3], в управлении для организации эффективного взаимодействия между командами [4], в урбанистике для демаркации регионов [5].

Графы со случайными метками на вершинах или ребрах по-прежнему остаются недостаточно изученной областью. Поиску цепочек на графах со случайными метками также посвящено небольшое количество работ. В [6] рассмотрена задача о поиске кратчайшего пути на полном графе со случайными метками, значения которых равномерно распределены на отрезке [0; 1], а в [7] получен алгоритм для поиска цепочек на подобном графе.

Однако гораздо меньшее внимание уделяется взвешенным графам, метки у которых расположены на вершинах. Такие графы широко применяются в вычислительной биологии, например, для представления аминокислот, где атомная масса каждого атома молекулы является меткой на вершине [8].

В настоящей работе рассматривается задача об аппроксимации нормальным законом распределения числа цепочек из одинаковых меток вершин на полном графе, в котором метки на вершинах независимы между собой и присваиваются вершинам в соответствии с заданным распределением на конечном множестве.

1 Центральная предельная теорема

Рассмотрим полный граф с n вершинами, n > 2. Занумеруем ребра в лексикографическом порядке в соответствии с парами номеров вершин. Каждой вершине независимо от остальных присваивается метка, которая выбирается из конечного множества {a i ,..., a m }, m > 2, с заданными вероятностями p i ,...,p m , p i + ... + p m = 1. Будем говорить, что вершины 1 <  i i < ... < i i <  n образуют цепочку меток a i ,..., a i длины l, 1 <  l < n, если a s — метка вершины i s ,s = 1,..., l. При этом поскольку граф полный, то все вершины соединены ребрами, и наше определение согласовано с классическим определением цепи на графе.

Рассмотрим случайную величину ξ , равную числу цепочек вершин [9, с. 21] на графе, состоящих из одинаковых меток as, s Е {1,..., m}, а именно

с = Е     in,... ,

1

Обозначим через N(0,1) стандартный нормальный закон распреде- ления, через

Ф(w) =

, 2

dy

— функцию распределения N(0,1), через Д — сходимость по распре- делению.

Теорема 1. Пусть l > 1, ps = Cn^a, где C > 0, (1 ) -----

<

\ m   / 2l — 1

a< 0 при некотором натуральном m > 3. Тогда

(С — EC)/VDC Д N(0,1) при n Д то,            (1)

и все моменты случайной величины (С — ЕС)/ VDC сходятся к моментам N(0,1) при n Д то.

Очевидным образом из теоремы 1 получаем следующее утвержде- ние.

2l — 1

<α≤

Следствие 1. Пусть n > l > 1, ps = Cn^a, где C > 0,

0. Тогда

(С — EC)/PD Д N(0,1) при n Д то, и все моменты случайной величины (С — ЕС)/ VDC сходятся к моментам N(0,1) при n Д то.

Теорема 2. Пусть n> l > 1, ps = Cna, где C > 0, —1 < a < 0, a  cn (i • Cp + 1)2

Q      n3(l-1/2)(a+1) , тогда для любого w ∈ R

|p ((С — EO/VD < w) — Ф(w)| < 32(1 + Ve)Q^1/2.      (2)

Замечание 1. Порядок величины Q при ps = const и n Д то: Q C

√n .

Здесь и далее запись an х bn означает, что a

0 < lim — = c < то. n→∞ b_n

Замечание 2. Порядок величины Q при ps = Cn^a, — 1 < a < 0:

О _____n³l ²_____ ₌  (3/2-3l)a-1/2

.

Q ~ n(3l-3/2)(a+1)    n

Замечание 3. Область значений параметра α, в которой правая часть оценки (2) ^ 0 :

α<

3(1 — 2l).

Сравним эту область изменения параметра α и область для него в теореме 1. При m = 3 области в теоремах 1 и 2 совпадают. При m > 3 область сходимости к нормальному закону, полученная в теореме 1, шире.

2 Доказательства теорем

Для доказательства нам понадобятся вспомогательные результаты. Так, поскольку

E1ii,...,il = ps, тогда

E^ = СП Ps

Лемма 1. Ковариация случайных индикаторов 1i1,...,il и 1j1,...,jl , если имеется k общих вершин в наборах ii,..., i' и ji,... ,ji, 1 < k < l, равна cov(1ii,...,., lji,...j) = P2l-k(1 — pk),                     (4)

тогда

X cov(1.i.1,1j1jl ) = C Ct-kps'-k (1 — Psk).

j1 ,...,jl

Если все вершины совпадают (k = l), то cov(iii,...,ii, j,...,ji) = pS (1 - pS).                         (5)

Доказательство. Рассмотрим случай, когда имеется k общих вершин, 1 < k < l. Зафиксируем их. Тогда потребуется 2l — к меток с заданными вероятностями p_s для двух цепочек меток длин l. Значит, вероятность того, что наборы вершин ii,..., i' и ji,... ,ji образуют цепочки меток, равна

E(1ii,...,ii 1_л,...,л) = pTk.

Следовательно, значение ковариации равно cov(1.i ,...,ii, 1ji„..jl) = ps-k(1 — pk).

С учетом возможных вариантов выбора k общих вершин получим

X cov(1i,ii, 1jij) = Ck E-pTk(1 - pk).

j1 ,...,jl

Пусть теперь все вершины совпадают. Тогда математическое ожидание того, что наборы вершин i1 , . . . , i и j1 , . . . , j образуют цепочки, равно

^E(1i,,...,ii 1j,,...,ji) ^—P_s-

Отсюда сразу получаем (5).

Лемма 2. Пусть p_sE (0; 1), n > 3, тогда дисперсия случайной величины ξ равна

-1

k -k 2 -k 2

^D— Cn / _v Cl Cn-l ^(ps   ^{— p}s ) ^{+ p}s^{(1 — p}s) I .         ⁽⁶⁾

k=1

Доказательство. Согласно определению случайной величины ξ

D€    52 52 ^cov(1i1,...,il, 1j1 vdl)

i1,...,il j1,...,jl

Зафиксируем k общих вершин, при этом ковариации определяются формулами (4) и (5). Выбираем k вершин Clk способами из l, а оставшиеся l — k вершин — C1-, способами. При фиксированном наборе ii,... ,in считаем число различных наборов j1 , . . . , jl, образующих цепочку одинаковых меток, при которых ровно k элементов из j1 , . . . , jl совпадают с элементами из i1 , . . . , il. Общее количество случайных индикаторов — Cnl , поэтому домножим на это выражение, тогда l-1

l          k l-k 2l-k     2l l        l

DS ^— Cn I / _vCl Cn-l ⁽p_S    ^—ps ) + p_S^{(1 —}ps) 1 .

k=1

Теперь перейдем к доказательству теоремы 1. Нам понадобится вспомогательный результат, который опирается на понятие «графа зависимостей».

Граф Г — (V, E) будем называть графом зависимостей для системы случайных величин {Xj, j E V}, если для любой непересекающейся пары множеств вершин Ai,A2 E V, таких, что нет ребер из E, соединяющих вершины в A1 с вершинами в A2, наборы случайных величин {Xi,i E Ai} и {Xi,i E A2} независимы.

Теорема 3 [Теорема 2, [10]]. Пусть {XniJN! — семейство ограниченных случайных величин для любого n: |X_ni | ≤ A_n, с графом зависимостей Г_п. Пусть Mn — максимальная степень вершины Г_п(в случае,

Nn если Гп не содержит вершин, положим Mn = 1). Пусть Sn = ^2 Xni и i=1

an, = DSn. Если существует такое целое m > 3, что

(Nn/Mn)^1/m• MnAn/^n ^ 0 при n ^ то,          (7)

тогда

(Sn — ES_n)/^_n —>N(0,1) при n ^ то.             (8)

Также все моменты (Sn — ESn)/an сходятся к моментам стандартного нормального распределения.

Построим теперь граф зависимостей для системы индикаторов {1i_1,...,i_l}. В нем будет C_n^lвершин, каждая из которых соответствует одному из случайных индикаторов. Вершины, соответствующие 1i_1,...,i_lи 1j_1,...,j_l, связаны ребром, если 1 < |{ii,... ,ii} П {ji,..., ji}| < l.

Оценим сверху максимальную степень вершины D в построенном графе зависимостей Г. Зафиксируем одну из вершин цепочки меток, соответствующих 1i_1,...,i_l. Для каждой такой зафиксированной вершины выберем l - 1 вершину из общего количества свободных вершин Cn—11 способами. Также будем учитывать петли, тогда общее выражение для верхней оценки D можно записать в виде:

D< l • C— + 1.                      (9)

Применим теорему 3 к нашему набору случайных индикаторов.

Случайные индикаторы 1i_1,...,i_lограничены сверху единицей, следовательно, можно считать, что An = 1. Число Nn — общее число вершин в графе зависимостей для системы индикаторов {1j_1,...,j_l}, значит, Nn = СП. Согласно (9)

Mn< l • Cn—i + 1.

2            1

m(2l — 1) - 2l — 1

Пусть ps ^ 0, ps = Cn^a,

< a< 0, C > 0. Вы-

полним подстановку в (6) и переобозначим в (6) k-е слагаемое через bk = Cn Ck Cn—l p2 —k (1 — pk). Тогда при n ^ то bk bk+1

n2l—k n(2l—k)a n2l—k—1n(2l—k—1)a

= n^a+1

^ bk+1 = n^—(1+a)bk,

D^ x b1 + n^—(1+a)b₁ + n^—2(1+a)b1 + ....

Значит,

D€ = bi(1 + O(n-1-a)), n ^ to, где запись f (x) = O(g(x)) означает, что f является «О» большим от g при x ^ то, то есть существует такая константа C > 0, что для всех |x| > N имеет место неравенство |f(x)| < C|g(x)|.

Тогда при n ^ то

Dl х Cnn (C1 • С^ • n(2l-1)a + nla) - n(2l—1)(a+1) _ bi, an х pn(2l-1)(a+1) х n(l-1/2)(a+1).(10)

Выполним подстановку в (7). Тогда при m > 3

/ nl У/m

\nl-1/     n(l-1/2)(a+1) ~^’ n1/mn(1/2-l)a-1/2 ^ 0,

• n1/m+(1/2-l)a-1/2 ^ 0 при ^m^) - 2^1.

Следовательно, по теореме 3 выполняется (8), что и соответствует утверждению (1) из теоремы 1.

Перейдем к доказательству теоремы 2. Воспользуемся следующим утверждением.

Теорема 4 [Следствие 2, [11]]. Пусть {XniJNn — случайные величины с графом зависимостей Г_П= (V, E). Положим, Sn = PN1 Xni и аП = DSn. Пусть Mn — максимальная степень вершины Г_п, и предположим, что |Xni| < An. Определим

Q =

NnMn^

(Т 3 σn

тогда

P /Sn  ^ESn< w\ - _ф(w)

σn

< 32(1 + Ve)Q^1/2.

Применим теорему 4 к нашей задаче. Подставим найденные ранее значения An = 1, D из (9) и an из (10) в (12). Тогда

Q<Q=

сП (i • сП- + i)² (n^(l-1/2)(a+1))³

Тем самым теорема 2 доказана.

□

Замечания 1–3 получаем из следующих соотношений. Порядок величины Q при ps = const и n ^ то:

Найдем a, — 1 < a < 0, при котором Q ^ 0:

3l—2

Q

n_________ = „ (3/2—3l)a—1/2 n(3l—3/2)(a+1)    n,

Q ^ 0 при a< 3 - 61.(13)

При m = 3 области для параметра a в (13) и (11) совпадают. Если m > 3, область, полученная в (11), шире:

1               21

1 — 21 - m(1 — 21) > 3 — 61.

3 Численные значения оценки скорости сходимости

Из приведенных в теореме 2 оценок скорости сходимости оказывается, что нужно графы достаточно большого размера, чтобы эти оценки были содержательны. Порядок полученных оценок позволяет доказать центральную предельную теорему в ряде случаев, но скорее носит для практических задач качественный, чем количественный, характер .

Естественно ожидать, что для меньшего на порядки количества вершин нормальная аппроксимация также будет работать. Изучим этот вопрос при помощи численных методов.

Пусть

Г = . E..