О размере и сложности компонент связности случайного гиперграфа
Автор: Кошелев М.М., Шабанов Д. А.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 4 (60) т.15, 2023 года.
Бесплатный доступ
В работе исследуются предельные распределения размеров и сложностей компонент связности случайного гиперграфа в биномиальной модели Н(n,k,p). Рассматривается ситуация «внутри фазового перехода», где p = p(n) представляется в виде p = l/(k-1)(n-1) при l = l(n), удовлетворяющем соотношению (l - 1)n1/3 ~ (k - 1)2/3а при фиксированном а G R. Основной результат работы состоит в получении обобщения результата Д. Олдоса (1997) о совместных предельных распределениях размеров и сложностей компонент случайного графа на случай Н(n,k,p).
Случайные гиперграфы, компоненты связности, броуновское движение, слабая сходимость
Короткий адрес: https://sciup.org/142239465
IDR: 142239465
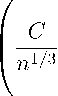
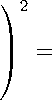
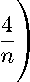
Список литературы О размере и сложности компонент связности случайного гиперграфа
- Xapapu Ф. Теория графов / пер. с англ. Москва: УРСС, 2018. 304 с.
- Erdos Р., Renyi A. On the evolution of random graphs // Publication of the Mathematical Institute of the Hungarian Academy of Sciences. 1960. V. 5. P. 17-61.
- Степанов B.E. О вероятности связности случайного графа Qm(t) f f Теория вероятн. и ее примен. 1970. Т. 15, > 1. С. 55-67.
- Luczak Т., Pitted, В., Wierman J. The structure of a random graph at the point of phase transition // Transactions of the American Mathematical Society. 1994. V. 341. P. 721-748.
- Bollobas B. Random graphs. Cambridge University Press, 2001.
- Jansen S., Luczak T., Rucinski A. Random graphs. New York: Wilev-Interscience, 2000.
- Aldous D. Brownian excursions, critical random graphs and the multiplicative coalescent // The Annals of Probability. 1997. V. 25. P. 812-854.
- Schmidt-Pruzan J., Shamir E.Component structures in the evolution of random hvpergraphs // Combinatorica. 1985. V. 5. P. 81-94.
- Behrisch M., Coja-Oghlan A., Kang M. The order of the giant component of random hvpergraphs // Random Structures and Algorithms. 2010. V. 36. P. 149-184.
- Bollobas B., Riordan O. Asymptotic normality of the size of the giant component in a random hvpergraph // Random Structures and Algorithms. 2013. V. 41. P. 441-450.
