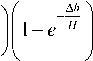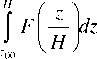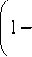О роли конвективного генератора в глобальной электрической цепи

Глобальная электрическая цепь (ГЭЦ) – распределенный токовый контур, образованный высоко-проводящими слоями верхнего слоя океана и земной коры и атмосферой, проводимость которой ничтожно мала в пограничном слое, но резко (экспоненциально) растет с высотой [Wiliams, 2009]. Согласно концепции Вильсона, сформулированной 90 лет назад, основными источниками ЭДС, поддерживающей потенциал ионосферы, служат облака, обладающие электрической структурой (прежде всего кучево-дождевые и слоисто-дождевые), а зонами возвратных токов – области хорошей погоды. Вместе с тем хорошо известно, что наряду с генераторами, находящимися в нижней части атмосферы, существенный вклад в распределение потенциала и тока ГЭЦ дают ионосферные и магнитосферные генераторы. Таким образом, состояние ГЭЦ, с одной стороны, непосредственно отражает состояние климатической системы, а с другой – испытывает непосредственное воздействие космических факторов, включая изменения солнечной активности [Мареев, 2010]. Поэтому изучение климатологии и развитие численных моделей ГЭЦ является одной из важнейших задач изучения солнечно-земных связей. И наиболее важной нерешенной проблемой теории ГЭЦ остается исследование основных генераторов, обеспечивающих поддержание ионосферного потенциала (ИП) и его вариации.

Хорошо известно, что турбулентная конвекция способствует интенсивному перемешиванию заряженных частиц в неоднородном пограничном слое, и, как следствие, генерации вертикального электрического тока [Hoppel et al., 1986; Israelsson et al., 1994; Anisimov et al., 2002; Markson, 2007]. Как правило, этот ток направлен вверх, если вблизи поверхности Земли формируется положительный объемный заряд, в частности, благодаря электродному эффекту. До сих пор, однако, нет определенности в оценке вклада конвективного генератора в ГЭЦ, что связано и с недостатком данных, и со сложностью теории [Willett, 1979; Mareeva et al., 1999; Morozov,

2006]. Дело в том, что интенсивность конвективного генератора зависит от ИП, который сам зависит от работы генератора, поэтому исследование вклада конвективного генератора в ГЭЦ требует решения самосогласованной задачи. Виллет в работе [Willett, 1979] исследовал поведение турбулентного конвективного тока в неустойчивом пограничном слое и нашел, что конвективные токи действуют как локальный генератор, способный понижать суммарную плотность направленного к земле тока на фоне заданного ИП (рис. 1). Следующим шагом должно быть изучение глобальной роли конвективного тока, т. е. определение его вклада в ИП. Этот вопрос рассматривался в работе [Morozov, 2006], где представлены оценки для ИП, но сложная параметризация генераторов ГЭЦ не позволила автору дать ясную физическую картину явления. В настоящей работе мы предлагаем простой аналитический подход к расчету ИП, индуцированного сторонними электрическими токами в атмосфере. Этот подход позволил определить потенциал, индуцированный конвективным током, и исследовать его зависимость от параметров задачи, включая суточные изменения площади конвекции на земной поверхности, дающие вклад в унитарную вариацию ИП.

Выражение для ионосферного потенциала

Прежде всего, необходимо обосновать интегральное представление ИП, индуцируемого сторонними электрическими токами в атмосфере. Объемная плотность тока J(г) включает плотность сторонних токов J (г) и ток проводимости:

^ ^      ^ ^ ^     ^^,. ^

J ( г ) = о ( г ) E ( г ) + J ™( г ) .                           (1)

Уравнение Максвелла имеет вид

^ ^    4 п ^ ^ ^ 4 п ^. ^

rot H ( г ) = —о( г ) E ( г ) + — J ( г ) .            (2)

cc

Задача состоит в том, чтобы найти возмущение электрического потенциала, порожденное распреде-

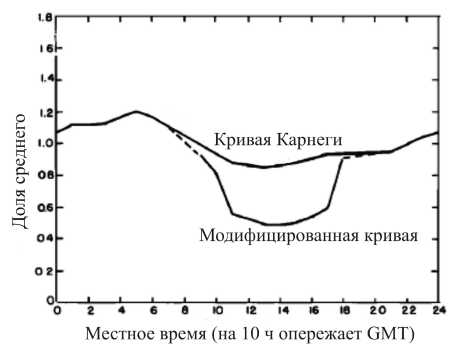
Рис . 1 . Суточная вариация полной плотности тока , на правленного к Земле ( кривая Карнеги ), с учетом влияния эффектов конвективного тока , в пункте Hay, Австралия [Willett, 1979].

ленным сторонним током, на поверхности сферы радиуса R. Мы считаем, что проводимость зависит только от радиуса и не зависит от угловых координат, т. е. σ(r), и интегрируем уравнение (2) по замкнутой сферической поверхности S:

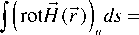
= — J J^ ( 7 )ds + —o ( r )f Ends . c_S              c _S

Легко показать, что левая часть этого уравнения равна нулю. Принимая во внимание, что электрическое поле является потенциальным, можно записать Er ( r )=–∂φ( r )/∂ r .

Будем искать на сферической поверхности радиуса R_i усредненный потенциал, порожденный сторонним током, локализованным внутри шарового слоя. Проинтегрируем уравнение (3) по r в пределах от радиуса Земли R E до Ri , приняв потенциал Земли равным нулю:

1 j dV

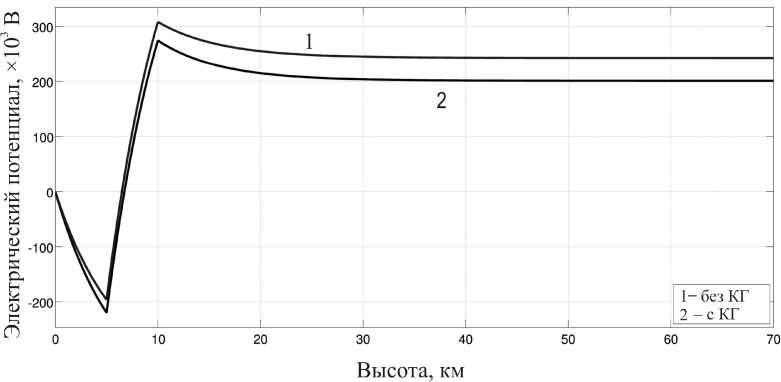
Ф=Ф ⁽ R ) = — ~~, 4 π _V σ ( r ) r ²

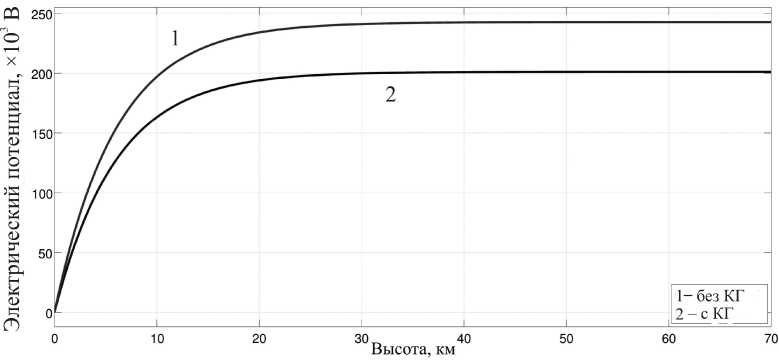
где jr (r, θ, ψ) – радиальная компонента стороннего тока Jext(r), интегрирование проводится по объему шарового слоя VС. Будем считать, что проводимость атмосферы изменяется с высотой по экспоненциальному закону: σ(r)=σ0exp((r–RE)/H), где H – характерный масштаб изменения проводи- мости, σ0 – удельная электрическая проводимость атмосферы у земной поверхности. Предположим, что слой постоянного стороннего тока jr=j0 сосредоточен внутри области h

Здесь Δh – толщина области, занятой сторонними токами, h – высота нижней границы этой области. Возмущение потенциала ионосферы равно

ϕ(Ri)=H

j₀∆ψ

4πσ₀

sin θ₀∆θexp

h-}

H )

∆h

-

1 - e ^H I. (5)

k )

В случае когда h<<R3, формулу (5) можно преобразовать, домножив ее числитель и знаменатель на R₃²

и приняв во внимание, что R₃²∆ψsinθ₀∆θ = S_⊥– это площадь поверхности объема, занятого сторонним током. Тогда возмущение потенциала определяется следующим соотношением:

ϕ(Ri)=H

j₀S_⊥4πR_E²σ₀

( h exp - k H

IH

^SE^σ

∆h

-

1 - e "

k

где σh=σ0exp(h/H) – проводимость атмосферы на нижней границе области, занятой сторонними токами, I – сила стороннего тока, SE – площадь поверхности Земли. Полученные формулы справедливы для произвольных соотношений между линейными размерами области тока и высотой h и могут использоваться для численных расчетов ИП в климатических моделях.

Выражение для конвективного тока

В соответствии со сложившимися представлениями основной вклад в ИП ГЭЦ вносят сторонние источники, обусловленные разделением электрических зарядов в облаках (в первую очередь в грозо-вых/ливневых облаках). Типичные грозовые генераторы представляют собой слои стороннего заряда с током, направленным вертикально вверх.

Сделаем некоторые оценки. Рассмотрим грозовое облако с горизонтальным масштабом порядка 10 км, Δh≈h≈H, H≈6·105 см. Характерные значения плотности стороннего тока j0≈10 нA/м2=3∙10–3CГС, проводимости атмосферы у поверхности Земли σ0≈3·10–4c–1. Тогда вклад, который дает одно грозовое облако в ИП, в соответствии с формулой (6) равен фcloud(Ru) ^ 2-10-1 СГС=60В.

Суммарный вклад в ИП всех облаков на Земле, обладающих электрической структурой «нормальной полярности», равен

^ ф^cloud (Ru) « 60B • 4 -103 = 240 кВ. i

Другим видом сторонних источников, имеющим важное значение в поддержании ИП ГЭЦ, являются конвективные генераторы. В общем случае сторонний ток представляет собой сумму токов всех облачных генераторов и тока конвекции и возмущение ИП определяется как сумма вклада всех облачных генераторов и конвективного генератора фconv (Ru):

ф(Ru) = т" J -rdV-т = E Ф C^loud (Ru)+Ф^conv (Ru).

^u 4π_VC σ(r)r²i ^{i u u}

Моделирование конвективных токов показало, что они наиболее существенны в неустойчивых пограничных слоях. Для представления турбулентного конвективного тока в неустойчивом пограничном слое используем, следуя работе [Willett, 1979], процедуру замыкания уравнений второго порядка. Результаты численных расчетов показывают, что плотность конвективного тока является плавной функцией высоты с максимумом jcmax на высоте z<0.1H. Высота и интенсивность максимума возрастают с ростом параметров R и H/L. Согласно [Willett, 1979], плотность конвективного тока jc пропорциональна плотности полного тока J и может быть записана в виде jc=JF(z/H; Н/L; R). В свою очередь, J определяется ИП: J=φi/R∞, R∞=Ru+RL=2·1017 Ом·м2 (RL=H/[λ] – сопротивление пограничного слоя, Ru – сопротивление оставшейся части атмосферного столба воздуха), и не зависит от интенсивности конвекции. Последние исследования [Kulkarni, 2009] не изменили в значительной степени этой оценки. Принимая во внимание в (6) токи, обусловленные деятельностью грозовых/ливневых облаков и конвективного генератора, находим, что ИП определяется интегральным соотношением вида

^ϕi⁼

1     j_rdr

4n J о( r) r²

^ 'Lcloud

i

₊ ϕi   1

R∞ SEσ0

и SJSE^O.4. В этом случае фi = 1.1^ Lcloud , т. е. кон- i вективный генератор увеличивает ИП на 11 %. При более благоприятных значениях проводимости, толщины пограничного слоя и параметра F ИП может увеличиться за счет конвекции на 25 %.

Итак, благодаря конвекции потенциал ГЭЦ повышается. Этот эффект особенно важен потому, что суточное перемещение области конвекции по поверхности Земли может быть причиной регулярных вариаций в суточной вариации ИП, усиливающих вклад грозовых генераторов.

Численные расчеты

Для иллюстрации приведем численные расчеты. Считалось, что ИП в отсутствие конвективного генератора формируется благодаря току облаков средней плотности Jext=4·10–6 CГС, который рас- пределен по всей области (r, θ)∈ [r–, r+][–π/9, π/9].

Конвективный ток со средней плотностью Jext=1.5·10^–6 CГС распределен в областях

В итоге выражение для ИП приводится к виду

(r, θ)∈[r_E, r]

π

, а, Г -1 П 2П и ⁽г, 9) е[ rE, r ] 9,-

Ф,.= X Lc^м

i

-1

S^-H-F 1 , sE R^0 J

слое толщиной r=1 км; r–=rE+5 км, r+=rE+10 км, rE=6 км. Для проводимости было взято простейшее ( Г — ^rF 1

выражение   o( r, 9) = o0 exp II. Результаты где Lciloud – суммарный вклад в ИП генераторов, связанных с грозовыми и слоисто-дождевыми облаками, σ0 – проводимость атмосферы на нижней границе области, занятой сторонними токами, Sс – площадь этой области, SE – площадь поверхности Земли, R∞ – сопротивление столба атмосферы с единичной площадью, H – высота пограничного слоя, F – безразмерный коэффициент, возникающий в теории турбулентности погранслоя, меняющийся от 1 до 1.5. Полученные формулы справедливы для произвольных соотношений между линейными размерами заряженной области облака и высотой h и могут быть использованы, в частности, для численных расчетов ИП в климатических моделях. Для оценок использованы значения: R∞=2·1017 Ом·м2; σ0=2·10–14 Ом–1·м–1; H=1 км, F=1

численных расчетов представлены на рис. 2 и 3. Видно, что ИП, равный в отсутствие конвективного генератора 200 кВ, повышается на 20 % и приобретает значение, близкое к наблюдаемому.

Выводы

Аналитическое выражение для вклада локализованных токов в ионосферный потенциал позволило сделать корректную оценку вклада глобально распределенных конвективных токов . Полученное выражение показало, что конвекция усиливает вклад таких источников, как грозовые/ливневые облака, и величина этого усиления варьирует от 10 до 20 % в зависимости от площади, охваченной интенсивной конвекцией, средней толщины пограничного слоя и сопротивления воздушного столба в отсутствие конвекции .

Рис. 2. Электрический потенциал над полюсами без учета и с учетом конвективного генератора.

Рис. 3. Электрический потенциал над экватором без учета и с учетом конвективного генератора (КГ).

Выдвинута гипотеза о том, что суточные изменения площади конвекции на земной поверхности могут быть причиной регулярных изменений в суточной вариации ионосферного потенциала, усиливающих вклад грозовых генераторов.

Работа поддержана грантом РФФИ № 11-05-12055-офи-м-2011, программой Президиума РАН № 4 и мегагрантом Правительства РФ (договор № 11.G34.31.0048 ННГУ с Министерством образования и науки Российской Федерации).