О спектральных свойствах семейства дифференциального оператора четного порядка с суммируемым потенциалом

DOI:

1. Постановка задачи. Исторический обзор

Изучим спектральные свойства дифференциального оператора, задаваемого дифференциальным уравнением десятого порядка

y(10)(x) + q(x)• y(x) = X • a10 • y(x),0 < x < п,a > 0,                        (1)

с разделенными граничными условиями вида

y ⁽ m ¹ ) ( 0 ) = y ⁽ m ² ) ( 0 ) = ... = y ⁽ m ⁵ ) ( 0 ) = y ⁽ n ¹ ) ( п ) = y ⁽ n ² ) ( п ) = ... = y ⁽ n ⁵ ) ( п ) = 0, m 1 <  m ₂ < ... <  m ₅; n 1 <  n ₂ <  ... <  n ₅; m k , n k e { 0,1,2,....,9 } , k = 1,2,...,5.

Мы предполагаем, что функция q ( x ) является суммируемой на отрезке [ 0; п ] :

q (x) e L1 [0; п] о

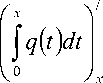
= q ⁽ x )

почти для всех x из отрезка [ 0; п ] .

В уравнении (1) число X _e C — спектральный параметр, функция q ( x ) - потенциал, функция р ( x ) = a ¹⁰ = const при x e [ 0; п ] - весовая функция.

В работе [16] был изучен дифференциальный оператор четного порядка 2 m вида

(-1)my(2m)(x)+ p(x)• y(x) = X- p(x),0 < x < п,                      (0.1)

y (0) = y(2) (0) =... = y(2 m - 2)(0) = y (п) = y (2) (п) =... = y(2 m - 2) (п) = 0,            (0.2)

был вычислен регуляризованный след этого оператора, при этом потенциал p ( x ) предполагался гладкой (бесконечно дифференцируемой) функцией на отрезке [ 0; п ] . Граничные условия (0.2) – специального вида: половина граничных условий берется в левой точке отрезка, половина – в правой точке отрезка. В изучаемом нами операторе (1)–(2) с условием (3) суммируемости потенциала q ( x ) граничные условия (2) такого же рода, только мы изучаем сразу целое семейство дифференциальных операторов: граничные условия зависят от параметров m 1 ,m ₂,..., m 5 ; n 1 ,n ₂,..., n 5 ; m k , n k e { 0,1,2,....,9 } , k = 1,2,...,5.

В работе [16] также упомянут следующий факт: если функция p ( x ) суммируема на отрезке, то асимптотическая формула для собственных значений оператора (0.1)–(0.2) имеет следующий вид: X n = n ^{2 m} + O (1), этой точности не хватает для вычисления регуляризованных следов. Цель нашей статьи – выписать более точные асимптотические формулы для собственных значений в случае суммируемого потенциала, то есть разложить величину O (1) по степеням числа n .

В дальнейшем делались попытки уменьшить гладкость коэффициентов уравнений, задающих дифференциальный оператор (в основном для операторов второго порядка): в работе [3] изучалась сходимость разложений по собственным функциям в точках разрыва коэффициентов дифференциального оператора, в работе [5] исследовалась точная зависимость между асимптотическими разложениями собственных значений краевых задач Штурма – Лиувилля и гладкостью потенциала. В работе [18] изучена обратная задача на собственные значения для оператора Штурма – Лиувилля с разрывными коэффициентами. В работе [17] приведены примеры изоспектральных операторов второго и четвертого порядков с разрывными коэффициентами (обратная задача для таких порядков не имеет единственного решения).

В работе [12] автором вычислены формулы регуляризованных следов для операторов второго порядка с разрывными коэффициентами. В работе [13] тот же вопрос решен для функционально-дифференциального оператора с разрывным потенциалом. В работе [8] были изучены некоторые спектральные свойства дифференциальных операторов второго порядка с разрывной весовой функцией, как и в работе [17] были приведены некоторые примеры изоспектральных операторов.

Дальнейшее уменьшение гладкости коэффициентов привело к изучению операторов с суммируемыми коэффициентами. В работе [2] найдена асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма – Лиувилля на отрезке с суммируемым потенциалом. В работах [7] и [11] автором продемонстрирован метод, отличный от метода работы [2], для изучения операторов с суммируемыми коэффициентами, порядок которых выше второго (четвертый в работе [7], шестой в работе [11]). В работе [10] изучены спектральные свойства дифференциальных операторов произвольного нечетного порядка с суммируемым потенциалом, граничные условия которого имеют конкретный вид типа (0.2).

• 2.    Асимптотика решений дифференциального уравнения (1) при больших значениях спектрального параметра λ

Пусть X = 5 ¹⁰, 5 = 1^Х , при этом выберем ту ветвь арифметического корня, для которой 10 1 = + 1 . Обозначим через w_k ( к = 1,2,...,10 ) различные корни десятой степени из единицы:

2пi(к j)                                           2пi                 х             Э А w10 = 1, w, = e10    , к = 1,2,...,10; w = 1; w2 = e10 = cos — + i sin — = z2; w4 = z3;...; wD = zp-1;

• ^{k k                            1      2}               ( 10 J 1 10 J                     p (4)

W p + 10 = W p ; p = 1,2,...,10.

Числа w_k ( к = 1,2,...,10 ) из (4) делят (1) единичную окружность на десять равных частей:

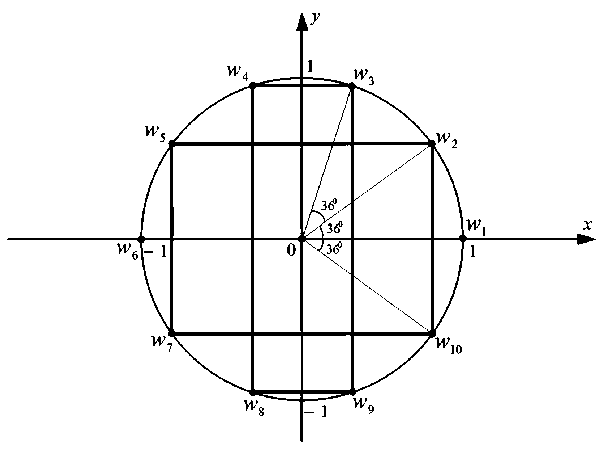
Рис. 1

При этом имеем: w 1 = w 1 = 1; w ₁₀ = w₂; w₉ = w ₃; w₈ = w 4 ; w₇ = w₅; w ₆ = w ₆ = - 1;

Im(w6 ) = Im(w1 ) = 0; Im(w5 ) = Im( w2); Im(w4 ) = Im(w3); Im(w7 ) = Im(w10 ) = - Im( w2);

Im(w8) = Im(w9) = - Im(w3).

Для чисел wk(k = 1,2,...,10) из (4) и рисунка 1 справедливы следующие соотношения: 1010

£ w = 0, p = 1,2,...,9; £ wP = 10, p = 0, p = 10.

k=1

Методами работ [6, гл. 2; 7; 10; 14, гл. 2] устанавливается теорема.

Теорема 1. Общее решение дифференциального уравнения (1) имеет вид: 1010

y(x,5)=£Ck • Ук(x,5)y(m)(x,5)=£Ck • ykm)(x,5)m = U,...,9, к=1

где

C k ( k = 1,2,..,10 ) – произвольные постоянные, при этом фундаментальная система

решений ^{ y k ⁽ x , ^{5 )} } k °₌₁

подчиняется следующим асимптотическим оценкам:

Im s ax

■y k ⁽ x , ⁵ ) = ^- , . ' ^⁺ O ^f e^)^k = 1,2.....¹⁰;

^{y k}m ^{) (} X , ⁵ ) = w m e mk

(a5)

awk sx

^“

A 9m^{k (} x , ⁵ ) + 0

1 n 9 9    ' —

10 a ⁹ s ⁹

Im s ax e ¹

к 5

, k = 1,2,...,10; m = 1,2,...,9;

xxx

A 9, _k ( x , 5 ) = w 1 e ^aw 1 ^5X J q ( t ) e ^{a (} w^{k -} w ¹ ) ^5t dt + w ₂ e aw^5X J q ( t ) e ^{a (} w^{k - w 2} ) ^5t dt + ... + w ₁₀ e aw ^{10 5x} J q ( t ) e ^{a (} w^{k -} w ¹⁰ ) ^5t dt ; (₉)

A 9 mk ( x , 5 ) = £ w p w m e ^aw^p5x J q ( t ) e a ⁽ w^{k -} w^p ) ⁵t dt , k = 1,2,...10 p = 1,2,...9.

p=10

При выводе формул (6)–(10) мы использовали соотношения (5) и требовали выполнения следующих начальных условий:

A 9 , k ( 0, 5 ) = 0; A 9mkk ( 0, 5 ) = 0; y_k ( 0, 5 ) = 1, y k^m ) ( 0, 5 ) = ( a5 ) ^m w m ; k = 1,2,...,10; m = 1,2,...,9. (11)

• 3.    Изучение граничных условий (2)

Подставляя формулы (6)–(11) в граничные условия (2), имеем:

10                                  10

У(m )(0, s ) = 0 «X Ck' У»"" )(0, s ) = 0 «X Ck •(as)"' ' W^p = °;

k = 1                                    k = 1

J2)

У p \п, s ) = 0 « X C k • Ук p ( n , s ) = °; p = 1,2,...,5.

k = 1

Система (12) – система из десяти линейных однородных уравнений с десятью неизвестными C ₁, C ₂,..., C ₁₀ . По теореме Кронеккера – Капелли, такая система имеет ненулевые решения только в том случае, когда ее определитель равен нулю. Поэтому справедливо следующее утверждение.

Теорема 2. Уравнение на собственные значения дифференциального оператора (1)–(3) имеет следующий вид:

	w 1 m 1	w 2 m 1        ..	.       w 9 m 1	w 1 m 0 1
	w 1 m 2	w 2 m 2        ..	.       w 9 m 2	w 1 m 0 2
f ( s ) =	... w 1 m 5 y ( ” 1 )( П s )	...             .. w 2 m 5        .. У 2 ” 1 )( n s )    .	.             ... .       w 9 m 5 .    У 9 ” 1 )( n s )	... w 1 m 0 5 У 1О 1 ) (n , s )		= 0.	(13)
	y ( ” 2 )( n s )	У 2 ” 2 )( n s ) .	. У 9 ” 2 ) ( п s )	»!; ■	(п, s )
	y f ” 5 ) ( n , s )	...             .. У 2 ” 5 )( n s )    .	.             ... .    У 9 ” 5 ) ( п s )	у 10 5	(к, s )

Используя теорему Лапласа, разложим определитель f ( s ) из (13) по последним пяти строчкам:

f ^{( s} ) R 1,2,3,4,5 ( ^П , ^s - ... + R 6,7,8,9,10 ^(п , ^s

•D -R

D 6,7,...,10     R 2,3,4,5

• D 1,2,.,5 + ^R 1,3,4,5,6

5 ( ^П , s ) • ^D 1,7,8,9,10 + ^R 3,4,5,6,7 ^п , ^s ) • D 2,7,8,9,10 - ... = ⁰,

^(п , ^s ) • D 1,2,8,9,10

-

где введены обозначения:

R j^j ^(П , ^s )

У j” ^)(п , ^s )    У ( ” 1 ⁾⁽ⁿ , ^s ) ...

Уj2)(n,s)   У(n2)(n,s)

...                   ......

у(П5)(n,s)   у(П5)(n,s)

У I”1 )(n,s) у (П2 )(п,s)

У j” 5 * ( ” . s )

w ^{m 1}

w ^{m 1}

w ^{m 1}

D

w m 2

w m 2

w m 2

€

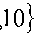
w m

wm 5

w m

В силу удобной нумерации чисел w_k можно вывести рекуррентные формулы.

Для определителя D _1,2,3,4,5 имеем:

из (4) для алгебраических миноров D _{, ,...,} из (16)

	m w 1 m 1	m w 2 1     .	m ..    w 5 1		1 m 1	m z 1 .	4 m .. z 1
D 1,2,3,4,5 =	m w 1 2 ...	m w 2 2    . ...       .	m ..    w 5 2 ..      ...	( 4 )	1 m 2 ...	m z 2     . ...       .	4 m .. z 2 ..       ...
	m w 1 m 5	m w 2 5     .	m ..    w 5 5		1 m 5	m z 5      .	4 m .. z 5

П ( z m k — z m ) = D 5 * 0, k >  p k , p = 1,2,3,4,5

так как D _1,2,3,4,5 представляет собой определитель Вандермонда чисел z ^{m 1} , z ^{m 2} ,..., z ^{m 5}. Далее находим:

D 2,3,4,5,6

w ₂ ^{m 1}

w 2 ^{m 2}

w ₃ ^{m 1} w 3 ^{m 2}

w ₆ m 1     z m 1    z 2 m 1

w m 2 ( 4 ) z m 2    z ² m 2

5 m z 5 m 1

5 m z 5 m 2

m 1     m 2           m 5

^{z z} \"7 ^z     '^Ly1,2,3,4,5

^{( 19 )} M

= Z M ⁵ • D 5 ,

m w 2 ⁵

m w 3 ⁵

m w 6 ⁵

m z m ₅

2 m z m ₅

5 m z 5 m ₅

^M 5 = E m k .

k = 1

Аналогичным образом получаем:

D       ~z ² M5.D D        = z^{( k - 1 ) M} 5 D £ = 12   6' D

^3,4,5,6,7     ^z       ^5 ; ^k , k + 1,..., k + 4     ^z          ^5 ,^   ¹ ,^,...,6; ^7,8,9,10,11     ⁽   )) ^1,7,8,9,10

( - 1 ) - z ^{6 M 5}

• D. , D,    ,    ,

^{5       j} к + 10 , j m ,..., j p

= ^Dh ,j m ,..j p ; D k , k + 1.... k + 4 = ⁽ - 1 ) k ^{- 1} • z ⁽ k ^{- 1 ) M 5} • D 5 , ^k = ^7,8,9,10.

Подставляя формулы (15) в формулы (7), (8), разложим определитель R столбцам на сумму определителей, получим:

( n , s ) по

R

⁽ⁿ , ^ ) = R

⁽ⁿ , ^ )

R

^^ J 1 , j 2 ^,...^, j 5 , ^{k - 1}

k = 1

—

10 a ⁹ s ⁹

⁽ⁿ , ^s )

---+ O

< e ,m ^s ^.)

к

s ¹⁸

; j , , j 2 ,..., j 5 e { 1.2....^0 } . ⁽²⁰⁾

R

( n ^s ) =

w m 1 j 1	aw e j 1	п s	w m 1 j 2	aw e j 2	п s .	..    w m 1 j 5
w m 2 j 1	aw e j 1	п s	w m 2 j 2	aw e j 2	п s .	..   w m 2 j 5
w m 5 j 1	... aw e j 1	п s	w m 5 j 2	... aw e j 2	. п s .	.. ..   w m 5 j 5

...

aw zc ns e j5

aw ej eaw

П s

n s

,

определители R

( n , s ) получаются из определителя R

1   2       5                                                                                             * 1   2       5

( k = 1,2,3,4,5 ) на столбец ⁽ A )” ¹ j k ( л , s ) A gA ( п , s ); ...; A g ” ⁵ j k ( п , s ) ) .

Основное приближение уравнения (14)–(16) получается из уравнения

( n , s ) заменой k -го столбца

f ) ^{( s} ) = ^R 1,2,...,5,0 ^(п , ^s ) • ^D 6,7,8,9,10

—

^R 2,3,...,6,0 ( ^П , ^s ) • ^D 1,7,8,9,10 ⁺ ... = ⁰,

где определители R

( п , s ) определены по формуле (21), при этом имеем:

R

( п , s ) = e

^a E wjk ^{п $}

, k = 1

m w j ₁ ¹ w ^mj ²

m w j ₂ ¹ w ^mj ²

.

.

.

.

.

.

m w j ₅ ¹ w ^mj ²

.

...

m wmj 5

...

m wmj 5

.

.

.

.

.

.

...

m wmj 5

Для нахождения асимптотики корней уравнения (14)–(16) сначала необходимо найти асимптотику корней уравнения (22), а для этого необходимо изучить так называемую индикаторную диаг-

рамму уравнения f 0(5) = 0, (см.: [1, гл. 12]), то есть необходимо исследовать выпуклую оболочку показателей экспонент, входящих в уравнение (22), с учетом формулы (23). Таким образом, нам

Е wj_k ; j j 2,-, j 5 е { 1,2,...д⁰ } > . к = 1

необходимо построить выпуклую оболочку множества точек

• 4.    Изучение индикаторной диаграммы уравнения (22)

Начнем изучение выпуклой оболочки множества точек {w. + w. ;j, j,..., j e {1,2,...,10}}. Точки wk (k = 1,2,...,10) из (4) делят единичную окружность на десять равных частей, они изображены на рисунке 1 и при этом расположены симметричным образом: есть симметрия относи- тельно точки О(0,0) и относительно координатных осей. Из правила параллелограмма сложения векторов и геометрических соображений следует, что индикаторная диаграмма уравнения (22) имеет следующий вид (N = 5, на рисунке должно быть пять окружностей):

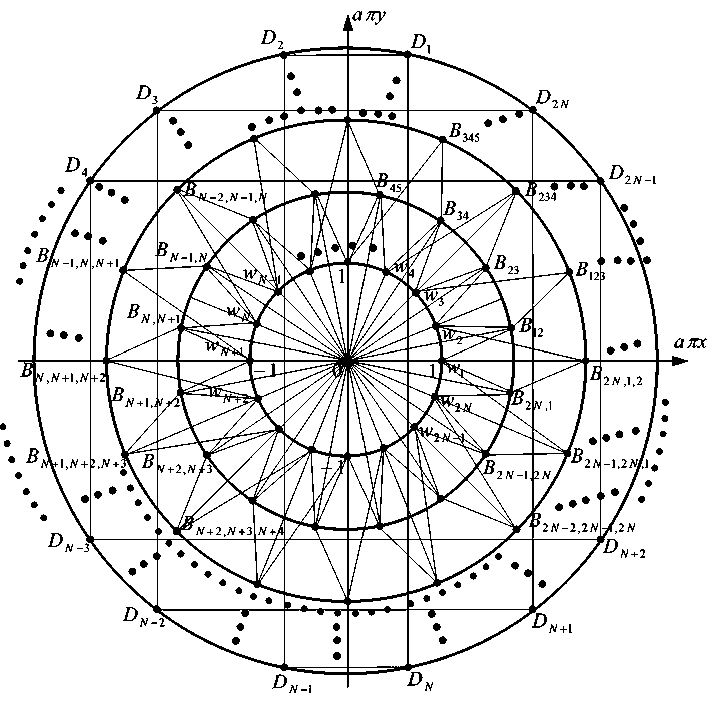
Рис. 2

На рисунке 2 точка B12 соответствует числу w1 + w2 (а также сумме векторов Ow1 + Ow2), точка B23 соответствует числу w2 + w3 (и сумме векторов Ow2 + Ow3), точка Bmk соответству ет числу wm + wk (и сумме векторов Owm + Owk), точка Bkn соответствует числу wm + wk + wn

(и сумме векторов Owm + Owk + Own), m, k, n = 1,2,...,2N. Несложно доказать следующее неравенство: w + w4| < w + w3| < w + w3|, |w2 + w5| < |w2 + w4| < |w2 + w3|,.... Действительно, складывая векторы, видим, что

OB₁₄ <  OB₁₃ <  OB₁₂

OB 25

< OB 24

< OB ₂₃

, при этом

OB₁₂ - OB ₂₃ - OB 34

OB, l2

2 n - 1,2 n

^{- OB} 2 n ,1 . Значит, точки B₁₂,B₂₃,B 3

^B 2 n - 1,2 n , ^B 2 n ,1 ле ^-

жат на окружности радиуса R - OB₁₂ >  1 и делят эту окружность на десять равных частей,

точки B 13 , B 14 , B 24 , B 25

,...

, B + m , . ( m - 2,3

8 8; к - 1,2,...,10 ) попадают внутрь этой окружности, так

как | w_{m + k} + w_k | < | w_{k + 1} + w_k | при m - 2,3,...,8 . Этот факт доказывается и аналитически:

| wk + 1 ⁺ w k | ^-

2ni ,        2 n i/, k --(k-1)

e ¹⁰ + e ¹⁰

e

•

2 n i 1

— e10 2 + e

- 1 • 2 • cos —

I 10

f n 1 - 2cos — ,

1 10 J ,

| w k + m ⁺ w k | ^-

2 n i/,       . x        2 n i ,

(k+m-1)      --k e10        + e10

e

•

2 п i m

— e10 2 + e

, , f n m i     f n m i       f n

- 1 • 2 • cos — , cos — <  cos —

I 10 J    I 10 J      1 10

при m - 2,3,...,8 , это означает, что | w_{m + k} + w_k | < | w_{k + 1} + w_k | при m - 2,3. что выпуклой оболочкой множества точек { w j + w^ , j₁, j ₂ - 1,2,...,10 }

,...

,8 . Значит, мы доказали,

является правильный де-

сятиугольник B 12 B 23 B 34 ... B 9,10 B 10,1 .

Аналогичным образом доказываем, что выпуклой оболочкой множества точек { w j + W j^ + W j^ , j₁, j ₂, j ₃ - 1,2,...,10 } является изображенный на рисунке 2 правильный десятиугольник B ₁₂₃ B ₂₃₄ B ₃₄₅... B ₈ , ₉ , ₁₀ B^ ₎ , ₁₀ , ₁ B ₁₀₁ , ₂ , где точка B_kmn соответствует сумме w_k + w_m + w n (а также сумме векторов Ow , + Ow + Ow ), все точки лежат на окружности радиуса kmn

R ₁ - OB ₁₂₃| >  OB 12J >  1. На границах этого многоугольника лежат точки w ₃ + w ₂ + w ₃ , w ₂ + w ₃ + w ₄ , w ₃ + w ₄ + w ₅ ,^, w ₈ + w ₉ + w ₁₀ , w ₉ + w ₁₀ + w ₃ , w ₁₀ + w ₃ + w ₂ , точки w ^ + w ₂ + w ₄ , w ₁ + w ₂ + w ₅ , w ₁ + w ₃ + w ₄ ,^ (у которых сумма индексов суммирования больше единицы) попадают внутрь этого десятиугольника и на индикаторную диаграмму не влияют.

Аналогичным образом устанавливается, что выпуклой оболочкой множества ^{{ w} j . ^{+ w} j 2 ^{+ w} j 3 ^{+ w} j 4 , Ь ^j 2 , ^j 3 , ^j 4 ^{- 1,2,}...^{,10 }} является десятиугольник ^4 B 2345 B 3456 ... B 9,10,1,2 ^B _w,1,2,3 , где B_mknp соответствует сумме w m + w_k + w n + w p ;...; выпуклой оболочкой множеств а

k ⁺ w ⁺ ... ⁺ j j^j 2

,...,

j ₅ - 1,2,...,10 } является десятиугольник D₁D ₂... D ₁₀ , где точка D m ( m - 1,2,...,10 )

соответствует сумме ^ ^w m + k - 1 , если ввести обозначение w_{n + 10} - w_n , n - 1,2,

...

I ^{k 1}

множества wj- + wj- + ... + w₂ , ]„ j ₂

,10 . Остальные точки

,...,

j ₅ - 1,2,...,10 } попадают внутрь многоугольник а

D 1 D 2 ... D 10 и на асимптотику корней уравнений (22)–(23) и (14)–(16) не влияют .

Из общей теории нахождения корней квазиполиномов вида f ( 5 ) из (14)-(16) следует (см.: [1, гл. 12]), что собственные значения дифференциального оператора (1)–(2)–(3) находятся в секторах T ₁, T ₂ ,..., T ₁₀ бесконечно малого раствора, биссектрисы которых являются серединными перпендикулярами к отрезкам [ D ₁ ; D ₂ ][ D ₂ ; D ₃ ], ..., [ D 9 ; D ₁₀ ][ D ₁₀ ; D ₁ ] соответственно.

5. Асимптотика собственных значений в секторе T ₁

Исследуем подробно асимптотику корней уравнения (14)–(16) в секторе T ₁, биссектриса которого перпендикулярна отрезку [ D ₄; D 5 ] . В формулы (14)-(16) необходимо подставить формулы (17)–(19) с учетом формул (20)–(21), в которых надо учесть формулы (7)–(11) и оставить в получившемся уравнении только те экспоненты, показатели которых задаются точками, комплексно-сопряженными к точкам D ₄ и D ₅ , то есть точками D ₁ и D ₂ . Поэтому верно следующее утверждение.

Теорема 3. В секторе T ₁ индикаторной диаграммы (рис. 2) уравнение на собственные значения дифференциального оператора (1)–(2)–(3) имеет следующий вид:

g 1 ^{( 5 )- R} 1,2,3,4,5 ^(п) " ^D 6,7,8,9,10 ^{- R} 2,3,4,5,6 ^(п) " ^D 1,7,8,9,10 ^- 0 .                       ⁽²⁴⁾

Из формул (17)–(18) следует, что

D 6,78,910 = z 5 M ⁵ • D 5 , D 178910 = z 6 M ⁵ • D 5 , D 5 * 0.                       (25)

Применяя формулы (25) и формулы (20) (21) для сектора T ₁ уравнение (24) можно переписать в следующем виде:

g 1 ⁽ s ) =

E ^R 1,2,_..,5,k ,9 ^(п , ^s )       / 1 \

R i 2 5 n ( п , s ) — k = 1 ------+ О -

^1,2,-^,5,0V    ’         10 a⁹ s⁹          4 s¹⁸)

^R 2,3,...,6,0 ^(п , ^S )

E ^R 2,3,--,6, k ,9 ^(П , ^S )

k =1 ________________________

10 a ⁹ s ⁹

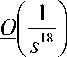
• z

^{5 M 5} • D ₅

• z ^{5 M} 5 • D ₅ = 0.

—

В уравнении (26) поделим на z ^{5 M 5} • D ₅ * 0 , а для величин R 1, ₂ ,..., ₅ , ₀ ( п , s ) и R ₂ , ₃ ,..., ₆ , ₀ ( п , s ) применим формулы (21) и (23):

5                                                     6 5

a E w k -m                 , _х ^a E w k '^{п s}         P        —

^R 1,2,...,5,0 ^(п , ^s ) = e = ¹       • ^R 5 , ^R 2,3,...,6,0 ^(п , ^s ) = e k = 2       • ^R 5 • z 5 , ^P 5 = E n k ,

k = 1

R 5

n w 1 ^{n 1}

n w 1 ^{n 2}

n w 2 ^{n 1}

n w 2 ^{n 2}

w ₅ ^{n 1}      1 ^{n 1}     z ^{n 1}

w ₅ n 2 ( 4 ) 1 "²     z" ²

4n z1

n w 1 ^{n 5}

n w 2 ^{n 5}

n w 5 ^{n 5}

nn

1 ⁵ z ⁵

z ⁴ " 2 ⁽ = )   n ( z

...       k > p

4 n       k , P = 1,2,...,5

z ⁵

— z " ) = R 5 * 0.

С помощью формул (27), (28) уравнение (26) можно переписать в следующем виде:

g 1(s ) =

—

где величины

a E W k n s e ^k = '

—

M _p a ^E wk ^{п s} z ⁵ • z ⁵ • e k = ²

E R 2,3 6,10, k ( n , s ) • z ^M 5

k = 1

R 1,2,...,5,9, k

—

10 a ⁹ s ⁹ • R ₅

+ ОI ^18 ] = 0

• ^{E R} 1,2,...,5,9, k ^(п , ^{s ) —} k = 1

( п , s ) получаются из определителя R i,₂,...,₅,₀ ( п , s ) из (21) заменой k -го стол

бца на столбец ( A 9"k ( п , s ); A 9 " ² _k ( п , s ); ...; A 9 ' ⁵ _k ( п , s ) ) . Выпишем некоторые из этих величин:

A9'1(п, s ) w"1 eaw 2s п   . ..   w" 1 eaw 5 s п А1,2,...,5,9,1(п, s ) = A9',1 (п, s ) ... w" 2 eaw 2s п   . ...            . ..   w" 2 eaw 5 s п ..           ... A9',1 (п,s ) w"5 eaw 2 s п   . ..   w" 5 eaw 5 s п w", eaw, ^п w5n1e

^A 1,2,...,5,9,2 ^(п , ^s ) =

w " 2 e aw i ^{s п}

A 92 ( п , s ) w ₃ " ¹ e ^{aw 3} ' ^п

A 9 ⁿ , ² ₂ ( п , s ) w ₃ " ² e ^{aw 3} ' ^п

aw 5 s п

w 5 n 2 e

aw 5 s п

w n ⁵ e ^aw 1 ' ^п    A 9 " , 5 ₂ ( п , s ) w n N e aw ³ ' ^п

w 5 n 5 e

aw 5 s п

^A 2,3,...,6,9,1 ( ^П , ⁵ )

A 9'12 (п , 5 )	n । aw-xS п w 3 1 e 3       .	n ..    w 6 1
A 9',2 ( п , 5 )	aw 5 п w 3 2 e 3      .	n ..   w 6
... A 9 ' , 5 2 (п , 5 )	...            . aw 5 п w 3 5 e 3      .	.. n ..    w 6 5

...

■ 2 e ^aw 6 ^{5 п}

11 e ^aw 6 ^{5 п}

,...

15 e ^aw 6 ^{5 п}

Используя формулы (9), (10), из (30) находим, применяя свойства определителей:

,     ,              a Z w_k п 5

^R 1,2,...,5,9,1 ^{( n} , ⁵ ) = w 1 ^R 5 e k = 1

п

* I ...

a Z w_t п 5 — w ₆ R ₅ z ^⁵ e ^k = ²

п

п

( п

V ⁰ V a 11

V 0

...       ; J ...

[ w p ^— w r ) ⁵t dt

^a Z ^wk ^{п 5}

^R 1,2,...,5,9, k ^(п , ⁵ ) = w k * ^R 5 * e k = '

(п

•I-

^V a 1,6 ^{V 0}    7 apr

A

V 0

^V apr

;(31)

.

, k = 2,3,4,5;

R 2,3,...,6,9, k ^(п , ⁵ ) = w k + 1 * R 5 * ^z P

a Z wr П 5

* e k=2

V ⁰

(п

*I

V ⁰

^V akk

.

.

.

, k = 1,2,3,4;

^V a , k + 1, k + 1

a Z w_k п х

^R 2,3,...,6,9,5 ^(п , ⁵ ) = ^— w 1 * ^R 5 * e k = 1

(п

* I ...

V0 .

P ^a Z wk ^{п 5}

+ w ₆ * R ₅ * z P * e k = ²

/ a ,6,1

f ^п

*I--I

V ⁰ V a ,6,6

.

Заметим, что в формулах (31)–(34)

имеем:

π

π

π

I ...      = J ...      = I ...

V 0   V a 11

V 0   V a 22

V 0 V akk

π

= J q ( t X 11 , k = 1,2,...,10.

Подставляя формулы (31)–(35) в уравнение (29), поделим на следующему более удобному для изучения виду:

e ^a k ^z ₂ w k ^{п 5} , преобразуем

его к

g 1 ( 5 ) = [ e ^a ' "'

— w 6 ) 5 п

—

M z 5 * z

P 5 ]— ¹

10 a ⁹ s ⁹

*

п

I ...

V0 .

a ( w, * e ^{( 1}

V a 11

— w ₆ ) 5 п X ¹

6) *Z wk k =1

п

—

MP z 5 * z 5

•^

V ⁰

V a 22

•

*Z wk + w1 *z k=2

M 5

п

*p

V ⁰    V a ,6,1

* e ( w 1 — w 6 ) 5 п

—

P w6 * z5

(п A

* J ...

V ⁰ V a ,1,6 J

U Ol

Основное приближение уравнения (36) имеет вид:

e ⁽ w

2 п i         2 п i _P

w6)5п = zM5 * zP = e2 k * e10 5 * e 10 5 o 5k,1,осн

~

2 ik

a ( w 1

^

^w 6 )

~ M

, k = k + —5

P

+ —, k e N ,H7)

10         (37)

«осн» означает основное приближение, индекс 1 у величин s_{k ,1, осн} означает, что мы изучаем сектор Т ₁ индикаторной диаграммы (рис. 2).

Из общей теории (см.: [4; 15]) следует методика нахождения асимптотики корней квазиполиномов вида (36).

Теорема 4. Асимптотика собственных значений дифференциального оператора (1)–(2)–(3) в секторе Т ₁ индикаторной диаграммы (рис. 2) имеет следующий вид:

5k ,1 =   / a (w1

2 i

—

~

w)Ak +

d o z- 1     „( 1

—^{92 k 21} + O ---

~ ⁹    4 ~ ¹⁸

~ MP

, k = k + —5 + —,

10   10

k e N ; M ₅ = £ m k ; P 5 = £ n k . (38)

k = 1

k = 1

Вид асимптотики (38) показывает, что у оператора (1)–(2)–(3) невозможен эффект «расщепления» собственных значений, изученный автором в работе [9].

Для доказательства теоремы 4 необходимо доказать, что в формуле (38) коэффициенты

d _{9, k ,1} находятся единственным образом и привести явные формулы для их вычисления.

Применяя формулы Маклорена, имеем:

e^{a (} w 1

^w * ’"I k, = ^{exp a} (

. w1— w6)пs •

2 i

a ( w 1

—

~

W J 1 ^{k +}

d 1

9, ^k ,1 + O

~ 9    4 ~ ¹⁸

MP

= z 5 • z 5 •

2пi • d9kl     ( 1 )

• 1 +--^t+ + O     .

k⁹      4 k ¹⁸ 7

Подставляя формулы (39) и (38) в уравнение (36), получаем:

MP  MP

z 5 • z 5+2пi • z 5 • z 5

•

^{2 п} i • ^d g £ I ( 1 9, ^k ,1 + O

~ 9      4 ~ ¹⁸

—

M z

5 • z

P 5

—

10 a ⁹

•

a ⁹ ( w 1

—

^w 6 ’ 9 г

2 i

i

•

1!          !1

• kк1+O к k

•

z

M 5

• z

•^; 1 + O I

+

a 11

•Е wn n=1

—z

M 5

• z

P 5

( п J ...

к 0

a 22

•Е wn n=2

+

MMP

w1 • z 5 • z 5 • z 5

п

J. .

к 0

\

—

^w 6 • z M ⁵

•z

MP

5 • z 5

⁷ a ,6,1

s k ,1

J - к0 .

\

7 a ,1,6

Приравнивая в этой формуле коэффициенты при k ~ ₉ , находим:

d

_ 1 (w1—w6 )9 — ---- • ------------

9, k ,1     2 π

10 • 2 9

• <

Е wn n =1

π

• J...

к 0    7 a 11

^— Е w n n = 2

π

• J...

к 0   7 a 22 J i

+

—

— M, ^w 6 • z ⁵

π

• J... I к0   7a,1,6

s k ,1, осн _ 2

.

В силу формулы (35) имеем:

1 1

1 + OI       I.

4 k ¹⁸ 7

M

w1 • z 5

π

• J •■• к 0 7a,6,1

s k ,1, осн

—

л

л

π

Z wn • J...

—

n = 1

к 0

7 a 11

π

Е wn • I...

n = 2

к 0

7 a 22 J 1

π

= ( w 1 ^— w 6 ) ^ J q ( t ) dt .

Для скобки [, .. ] ₂ из (40) в силу формул (31), (37) и (4) I ^w 1 = 1, ^w 6 = ¹ I получаем:

ц =

M z ^{M 5}

п

J ..

к0 .

Л

+ z ^{M 5}

⁷ a ,6,1

• ^dta ,6,1 L, s k ,1, осн

— — M.

+ e ¹⁰

s k ,1, осн

П

п

J ..

к ⁰ 7 a ,1,6

s k ,1, осн 2

⁵ J q ^{(t ) e}xp⁽2 k dt a_a ,1,6

s k ,1, осн

' ^п m

= e ¹⁰ 5

п

= 2 J q (t’

п

J q ^{( t} ’ exp a ⁽ w

—

W1 )•t •

2 ik

cos ^{2 kt —} 2 E ^M ₅ ^dt .

~

a ⁽ w 6

—

w 1 ’

•

Подставляя формулы (41) и (42) в (40), сделаем необходимые преобразования, получим:

d 9, k ,1

10 п

п                п

J q ⁽ t ) dt a ii + J q ^{( t} ) 00

cos

2 ~l ' M

~ dt к k = k +

M5 + P , x- i.

—⁵--- 5 ; k e N ; M,

10              5

= 2 m n ^; P = £ n k . (43) n = 1                n = 1

Формула (43) показывает, что коэффициенты d _{9, k ,1} формулы (38) найдены единственным образом, тем самым теорема 4 доказана.

Аналогичным образом изучаются секторы T ₂ , T ₃ ,..., T ₁₀ индикаторной диаграммы (рис. 2).

В результате получаем следующее утверждение.

Теорема 5. А) Асимптотика собственных значений дифференциального оператора (1)–(2)–(3) в секторе T ₂ индикаторной диаграммы (рис. 2) имеет следующий вид:

s k ,2 = / a ( w₂

2 i

—

w ) L

~

k +

d 1

9, ^k ,2 + O\

~ 9   4 ~¹⁸

~    M5 + P

, k = k + ⁵----5 ; k e N ;

,              ₁₀

d 9, k ,2

-1- .J

10п

п            п

J q (t) dt + J q (t)

cos

~

2 kt —

п M ₅

dt к k e N ,

(41)         2n тем самым справедлива формула s^ = s^ . e 10, k e N.

Б) В секторах T ₃, T ₄,..., T ₁₀ для асимптотики собственных значений дифференциального оператора (1)-(2) с условием (3) суммируемости потенциала q ( x ) справедливы следующие формулы:

2П           4П                 2П           6П                     2( m—1)П sk,3 = sk,2 • e10 = sk,1 • e10;sk,4=sk,3 • e10 = sk,1 • e10;-;sk,m = sk,1 • e 10 ;k e n,m = 1,2,...Д0.(46)

В) При этом имеем: X_k , _m = ( s_k , _m )⁰ , k e N , m = 1,2,3,...,10.      (47)

Формулы (38), (43)–(47) позволяют вычислить асимптотику собственных функций дифференциального оператора (1)–(2)–(3).

Теорема 6. Асимптотика собственных функций дифференциального оператора (1)–(2)–(3) может быть получена по следующей формуле:

m w1 1 m w2 1       ... m w9 1 m w101 m w1 2 m w2 2       ... m w9 2 m w102 y„ (x;sk,m ) = ... m w1m5 ...            ... m w2 5       ... ... m w9 5 ... m w105 y( n1 )(п, s ) y 2 n1 )(п, s)   ... y 9 n1 )(п, s) Ую )(п,s) y( n2 )(п, s ) y 2 n2 )(п, s)   ... y 9 n2 )(п,s ) y(n2 )(п,s) ... y( n4 )(п, s ) ...            ... y 2 n4 )(п, s)   ... ... y 9 n4 )(п,s) ... У10”4 )(п,s) y( n5)(x, s) y 2 n5)(x, s) ... y9 n5)(x,s ) У1(05)(x,s ) где вместо s подставляются sk,m из формул (38), (43), (46) для соответствующего сектора индикаторной диаграммы (рис. 2).