О степенном порядке роста нижних Q-гомеоморфизмов

Напомним некоторые определения. Следуя [1, разд. 9.2], k-мерной поверхностъю S в Rn называем произвольное iюпрерывное отображение S : ш ^ Rn. г,те ш — открытое множество в Rk := Rk U {то} 11 k = 1,...,n — 1. Функцией кратности поверхности S называем число прообразов

N (S, y) = card S 1(у) = card { x E ш : S (x) = у } , у E R n.

Другими словами, символ N(S,y) обозначает кратноеть накрытия точки у поверхностью S. Известно, что функция кратности является полунепрерывной снизу, и, значит, измерима относительно произвольной хаусдорфовой меры H^k (см. [1, разд. 9.2]).

Для борелевской функции р : Rn ^ [0, то] ее интеграл по поверхности S определя ется равенством

/ pdAk :=

S

Rn

р(у) N (S, у) dH^kу.

Пусть Г — еезжнетво k-мерных поверхностей S. Боре.тева функция р : Rn ^ [0 , то ] называется допустимой для семейства. Г. пи шут р E adm© если

У p^k dAk >  1

S для каждой поверхности S E Г. Пусть p E (1, то) — заданное фиксированное число. Тогда р-,модулем <семейства Г называется величина

Mp (Г) =

inf I pp(x) dm(x). ρ ∈ adm Γ

R ⁿ

Будем говорить, что свойство P имеет место для p-почти всех (р-п.в.) k-мерных по верхностей S семе Детва Г, если подсемейство всех поверхностей семейства, Г. для которых свойство P нарушается, имеет p-модуть путь.

Говорят (см. [1, разд. 9.2]), что измеримая по Лебегу функция р : Rn ^ [0, то ] является обобщение р-бопустихши для семейства, Г. состоящего из ( n - 1)-мериых поверхностей S в Rn. пи шут р Е ext p admR если

j р^{п 1} (х) dAn-i >  1

S

(1.1)

для р-п. в. S Е Г.

Пусть D ii D0 - облаети в Rn. n >  2. x₀ Е D. Q : D ^ (0, то ) - измеримая по Лебегу функция. Гомеоморфизм f : D ^ D' башем называть uuxcuuxi Q-гомеоморфизмом отиоситс.ионо р-лшбуля в точке xo, если

Mp У ^Sa) >   inf [ ^ dm(x)

pCextp adm X_A J Q(x)

A

(1.2)

для каждого кольца

A = A (xo, £1, £2) = {x Е R ⁿ : £1 < |х — xo| < £2} ,   0 < £1 6 £2 < d_o,

где do = dist(xo,dD), a Sa обозначает семейство всех сфер

S(x₀,r) = {х Е R ⁿ : |х — x₀1 = r} , r Е (£1,£2).

(1.3)

В работах [2] и [3] приводятся приложения нижних Q-гомеоморфизмов к исследованию локального и граничного поведения гомеоморфных решений с обобщенными производными и к задаче Дирихле для уравнений Бельтрами с вырождением.

Теория нижних Q-гомеоморфизмов применима к отображениям с конечным искажением класса Орлича - Соболева W^ при наличии условия Кальдерона и, в частности, к классам Соболева W Of щш р > n — 1 (см. [4-11]).

В данной работе мы устанавливаем аналоги леммы типа, Икомы - Шварца, для ниж них Q-гомеоморфизмов относительно р-моду.тя (см. [12. теорема, 2].

Ниже приведен критерий нижних Q-гомеоморфизмов относительно р-моду.тя при p>n — 1 (ем. [5. теорема. 3.7]). Впсрвью критерий был доказан при р = n в работе [13, теорема, 2.1] (см. также монографию [1, теорема, 9.2]).

Лемма 1.1. Пусть D — область в R ⁿ, n >  2, x₀ Е D. Предположим, что Q : D ^ (0, то) — измеримая фуикпня. Гомеоморфизм f : D ^ R ⁿ является нижним Q-гомсо-морфизмом в точке x₀ относительно р-модуля при р > n — 1 тогда и только тогда, когда

ε 2

Mp(fs  >/ й

ε 1

dr

-------,------, 0 6 £2 < do, n-i (xo,r)

p-n+1

(1.4)

где do = dist(xo,дD), Sr — семействеэ всех ссфер S(xo, г) = {х Е R ⁿ : | х — хо| = г}. Г Е (£1,£2). II

k Q k n-1 p-n+1

n-1

Q^p-n⁺ⁱ (х) dAn-i

S(x0,r)

)

p-n+1 n-1

.

(1.5)

Инфимум в (1.2) достигается только для функции

(       Q(x)      V^-n+1

(1.6)

^Р0(Х)      k Q k^-_ ( | x - xo l )

p-n +1

Замечание 1.1. Ниже мы используем стандартные соглашения, что a/то = 0 для a = то, a/0 = то, если a > 0, и 0 •то = 0 (см., например, [14]).

Пусть D - область в Rn ,n >  2. E,F С D - произвольные множества. Обозначим через A(E,F; D) семейство веех кривых y : [a,b] ^ Rn , которые соединяют E ii F в D, т. о. Y (a) € E, Y (b) € F и Y(t) € D при a

Следующая лемма, была, получена, в работе [10, лемма. 5.3].

Лемма 1.2. Пусть D и D 0 — области в Rn, n >  2. Предположим, что Q : D ^ (0, то) — измеримая по Лебегу функция и f : D ^ D' — нижний Q-гомеоморфизм в точке x_o относительно p-модуля при p > n — 1. Тогда имеет место оценка

_- n- 1 ε 2                           p-n +1

\ f                          l

A(fS1,fS2,fD)    6           -                ,          (1.7)

k Q k n-1 (xo,r)

ε₁        p-n +1

где Sj = S(xo, Ej). j = 1, 2, ii p-n+1

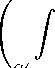
n-1               \ n ^{- 1}

Q^p-n+1 (x) dAn-i\       .                              (1.8)

,r)

ЗАМЕЧАНИЕ 1.2. Отметим, что норма ||Qk n- 1 (xo,r) по некоторым сферам S(xo,r) p-n +1

может быть равна бесконечности. По теореме Фубини функция kQk n-1 (xo,r) измерима но r в силу измеримости ио x функции Q. Более того.

ε 2

dr k Qk       (xo,r)

< то , 0 < E i <  E2 o,dD).                (1.9)

ε ₁        p-n +1

Это следует из условия гомеоморфности отображения f и леммы 1.2, поскольку —^ -емкость невырожденного кольца не може^ быть равна нулю. (Определение ^сти см. ниже.) Интеграл в (1.9) может быть равен нулю в случае, если k Q k n- 1 (x_o,r) = то p-n +1

и. в., но тогда, соотношение (1.7) очевидно.

• 2.    О емкости конденсатора

Следуя работе [15]. пару E = ( A,C). г де A с Rn - открытое множество и C -непустое компактное множество, содержащееся в A, называем конденсатором. Конден сатор E называется кольну вилi конденсатором, если G = A \ C - кольцо, т. с. если G - область, дополнение которой Rn \ G состоит в точности из двух компонент. Говорят так же. Tito конденсатор E = ( A,C ) лежит в области D. если A С D. Очевидно, что если f : D ^ Rn - непрерывное. отк_Г>ытос отображение ii E = ( A, C) - концеисатор в D. то ( fA,fC ) также коидеисатор в fD. Далее, f E = ( fA,fC).

Функция u : A ^ R абсолютно непрерывна на прямой, имеющей непустое пересечение с A, если она абсолютно непрерывна на любом отрезке этой прямой, заключенном в A. Функция u : A ^ R прииадлсжнт классу ACL ( абсолютно непрерывна па понта всех прямых), если она абсолютно непрерывна на почти всех прямых, параллельных любой координатной оси.

Обозначим через C0 ( A ) множество непрерывиых функций u : A ^ R¹ с компактным носителем. W0 ( E ) = W0(A,C ) - семейство неотрицательиых функций u : A ^ R¹ таких, что 1) u G C0(A ): 2) u(x) >  1 д.тя x G C 3) u прииадлсжнт классу ACL. Также обозначим

n

(2.1)

| ∇ u|

При p > 1 величину capp E = capp (A, C)

= inf ueWa(E)

Z^{1w|p dm(x)}

A

(2.2)

называют p-e.MHoemmo коидсисатора. E.

В дальнейшем при p > 1 мы будем использовать равенство (см. [16, теорема 1])

capp E = Mp(A(dA, dC ; A \ C )).

(2.3)

Известно, что при 1

p capp E > nOnn

n-p p — 1

p-1         n-

[m(C )] ~

(2.4)

где On — объем единичного шара в Rn (см., например, [17, неравенство (8.9)]).

• 3.    О степенном порядке роста нижних Q-гомеоморфизмов

Вата- дал.... B r = ^{{x G Rn} : | x | < r ). Bn = ^{x ^{G R}" : | x | < ^1}. S, = ^{x ^{G Rn} : |x = r >. On — ооъем едшшниого шара, Bn в Rn 11 w_n-i — плошадь едзшинной сферы Sn ¹ в Rn.

Ниже приведена, лемма, об оценке искажения емкости сферического конденсатора, при нижних Q-гомсоморфнзмах.

Лемма ЗЛ. Пусть f : Bn ^ Bn, n > 2, — нижний Q-гомеоморфизм относительно p-модуля при p > n. Предполоялы. что для некоторых конечных чисел X > 1. а > Он C0 > 0 выполнено условие где

λε

, - [ _____dr_____

J kQk^-L. (r)

^        p— n+1

V E ^{G (0,} Eo ), Eo ^G

0X

(3.1)

IIQk n—1

p — n+1

(r)

f n — 1

Qp—n+1

S r

p — n+1

(x) dAn-Л ^n—1

Тогда имеет место оценка cap p p — n+1

-----          --ⁿ¹   a(n— 1)

(fBXe,fBA 6 Co p^—n+1 E p — n+1 .

(3.2)

C

A = A(0, £1, Е2) = {x Е Rn : Е1 < |x| < Е2},   0 < Е1 < Е2< 1.

Тогда ( B _£2 ,B ₅₁) - кольцевой конденсатор в Bn 11 ffB_e2 JB_S1 ) - кольцевой конденсатор в Bn.

Пусть Г* = A(fS51,fS£2,f A). Тогда согласно (2.3) имеем равенство capp—n- (fBE2,JB£i) = M n (Г*).(3.3)

По лемме 1.2 получаем, что е2

___          Г dr          ^{p —} n +1

• capж. (fBe2,fB=1) 6 ( J II Q| n—1 (r) )        •

X51        p —n+1/

Далее, выбирая в (3.4) Е1 = е < Е₀ < 1 i1 е₂ = Хе. получим

/ Ае             _х n- Д

____ Г dr          p—n+1

cap— В_— (/BA^/B) 6                          .             (З.б)

^{p — n+1}                                II Q I n —1 (r)

X5        p — n +1

Из условия (3.1) вытекает оценка (3.2). B

Следующий результат является аналогом известной леммы Икомы — Шварца об оценке нижнего предела, см. теорему 2 в [121-

Теорема 3.1. Пусть f : B n ^ B n, n >  2 , — нижний Q-гомеоморфизм относительно p-модуля при р > n, удовлетворяющий условию f (0) = 0. Если для некоторых конечных чисел X >  1, a >  0 и С_о >  0 выполнено условие

λε е" / или dr с 1 > Co(

HQH n —1 ^(r) 5

для любого Е Е (0, Ео). Е0 Е (0, А)• то liminf fx^ 6 vo C--p—n, x→0 |x|p-n0 0

где v₀ — положительная постоя!шая. зависящая только от n и р.

C Рассмотрим конленсатор ffB^jBg ) , е Е (0,е_о ). Е₀ Е ⁽ 0 , ¹). В силу леммы 3.1 имеем оценку -----             --ⁿ __¹__ cr(n—1)

cap      (fB_Ae,fB_e) 6 C ^p—n+1 е p—n+H .                    (3.8)

p — n +1

Используя соотношение (2.4), получаем

n(p — n+1) — p capp—n- (f BXe, fBe) > vi [m (fBe)] n(p—n+1) ,                  (3.9)

где v1 — константа, зависящая толью з от размерности пространства, n ii р.

Комбинируя (3.8) и (3.9), заключаем, что n" ^n

m(fB_e) 6 vo Co ^p—n е p^—n,                            (3.10)

ν0                                                    n p

Учитывая, что f (0) = 0. получаем и, следовательно,

n

6 m (fB_e)

(3.11)

n Im (^fBe) ^{min |f (x)|} 6 \ —5—-. | x |= e Un

Таким образом, учитывая неравенства. (3.10) и (3.12), имеем

(3.12)

lim inf

I f (x) l

σ

σ xMO  |x| p-n

m=n |f (x)|

= lim inf —— Д- -- 6 lim inf л >o       £ p-n           e >o

m fB ε

σn

U n E p ^-n

n

p - n

6 vo C_o    ,

где vo — положительная постоя:шая. зависятпдя только от n п р. B

Следствие 3.1. В частности, если для некоторых конечных чисел X >  1 выполнено условие

И

Co > 0

λε p-n

^ε k Q k

ε для любого e E (0, £o), eo € (0, у) , го

dr

n — 1 p — n +1

ТУ >  Co

(r)

(3.13)

If (x) I lim inf —:—:— x ^o | x |

p - n

6 vo C_o    ,

(3.14)

где vo — положительная постоятшая. зависящая только от n п р.

Теорема 3.2. Пусть f : B n ^ B n, n >  2, — нижний Q-гомеоморфизм относительно p-модуля при р > n, удовлетворяющий условию f (0) = 0. Если для некоторых чисел q_o E (0, то ), y E [0, р — n) выполнено условие

Wn —1Г^{П— 1}

Г     n — 1

Q^p—n+1 (x) dAn—1

S r

p — n +1 n — 1

6 qo r

-

γ

,

(3.15)

лля П.В. r E (O,ro). ro E (0, e ), to

|f(x)|            p lim inf —— - 6 vo qo x^0 |xp p-n

-

n

,

(3.16)

где vo — положительная константа, зависящая только от и р.

n

C Из условия (3.15) вытекает оттенка.

kQk n—1

p — n +1

(r) =     Q

S

r

Пусть X = e ii a = p — n

-

ε p - n - γ

где Co = — ω _n

_e n + Y — p _— 1

— n + n — 1

— 1

n — 1

p ^-n+1 (x) dA_n—1

)

p — n +1 n — 1

6 ω

p — n +1

’n— ^—1 qo r^p—n—Y+1

Y- Из неравенства (3.17) следует условие

eε k Qk ε

dr

— ^(r) p - n +1

>

εp-n-γ p — n+1 , . n—1 Wn—1  qo

eε / ε

dr

r P - n - Y +1

= Co ,

.

(3.17)

(3.18)

q o ( n + Y - p )

Применяя теорему 3.1 с параметрами А = e. a = p — n — y и C_o = _{p —} n ++ ^Y p ^—1--- ^n—n—¹ qo(n+Y-p)

получаем оценку

lf(x)l            p liminf —---y- 6 voq x^0 |x|1—p-n       o

-

n

,

(3.19)

где vo — положительная hoctohi шая. зависящая только от n ii p. B

Следствие 3.2. В частности, если для некоторого конечного числа qo > 0 выполнено условие

Wn-yrn-1

f     n — 1

Q^p—n+1 (x) dA n - 1

S r

p — n + n — 1

6 q o

(3.20)

для п.в. r E (0, ro). ro E (0, e). to lf(x)l . p W IT 6 voqo

-

n

,

(3.21)

где vo — положительная константа, зависящая только

n

p

Следствие 3.3. Если Q(x) 6 K <  то для п.в. x E Bn, то

I f (x) l lim inf —:—:— x T) | x |

6 v o K p^—n ,

(3.22)

где v o — положительная константа, зависяшая только от размерности пространства n

p

Лемма 3.2. Пусть Q E L_a(Bⁿ), a >  pnn , p > n. Тогда при А > 1 имеет место оценка

λε

^εσ     k Q k

ε

dr

^(r) p — n +1

> -co

^> k Q k α

(3.23)

™ „,,«,„ ^{e e} (0, 1 ). г_T. k Q k a = (R Bn ^Qa (x) ^dm(^x)) X Л = ^p - nnn ная постоянная, зависящая только от n, p, А и a.

C Пусть А > 1. Заметим, что

II Co — положитсль-

λε

/ n — 1

k Q k n—1 (r)

p — n +1

ε

dr n—1

.

(3.24)

k Q k n

p — n +1

1 ^(r)

Применяя теорему Фубини и неравенство Гёльдера с показателями

q = — q p—n+1

q0

= p n—1 *

имеем

λε k Qk ε

dr

n — 1 ^(r) p — n +1

)

n — 1 p — n +1

__ p /      n — 1

((А — 1)e) p - n +1    Q p - n +1 (x) dm(x),

(3.25)

A

где A = A(0, e, Ae).

Применяя еще раз неравенство Гёльдера с показателями q = ^p^-—+¹) a(p— n +1)

a(p — n+1) — П+1 ' получаем

>

II q

λε k Qk ε

dr

n — 1 p — n +1

A

n — 1 p — n +1

6 c1 E⁶

j Qa (x) dm^j

A

n — 1

a ( p — n +1)

,

(3.26)

где 9 =

α

( n —1)( ap — an — n ) a ( p — n +1)

ii c i — положительная постоя!шая. зависящая только от n. p. А

Отсюда вытекает оценка

λε

Г dr           со

(3.27)

J k Q k Ж-1 (r) > k Q k a

5         p— n+1

где kQka = (JBn Qa(x) dm(x))   a = a(p ^ n 11 co — положительная постоянная, зави сящая только от n. p. Ana. B

Теорема 3.3. Пусть f : Bn ^ Bn, n > 2, — нижний Q-гомеоморфизм относительно p-модуля при p > n. удовлетворяющий условии) f (0) = 0. Ес мп Q Е La (Bn), a > p-nn. to liminf Ц—Н- 6 vokQka-n,                    (3.28)

x ^⁰   | x | a(p —n)

где k Q k_a = (J Bn Q^a(x) dm(x)) ^a — норма в прострапстве L_a(Bⁿ) i1 v ₀ — положительная постоянная, зависящая только от n, p и a.

C Пус-ть А = 2. Поскольку Q Е La (Bn) 11 a > p^. то из леммы 3.2 следует, что функция Q удовлетворяет условию (3.6) с параметрами a = ^p-n-n. Co = -c— Применяя теорему 3.1. получаем опенку                                           a liminf   1f(x)n    6 vokQka-n,                           (3.29)

x ^⁰   | x | a(p — n)

где ||Q k_a = ^(JBn Q ^a( x ) dm ( x ))¹ - норма, в прострапстве L _a(Bⁿ) 11 v ₀ - положительная постоянная, зависящая только от n, p и a. B

• 4.    Приложения к классам Орлича — Соболева

Напомним некоторые определения. Пусть D — область в Rn, n > 2. Гомеоморфизм f : D ^ Rn называется отпобраснсением с конечным искаснсением, если f Е W^c1 и kf 0(x)kn 6 K(x) • J(x,f)                                 (4.1)

для некоторой п.в. копенной <1>упкппп K (x) >  1, где f 0(x) - якобиева матрица f, k f⁰(x)k — ее операторная норма: kf 0(x) k = sup| h | ₌₁ | f0(x) • h | 11 J(x,f ) = det f 0(x ) — якобиан отображения f.

Впервые понятие отображения с конечным искажением введено в случае плоскости для f Е WOc² в работе [18] (см. также [19]).

Следуя Орличу, для заданной выпуклой возрастающей функции у : [0, то ) ^ [0, то ), ^ (0) = 0. обозначим символом L^ пространство веек (]>ункцпй f : D ^ R таких, что

[ у flflxHA dm(x) < то                           (4.2)

λ

D при некотором А > 0 (см., папример. [20]). Здесь m — мера. .Лебега в Rn. Пространство L^ называется пространством Орлича.

Классом Орлана - Соболева W^(D) называется класс всех локально интегрируемых функций f, заданных в D, с первыми обобщенными производными по Соболеву, градиент Vf которых принадлежит классу Орлина локально в области D. Если же. более того. Vf принадлежит классу Орлпча в области D, мы пишем f Е W ^( D). Заме тим, что по определению W^ С W^¹. Как обычно, мы пишем f Е W^, если p(t) = tp, p >  1. Известно, что непрерывная функция f принадлежит классу W^ тогда п толь ко тогда, когда f Е ACLp, т. е. если f локально абсолютно непрерывна на почти всех прямых, параллельных координатным осям, а первые частные производные f локально интегрируемы в степени p в области D (см. [21. разд. 1.1.3]).

Далее, если f — локально интегрируемая вектор-функция n вещественных переменных xi,..., xn, f = (fi,..., fm), fi Е W^c¹, i = 1,... ,m, ii

У P (|Vf (x)|) dm(x) <  to,                               (4.3)

D где |Vf (x)| = УPm=1 Pn=1 (f У’ T° MLI С110ва пишем f Е W^. Мы также используем обозначение W^ в случае более общих функций р, чем в классах Орлича, всегда предполагающих выпуклость фуиктщп р п ее нормировку р(0) = 0.

Пусть p > n - 1, а = p—n+y. Ранее (см., например, [8-10]) в теоремах о локальном поведении классов Соболева и Орлича — Соболева мы пользовались p-внешней дилата-

цией
		( kf0 (x)kp |J (x,f )| ’	J(x,f ) = 0;
	K o,p ( x, f ) =	1,	f 0 ( x) = °;	(4M)
		_TO,	.

В дальнейшем мы будем пользоваться а-внутренней дилатацией

( |J(x,f)l la(f0(x)) , |J(x,f )| = 0; Kl,a(x,f) = < 1, f 0(x) = 0; (4.5) .TO, , га lf0(x)) = штц^ |f0(x) • h\.

Известно, что

Ki,n(x,f ) 6 KOn4x,f )                            (4.6)

(см., например, [22, разд. 1.2.1]).

Из соотношения (4.6) легко следует неравенство

Ki,a(x,f ) 6 KO^-p¹ ( x,f ) .                           ММ

Действительно, су                                        а(п — 1)

^а              а                                а

Ki,a(x,f ) = K nj xf ) |J^1-n ( x,f ) | 6 Kon (x,f ) |J^1-n ( x,f ) | = KO^-p¹ ( x,f ) .     M.S)

Известно, что Ki,2 = Ko,2 ^ПРи n = 2, но при n >  3 в (4.6) может иметь место строгое неравенство, как это показывает элементарный пример сжатия вдоль одной из осей.

Следующее утверждение см. в [11, теорема 1].

Предложение 4.1. Пусть D и D' - области в Rn, n >  3, p >  n — 1 ид : (0, то ) ^ (0, то ) — неубывающая функция такая, что для некоторого t* Е (0, то )

∞

Г t    n-2

J v(t).

dt <  ∞ .

(4.9)

t ∗

Тогда любой гомеоморфизм f : D

→ D ⁰

ппжппм Q-гомеоморфпзмом относительно п-модуля с Q = Kа—1 ■ I,α

конечного искажения класса W lO^ является

а = —Р—т а   p-n+1

Следствие 4.1. Любой гомеоморфизм с конечным искажением в Rn, n >  3, класса i

W^q ^п!^зи q > n — 1 является нижним Kj-¹ -гомеоморфизмем относительно p-модуля при p > n — 1. a = —p-pr.

p             p-n +1

Следующий ряд теорем вытекает из предложения 4.1 и теорем пункта. 3.

Теорема 4.1. Пусть f : Bn ^ Bn, n >  3 гомеоморфизм с конечным искажением класса W lO^, щ щ у : (0, то ) ^ (0, то) — неубывающая функция, удовлетворяющая условию (4.9) 11 f (0) = 0. Прсдпол<. )жш. что p > n н для некоторых конечных чисел X >  1. a > 0 1 1 C_o > 0 выполнено условие

λε ет f Л > Co                             (4.10)

/ ча (r)

для любого е Е (0, £0)• Eo Е (0,1). где kI,a(r) = у

Ki,a(x, f ) dAn-1 a = - n _{+ 1} .                  (4.11)

S r

Тогда имеет место оценка.

lim inf fx ¹ 6 vo C_n- p - n ,                         (4.12)

^{x → 0} | x | ^{p-n 0 0}

где v o — положительная константа, зависящая только от размерности пространства. n. p. X п a.

Следствие 4.2. В частности, если для некоторых конечных чисел X >  1 и C0 > 0 выполнено условие

λε

Ep— f * > Co                       _(4ЛЗ)

/ ki“« 1 ^(r)

для любого е Е (0, Eo). E0 Е (0,1). где ki,a(r) = /‘Ki,a(x,f) dA, a =----p——,                  (4.14)

p — n + 1

Sr то при p > n имеем lim inf |f4_21 6 voCn p-n,                              (4.15 )

x→ 0     | x |            ⁰

где v_o — подожитечвиая константа, зависяща.я толвко от размерности пространства, n. p п X.

ПРИМЕР. Предположим, что n >  3 и p > n, ст > 0. Пусть f : Bn ^ Bn, где

f(x) = я|х| p—n при x = 8, f(0) —0.

Касательная и радиальная дилатации f на сфере Sr — {x Е Rn : |x| = r}, r E (0,1), легко вычисляются:

|f(x)|     _

»T=— = H p—n

и

δ r

σ

p -

| x | n

т — p + n

p - n

.

Заметим, что 6T > 6r. Следовательно, ввиду сферической симметрии мы видим, что

^n-1 ^r

KI,a^(x,f ) =   _{5 a}

n — 1

p   n p — n +1     (n— 1)( т — p + n )

|x|     p ^—n+1

p

σ

,

a —------ p — n + 1

.

Sr

p kI,a(r) — I KI,a(x, f) dAn-1 — ^n-1 (

S r

n — 1

— n p—n+1

σ

(n—1)(т+1)

Г p — n +1

.

Откуда вытекает равенство

λε

^E’ )■ ε k

dr

σε ^σ

n — 1

■ I— (r)

ω p - n

p — n +1 n—1

λε у r-C+P dr = ш ε

n — 1

p — n +1 n-1

1—

-σ

---= Co > 0.

p - n

Этим показано, что условие (4.10) нашей теоремы выполнено. С другой стороны, легко видеть, что lim x >0

If (x)|      ,

T         ¹ .

| x | ^p-n

(4.16)

Замечание 4.1. Построенный пример показывает, что найденный порядок роста в оценке (4.12) является точным.

Теорема 4.2. Пусть f : Bn ^ Bn,n > 3, — гомеоморфизм с конечным искажением класса W^, г; je ^ : (0, то) ^ (0, то) — неубывающая функция, удовлетворяющая условию (4.9). p >  n п f (0) — 0.

• 1)    Если для пекотор!JX конечных чисел 6 Е |^0, ^{(p -} nn(+ ^{- 1)} ^ и к₀ > 0 выполнено условие

  Шп-1Г^п-1

  
  

  I Kl,a(x,f )

  S r

  
  

  dA_n-1 6 Kor ⁶

  
  

  (4.17)

  
  

лля я. в. r Е (0, ro)• ro Е (0, e 1). то lim inf x >0

If (x)|

1 - e ⁽ p ^— n +1) |x|    ^(n—1)( p ^—n)

p — n +1

/      (p—n)(n—1)

6 v0 Ko         ,

(4.18)

тле v o — положительная константа, завнсяшая только от размерности пространства n

p

• 2)    Ес ли Ka—¹ (x,f ) е Le ( Bn), в >  p-n то

  lim inf x→0

  
  

  I f (x) l | x | ^{1 -} e c p - n

  
  

  1        1

  6 v oi K a nr

  
  

  (4.19)

  
  

• ¹                  в,-            А в

где ||K/“_a ||e = I J®™ Kj- (x,f )dm(x) I — норма в пространстве Le ( Bn ) и vo — положительная постоянная, зависящая только от n, p и р.

Следствие 4.3. Если для некоторого конечного числа к₀ > 0 выполнено условие

n

"—Д^ iKfa^ (X,f) ^dAn-1 6 К О ω n-1 r

(4.20)

(4.21)

Sr для п.в. r е (0, ro). r0 е (0, e-1). то

If(x)I .     (p-nn+iD lim inf —:—:— 6 VoK         , x→0     |x|           0

где vo — положительная константа, зависянь hi только от размерности пространства n п p.

Следствие 4.4. В частности, все результаты имеют место для гомеоморфизмов с конечным искажением класса Соболева W lOcq щ ж q > n - 1.