О связи преобразования типа свертки и наилучшего приближения периодических функций

DOI:

Пусть X{ж} — произвольное линейное нормированное пространство, в котором норма элементов ж G X обозначается через ||ж||х и система элементов {жп} (п = = 0,1, 2,...) — заданная система линейных независимых элементов в этом пространстве. Тогда для каждого элемента ж G X существует полином ^”=0 с$0)жу, для которого выполняется равенство п                       п

|| ж - »⁽⁰ ._{X v} = inf 1| ж - ^с_уж_у | х = Е п (ж^ х .

v=0             ^{C v}        v=0

Величина Е _п (ж) _х называется наилучшим приближением элемента ж G X порядка п полиномами ^2П=₀ с^ж ^ в метрике пространства X относительно системы элементов { ж _п } (п = 0,1, 2,...).

Под пространством L _p понимают совокупность 2п-периодических функций /(ж) G G L _p , для которых | /(ж) | ^р интегрируема по Лебегу с нормой

НУIk = Q 1/1 (ж)|р^ж)    (1 < р< ^), а при р = то

Н У IIl^ = ^таг sup ^{1 / (ж) |} . ж £ [0 , 2п]

Для пространств L _p (1 <  р < то ) рассмотрим преобразования типа

^{F (/}; у;^ж;

h) =     / (ж — uh)dy(u),

-∞

где /(ж) G Lp; h — произвольный параметр; у (ж) — произвольная функция ограниченной вариации на (-то, то) тождественно не равна нулю и удовлетворяет условиям f dy(u) = 0, V(у) = [ |dy(u)| < то. -∞               -∞

Интегралы типа (1) представляют собой обобщение некоторых преобразований, связанных с различными изучаемыми обычно характеристиками функции /(ж).

Для преобразований (1) в работах [4] и [5] рассмотрена общая задача о возможных зависимостях

G ^{( /} ; у;^h; р) = || /    ^{/ (ж}

-∞

- ^uh)dy^{(u) |} _{L p}

для двух различных величин у 1 (ж) и у ₂ (ж).

В частности, в работе [5] установлено, что если /(ж) G L _p (1 <  р < то ), а у 1 (ж), у ₂ (ж) две конечномерные на ( —то , то ) функции, для которых при / > 0 выполнено условие у ₂ (ж) = ж¹Е (ж), где F (ж) — преобразование Фурье некоторой меры р(ж), то имеет место неравенство

W(у2; /; h)L, < М(yi,y2, р) ^^1 WY(yi; /; t)t,   + hY “ WY(yi; /; Bt)L„^Y^ I Y , где

^ (у; /; h^L p = sup ||^{G( /}; у; ^h; p) ^ _{L p} , \t\

Y = min(2, p) при 1 <  p <  то и y = 1, если p = то , а M(у 1 ,у ₂ , p) и В — некоторые константы.

В 1970–1971 гг., продолжая и уточняя результаты работ [4] и [5], М.Ф.Тиман [3] получил точные по порядку оценки как сверху так и снизу для величины (2) в зависимости от наилучших приближений функции /(x) G L _p (1 <  p < то ) и доказал следующее утверждение, которое будет полезным при установлении результатов данной статьи.

Теорема. [3] Пусть nv+1-1

| y(^ _v h) | , y (x) = / exp(-iux)dy(u).

-∞

5(n v , h)

= £ | У (рА) - У ((ц +1)h) | +

H= n v

Тогда для каждой функции / (x) G L _p (1 < p <  то ), при любом h (0 < h <  1), имеет место неравенство

^{G ( /} ; у; ^h; p) <  C(y^,p ⁾

{ m

∑︁ v=0

E ^ - 1 (/X5 ^Y (n v h)+E ^ _{m +}i - i (/) L p

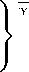
где y = min(2,p), n0 = 1 < n1 < n2 < ... < nk < ...; '    > q > 1 (k = 1,2,...), kk nm+1 < j; C(y,p) — константа, которая зависит только от у и p.

• 1.    Основные результаты

В этой статье мы приводим некоторые утверждения, которые дополняют, а в ряде случаев и уточняют результаты работ [3–5]. В порядке обобщения некоторых из результатов рассмотрим здесь вопрос о зависимости между величиной (1) и наилучшими приближениями E _B (/) _{L p} , учитывая особенности случая, когда 1 <  p < то .

Теорема 1. Пусть 2п -периодическая функция / (x) G L _p (1 <  p < то ) . Если E _B (/) _{L p} — величина наилучшего приближения функции / (ж) тригонометрическими полиномами порядка не выше n в метрике L _p (1 <  p < то ) , то справедлива оценка

G(/ ; у; h; p) = ЦЕ _у (/; x; h) | L p <  2E o (/) L p p(1,h) +

m

+ 2 £ E , k (/) L p p(n _t ,h) + V (у)Е „ _+1 (/) L p , k=0

где

B y (/;x; h) = / /(x - th)dy(t),

-∞

h =

ⁿ m +1

n o = 1 < П 1 < П 2 < ... < n ^ < n ^+1 < ...,

p(n _k , h) = УП      £ y (ph) cos pt

dt,

^{V (} у)=[   ^{| d}У^{(t) | ,}

-∞

∞

y (x) = /     exp(—i^t')dy(t'),    /    dy(t)

= ⁰,    y ^{(- t )} = y ^{( t )} .

-∞              -∞

Теорема 2. Если функция /(х) G L _p (1 < р <  то ) имеет ряд Фурье

∞

° с .

+

П =1

а _п cos пх + b _n sin пх

с монотонно убывающими коэффициентами { а „ , b „ } , то имеет место соотношение

G^{p ( /} ; у; ^к ; р) <  М (y^)

{ т                                  Л

Е Щ . -1У ) l , 8 (2 ^V , h) + E^-W ) l , |,

где

2 ^{v +1} -1                                                          .

6(2 ^v ,h) = Е №) - У ((и + 1)h) | + | y (2 ^v h) | (h = —^ m ।

H=2 ^V

У (х) = [ exр(-ixt')dy(t), / dy(t) = 0, y (-t) = y (t).

-∞              -∞

В некотором отношении обратным к теореме 2 является следующее утверждение.

Теорема 3. Пусть коэффициенты Фурье 2п -периодической функции / (х) G L _p (1 <  < р <  то ) монотонно убывают и при h = 2 ^{-( m +1)} функция y (t) удовлетворяет условиям

^Н (^ v ; К) = |

\yWV ^p E Z=0 № h) | ^p , 2 ^V-1 <  h <  2 ^V - 1, (v = 1, 2,...,m + 1), 0,                           H > 2 ^{m +1} ;

2 ^{v +1} - 1

Н ( h ; v ; h) <  С, Е | H ( h ; v ; h) - Н ( h + 1; v; h) | <  C (v = 1, 2,...,m + 1).

H=2 ^V

Тогда справедлива оценка

m

k=0

где константа C 1 (y,p) не зависит от h и функции / (х) .

Заметим, что теорема 1 для случая пространства L _p (р = то ) приведена в работе [3]. Теоремы 2 и 3 уточняют оценку (3), содержащуюся в [3], и оценку

т

Е 1 У (2 " К)Г^ 5 ^ - 1 (/ ) l „ <  C 1 (y,p) { G ^Y (/; y; h; р) + E^,^/ )_L, } ,        (7)

k=0

где у = тах(2,р). Оценка (7) также приведена в работе [3] для функций с произвольными коэффициентами Фурье.

Указанные уточнения касаются возможности замены показателя в оценках (3) и

• (7)    на у = р для случая функций с монотонными коэффициентами Фурье.

• 2.    Доказательства основных результатов

Доказательство теоремы 1. Рассмотрим последовательность тригонометрических полиномов {Т _{П к} (ж) } , которые осуществляют наилучшие приближения порядка не выше п функции /(ж) в метрике пространства L _p . Тогда, так как

m

Т „ _{т +}, =т „„ + £ Т . - т „ ₍ } , к =0

то

m

F , (Т „ т+1 ; ж; А) = F , (Т , ; ж; А) + £ F , Т     - Т„„ ; ж; А } .

к=0

Отсюда, благодаря неравенству Минковского, находим, что m

« F , (Т_ +1 ; ж; А) Н ь » < « F , (Т , ; ж; А) H r , + £ « F , { T,„ ₊i - Т„„ ; ж; А }|| ь , , к=0

а для величины С(Т _{П т+1} ; у; А; р) получим неравенство

m

^{G ( T} n m+i ;у;^А; р) <  ^{G ( T} , ;у; ^А;р) + £ ^{G { T} r ^₁₊i - ^Т п _к ; у; ^А; р ^} .            (8)

к=0

Докажем, что для каждого полинома Т _п (ж) выполняется следующее неравенство

G(T _n ; у; А; р) <« Т _п (ж) « ь _р

П£ (* 2п ^п

•А /2/   Уу(^АА)ео8 kt

^{N п у}0   к =1

dt = Н Т ^ (ж) Н _{£ р} р(п, А).

Действительно, пусть

п

Т _п (ж) = У С к ежр(гкж), к=-п

тогда

^С к

1       ^2п

^— J  T_п(t)ежр(—гkt)dt,

п

п                             п           1 Г

F , (Т П ;ж; А) = £ У (кА)с к ежр(-гкж) = £ У (кА) — к„                      ^2п V0

2п

T _п (t)ежр(—гkt)dtежр(гkж),

или

F , (Т п ; ж; А) =

V2n

р 2п

Т п (ж + t) ^£ У (kА)ежр(ikt)dt. к=-п

Отсюда, применяя обобщенное неравенство Минковского, получим искомое соотношение (9).

В силу оценок (8) и (9) будем иметь

m

^{G ( T} п m₊1 ; у;^А; р) <  ^G(T , ; у;^А; р ^{) +} £ II^ n fc+i    ^Т п _к « ь , Р^(п к ^,А).

к =0

Так как      dy(t) = 0, то

G(T i ; y; h;p) = G(T i - T o ; y; h; p).

Пусть для тригонометрических полиномов {Tnk(ж)}, которые осуществляют наилучшие приближения порядка < п функции /(ж) Е Lp (1 < p < то), имеем ||/ — - ТДЬр = Еп(/)Lp. Тогда llTnk+i - Т»к IlLp < ||Tnk+i - У IlLp + ЦУ - Тпк IlLp < 2Enk (/) Lp.

Следовательно, благодаря этой оценке получим

m

G(T _{n m}+i ; y; h; p) <  G(T - T o ; y; h; p) + £ H^ - T | _L p p(n _k , h) <  k=0 m

< 2Eo(/)Lpp(1, h) + 2 £ Enk(/)Lpp(nk, h).(10)

k=0

В силу неравенства Минковского имеем

G(/; y; h; p) < G(/   Tnm+1; y; h;p) + G(Tnm+i; y; h; p).

Кроме того,

G(/ Tnm+i; y; h;p) < V(y)Enm+i(/)Lp.(12)

Из оценок (11), (10) и (12) вытекает неравенство (4). Теорема 1 доказана.

Доказательство теоремы 2. Не нарушая общности, можно доказать оценку (5), считая, что рассматриваемая функция /(ж) является четной и имеет ряд Фурье вида

∞

°о .

— +    a _n cos пж.

n=1

Тогда

∞

^{G ( /} ; y;^h; p) =   /  ^{/ ( ж} - ^ht)^dy ⁽ t)

-∞

∞

^L p

∞

y (hv)a _v cos vж    ,        (13)

^V =1                   L p

где функция У (ж) была определена в формулировке теоремы.

После применения неравенства Минковского в (13), будем иметь

	2 m +i - i		∞ ⃦
G(/; y;h; p) <	y (hv)a v cos vж	+	У2 y7(hv)a v cos vж	= S 1 + S 2 .	(14)
	ν=1	L p	v =2 m +i	L p

Заметим, что при p <  2 неравенство (5) превращается в неравенство (3).

Для p >  2, в силу известного неравенства Пэли (см. [1, с. 182]), которое имеет вид

i

{ ^            p

Е |Сп|РПр-2   , находим, что sp =

∞

У y (hv)a _p cos vx v=2 ^{m +1}

P

≤

^L p

∞∞

Bp Е  ly(HlPaVvP-2

где V(у) = /У ^у^.

Кроме того, А. Конюшковым (см. [2, с. 63]) установлено, что

∞

Е a^- pE^p_2m+1 (f )Lp.

v=2^m+1

Следовательно, в силу этого неравенства, получим

S^p2 _PV(y)E^p_2m+1(f)Lp.

Теперь для первого слагаемого в правой части (14), при р> 2, применяем неравенство Пэли и получим

S^p=

2^m+1-1

У y(hp)av cos vx v=1

p

Lp

2^m+1-1

<Bp Е |y(Av)|^Pa^pv^P-2

v=1

m 2^v+1-1

= BpЕ Е |?(h^)|^pa^pv^p-2

p=0 ^=2^V

.

Обозначая для краткости

2^v+1-1

Ак = Е akk^WhW, Гк k=2v

∞

= Е a^^P-2

р=к

,

в к = 1У(кК)1^Р,

мы можем написать

2^v+1-1

У Гк (вк - вк-1) + r2v+1 P2V+1-1. k=2^v+1

Подставляя вместо г_ки в к их выражения в последнем тождестве, получаем

∞

2^v+1-1 го

Ак = lyp^l- Е ap.к--2 + Е   E°P.HP-2  (1УИ)1" - У((н - 1)Л)1") - k=2v

k=2^v+1  р=к

- f is -■.-■; i»((2^v+1- i)A)i^p.

Так как коэффициенты Фурье функции f (x) монотонно убывают, то с помощью неравенства А. Конюшкова (см. [2, с. 63]), имеем

∞

Гк = Е aP.^^P-2< CpEP(f )Lp.

==k

Поэтому

^к< ВрСр  |№(2^vh)|^РЕ»v

2^v+1-1

1(/)1, + Е Ер-1(/)ж,№Л)|" -|$((* - 1)Л)|^р k=2^v+ 1

.

Отсюда следует, что т зр < С(8,р) Е l№(2vЛ)lРЕР.

v=0

т 2^v+1-1

1(/)1, + Е Е Ек^р-1(/)ж,|№(*Л)1^р-|?((t - 1)Л)1^р v=0k=2^v+1

.

(16) Подставляя соотношения (15) и (16) в (14), получаем оценку (5), что и заканчивает доказательство теоремы 2.

Доказательство теоремы 3. Рассмотрим величину

Um(/; № h) = tf^,-1(/)г, 1№(2^кЛ)|^рГ (1 <Р< 2). к=0

Из теоремы М. Рисса (см., например, [2, с. 55]) следует, что при 1 < р < то

п

II/(ж) - Е^Лж(ж)1к <СрЕп(/V,, ц=0

где Л_ц(ж) — коэффициенты Фурье функции /(ж) G L_p; С_р лишь от р.

Воспользовавшись этим соотношением, будем иметь

—

константа, зависящая

т

∞

т

∞

ит(/;№; л)< С„Е1№(2^кh)n Е ^л«(ж) НЕ,  ¹Е   ^;'Ч1^рИЕ^^Ж,, (17)

к=0

^=2^к

к=0

v=k

где

2^v+1-1

△v^(/;^ж) = Е ^л^^(ж).

^=2^v

Применяя неравенство Литтльвуда — Пэли (см. [1, с. 315]) ко второй сумме в правой части (17), получим

∞

Е М/;ж)

v=k

^р           л2п / ^го                \ 2

<Ср/_о  ^Е1^д’(/;ж)1²«^ ^ж.

Тогда при (1 < р < 2) соотношение (17) принимает вид

„ 2п т              го ит(/; № Л) <     Е 1№(2кА)1Р Е lAv(/; ж)|рйж =

^{J 0} к=0          v=k

Г 2п т          т                 гП т           га

=    £|№‘ 1< £| Д,(/; xffdx +    £|у(2» 1< £ kv(f; _iE)|”dx = I, + 12.

⁰к=0          ^=к                  ⁰к=0          v=m+1

Оценим I1. С этой целью переставляя порядок суммирования, находим, что

£2п т           т                    „2п т              к

I1 =    El »(2^{к A})I'EJ Mf; x) V dx = ^ El Дк(/; x) |^pE |у(2«Л) pdx.

Применяя известную теорему Марцинкевича о мультипликаторах в периодическом случае (см. [1, с. 168]), с учетом условий теоремы для величины p(t), получим

2п 2™+!-1

Ii < С_р V WhU(a)\^pdx.

⁰Ц=1

Благодаря тому, что частичные суммы рядов Фурье в пространствах L_p (1 < р< то) за порядком не больше нормы функции, находим, что

I1 < Cp\\F_p(f; x; h<p = СрG^p(f; p; h; р).

Теперь оценим второе слагаемое I₂.

г 2п т             га                                   т

I2 =     £ l^2‘h)l" £   ^х-(f; x)l^pdx < sp„+₁_i(f)Lp £ l?(2‘h)|^p<

⁰к=0          у=т+1                                к=0

< 5p_m+!—i(f)Lply(mh)\^p< V(^^pE2_m+₁-i(f)Lp.

Таким образом, благодаря оценкам величин I1, I₂, из соотношения (18) следует утверждение теоремы.

Выводы

Заметим, что в случае, когда р > 2, для любой системы чисел с. известно неравенство

{га          p        га

£k„\p   <  £k„\2

n=1n=1

а для 1 < р < 2

{га          2        га

£ I с. |2    < £ | cn |p

П=1

Из этих замечаний вытекает, что оценка (5) по порядку лучше, чем оценки (3), а оценка (6) за порядком лучше, чем

т

£ IЙ2‘h)IYS2*-1(/)Lp < С(y,p){G''(f; p; h;р) + S2„+1-i(f)Lp}, к=0

которая приведена в работе [3], где y = max(2,p).