О свойствах показателя Ляпунова на проекторе класса Бэра

В работе [1] центральное место занимает вопрос о принадлежности или непринадлежности конкретных ляпуновских показателей тому или иному классу Бэра, доказана непринадлежность минимальных полунепрерывных сверху мажорант показателей Ляпунова первому классу Бэра». Отсюда возникает актуальность исследования следующего вопроса: если существует проектор первого класса Бэра, то каковы свойства показателей Ляпунова? Для этого исследуется понятие проекции (в случае не- линейного отображения соответствующее отображение называется ретракцией) и построение равномерно непрерывной ретракции на выпуклое множество, а также проведен анализ различных свойств пространства X м .

Равномерно-непрерывные ретракты

Пелчинский [2] доказал, что пространство C [0,1] не дополняемо в пространстве D [0,1], то есть не существует проектора из пространства D [0,1] на его подпространство C [0,1], где D [0,1] - пространство всех ограниченных функций на [0,1], непрерывных в каждой недвоичнорациональной точке, непрерывных слева и справа в каждой точке и имеющих для каждого £ >  0 только конечное число «скачков», больших, чем £ . Но актуален следующий вопрос: существует ли между данными пространствами проектор первого класса Бэра?

Бэр Рене-Луи в 1899 году предложил свою классификацию разрывных функций:

• -    нулевым классом Бэра, называется множество всех непрерывных функций;

• -    если функция представляется, как поточечный предел последовательности функций нулевого класса, то она принадлежит первому классу Бэра;

• -    если функция представляется, как поточечный предел последовательности функций первого класса, то она принадлежит второму классу Бэра;

и т. д.

Введем алогичную классификацию для операторов:

• -    множество всех непрерывных операторов назовём множеством нулевого класса;

• -    если оператор P не входит в нулевой класс, но представим в виде: P ( x ) = lim P n ( x ), для V x , где каждый оператор P n непрерывен, то n ^М

оператор P называется оператором первого класса Бэра;

• -    если оператор P , не входит ни в нулевой, ни в первый классы, но представим в виде:     P ( x ) = lim P n ( x ),   где каждый оператор

n ^М

P n непрерывный, то оператор P называется оператором второго класса Бэра;

и.т.д по трансфинитной индукции.

Теорема 1. Не существует линейного проектора первого класса Бэра пространства D [0,1] на его подпространство C [0,1].

Доказательство. Для доказательства используем классическую теорему о принципе равномерной сходимости [3] из общего курса функционального анализа:

Пусть пространство E банахово, а пространство F нормированное и задано некоторое множество отображений {T a } _ае A с L ( E , F ). Тогда равносильны следующие условия:

• (1)    {T _a } равномерно ограниченно, т.е. || T _a ||< M для V a е A .

• (2)    {T _a } поточечно ограниченно, т.е. {T _a ( x )} _{а е} A ограниченно в пространстве F ^ || T _a x || ^ M x для Va е A .

Предположим, что проектор P ( f ) представим в виде предела непрерывных операторов, где каждый P m линейный:

P ( f ) = lim P m ( f ).

m →∞

Это означает, что P есть проектор первого класса Бэра. Если данный предел существует для каждого f , то по принципу равномерной ограниченности, это будет означать, что и

IIP(f )И = mm ।Pm (f )И ^ suP ।Pm (f )И < +” , то есть sup||Pm|| < +да, а этого не может быть. Таким образом, мы m приходим к выводу, что проектора первого класса Бэра между данными пространствами не существует. Теорема доказана.

Пусть X топологическое подпространство пространства Y .

Определение 1. [4] Непрерывное отображение r : Y ^ X называется ретракцией , если r ( x ) = x для любой точки x е X .

Определение 2. [4] Если существует ретракция r : Y ^ X , то X называют ретрактом пространства Y .

Определение 3. [4] Топологическое пространство X называется абсолютным ретрактом , если оно является ретрактом всякого топологического пространства, содержащего X в качестве замкнутого подпространства.

Рассмотрим случай существования равномерно-непрерывных ретрактов в пространстве C p ( X ).

Лемма 1. Для любого пространства X , если C p ( X ) содержит всюду плотное подмножество типа G _g из пространства R X , то пространство X является дискретным.

Доказательство. Предположим, что пространство X недискретно. Тогда функция g е RX \ Cp (X). Определим отображение F: RX ^ RX, такое что F(f) = f + g. Тогда отображение F есть гомеоморфизм RX на самого себя, и F(Cp (X)) с RX \ Cp (X). Таким образом RX \ Cp (X) также содержит плотное Gg подмножество из пространства RX, чего быть не может, так как пространство RX является бэровским, и в бэровском пространстве каждая пара плотных Gs множеств имеют непустое пересечение.

Теорема 2. Пусть X - вполне регулярное пространство и пусть дана равномерно непрерывная функция ф : X ^ R такая, что ф (x ) >  0 для любого x е X . Тогда выпуклое множество

L = {f е Cp(X):|f (x)|< ф(x)} является равномерным ретрактом пространства Cp (X).

Доказательство. Множество L является выпуклым, то есть

ft X + f;(1 - X) е L «| f} X + f2(1 - Л)| < ф,

рис. 1

для любого x е X выполняется неравенство |fXx)X + f 2(x)(1 - X)| < ф(x), при          fXx) > f,(x)          справедливо          неравенство f Xx) <| f Xx)X + f 2(x)(1 - X)| < f 2(x).

Необходимо показать, что выпуклое множество L является равномерным ретрактом. Для любого x е X определим некоторое отображение r : C_p ( X ) ^ L , такое что r ( f )( x ) = f ( x ). Функции f ( x ) е C_p ( X ) и f ( x ) >  0. Рассмотрим случаи:

• 1)    Если | f ( x )| <  ф ( x ), то r ( f )( x ) = f ( x ).

• 2)    Если f ( x ) >  ф ( x ), то r ( f )( x ) = ф ( x ).

• 3)    Если f ( x ) <- ф ( x ) 1, то r ( f )( x ) = - ф ( x ).

Нетрудно видеть, что наше полученное отображение r является непрерывным. Следовательно, по определению ретракта, выпуклое множество L является равномерным ретрактом в пространстве Cp ( X ). Теорема доказана.

Определение 4. [1] Пространство X обладает свойством Бэра, если в нем пересечение любого счетного семейства открытых всюду плотных множеств является всюду плотным.

Предложение. Если C p ( X ) пространство со свойством Бэра, то каждое ограниченное в X множество конечно.

Доказательство. Допустим, что существует бесконечное неограниченное множество A с X . Положим G i = { f е C p ( X ): существует x е A, такой, что f ( x ) >  i }, i е ¥ ⁺ , и покажем, что G i открыто и всюду плотно в C p ( X ).

Пусть f е G i . Возьмем x е A , такой, что f ( x ) >  i . Положим £ = f ( x ) - i и рассмотрим стандартное открытое множество W ( f , x , £ ) в C p ( X ). Очевидно, f е W ( f , x , £ ) с G . Следовательно, G i открыто в c p ( X ).

Пусть W ( g , x 1 ,..., x k , £ ‘ ) - любое стандартное открытое множество в C p ( X ). Так как множество A бесконечно, найдется у е A \{ x 1 ,..., x k }. Существует функция f е C p ( X ), такая, что f ( у ) > i и | f ( x i ) - g ( x i )| < £ ‘ при всех i = 1,..., k . Тогда f е G i n W ( g , x 1 ,..., x k , £ ‘ ). Следовательно, G i = C p ( X ). Покажем, что n { G i : i е ¥ ⁺ } = 0 . Пусть это не так, и f е n { G i : i е ¥ ⁺ }. Тогда для каждого i е ¥ ⁺ найдется точка x i е A , такая, что f ( x i ) >  i . Значит, функция f не ограничена на A , в противоречие с условием. Следовательно, n {G i : i е ¥ ⁺ } = 0 , что невозможно, так как пространство C p ( X ) обладает свойством Бэра.

Лемма 2. Пусть X дискретно и счетно. Тогда R X есть абсолютный ретракт в классе всех нормальных пространств.

Доказательство. Предположим, что R X есть некоторое подпространство нормального пространства Y . Рассмотрим семейство тождественных отображений t : R X ^ R X . Семейство t есть диагональное произведение вещественных функций, каждое из которых по теореме Титце-Урысона [3] можно непрерывно продолжить на все пространство Y . Данное декартово произведение тождественного отображения t есть ретракция пространства R ^X .

Теорема 3. Пусть множество Г бесконечно и U есть единичный шар в пространстве 12(Г). Вложим 12(Г) в пространство Rr (т. е. в простран- стве 12 (Г) будем рассматривать топологию, индуцированную из пространства >Г). Тогда естественная ретракция

• r : 1 ₂ ( Г ) ^ U не является непрерывной.

Доказательство. Заметим, что если мы наделим гильбертово пространство 1 ₂ ( Г ) нормированной топологией, то отображение r является непрерывной ретракцией.

Рассмотрим отображение:

• r : 1 2 ( Г ) ^ U , в том случае, когда пространство наделено топологией поточечной сходимости.

Окрестность элемента х имеет вид :

W ( х , / 1 ,..., Y n , 5 ) = { У : | х ( y ) - У ( Y / )| <  5 , i = 1,..., n } .

А окрестность образа r ( х ) имеет следующий вид:

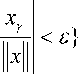
^{W (} r ^{( х} ), a , £ ) = ^{ z G L 2 ^{( Г ):} z a

Ограничимся предбазисной окрестностью (т.е. всякая окрестность есть пересечение окрестностей такого вида).

Элемент r(х) принадлежит пространству 12(Г), следовательно, xx

r ^{( х )(} a ) = _О = .        , где ^х = ^{( х} а ) _{а е} Г

11 х|1

γ ∈ Γ

Имеем

r ( W ( х , Y 1 ,..., Y n , 5 )) = { r ( У ), У G W : | х Y ) - У ( r _z )| <  5 ,i' = 1,..., n} =

= { r ( У )( в ) = , ^Ув 2 }.

∑ y β β ∈ Γ

Покажем, что не существует конечного набора Y i , Y ₂ ,..., Y n , такого что

• (*)              r(W ( х , Y 1 ,..., Y n , 5 )) с W ( r ( х ), а , £ )

Так как в окрестности W(r(х), а, £) образа r(х) фиксируем только одну координату и в сумме ряда нормы участвуют координаты х , то в окрестности r(W(х, Y1,..., Yn, 5)) прообраза фиксируется конечное число координат и в сумме ряда участвуют координаты У . Ограничения накладываются только на конечное число координат, а остальные координаты могут изменяться как угодно. Мы можем заставить координаты у изменятся так сильно, что они не войдут в окрестность W(r(x),a,ε). Следовательно, формула (*) не верна. Теорема доказана.

Замечание. Отображение r конечно же является непрерывным в топологии нормы.

Заключение

Доказано, что не существует линейного проектора первого класса Бэра пространства D [0,1] на пространство C [0,1] . Следовательно, так как не существует проектора первого класса Бэра, то нет необходимости исследовать свойства показателей Ляпунова при условии существования проектора.

Рассмотрены случаи существования равномерно-непрерывных ретрактов в пространстве C_p ( X ). При этом доказано, что выпуклое множество

L={f∈Cp(X):f(x)≤ϕ(x)} является равномерным ретрактом пространства Cp(X). Доказано, что естественная ретракция

r : l ₂ ( Γ ) → U не является непрерывной .