О векторизации алгоритма Монте-Карло решения классического уравнения Больцмана

DOI:

Метод Монте-Карло является одним из популярных методов решения уравнения Больцмана и вычисления кинетических коэффициентов в твердых телах. Несмотря на то что появился он давно, до сих пор остается одним из самых популярных методов расчета характеристик твердых тел (см., например, [4-6; 8; 9; 12] и литературу в них). Важным вычислительным преимуществом этого метода перед другими является хорошая возможность распараллеливания, особенно в случае исследования систем, которые предполагаются однородными, что позволяет не решать в процессе моделирования уравнение Пуассона для определения полей, наведенных градиентами плотности заряда.

• 1.    Описание методики квазиклассического моделирования методом Монте-Карло транспортных свойств полупроводников

во внешних полях

В случае когда пространственной неоднородностью образца и внешних электрических и магнитных полей можно пренебречь, процесс моделирования можно описать следующим образом. Будем следить за одним электроном, движущимся в электрическом поле и могущим испытывать рассеяние на неоднородностях кристаллической решетки. Предполагаем, что в промежутках между столкновениями движение частицы подчиняется законам классической механики и описывается уравнениями движения

^=еЕМ            (1)

где е — заряд электрона; Е_Х,Е_У — компоненты вектора напряженности электрического поля; р_х,р_у — компоненты вектора квазиимпульса электрона. Для определенности будем рассматривать двумерный образец. Промежутки времени между столкновениями, а также конечный импульс, приобретаемый частицей после столкновения, будем моделировать случайными величинами, закон распределения которых будет определяться вероятностями перехода из одного состояния в другое в результате рассеяния. Сами вероятности перехода рассчитываются из квантовомеханических соображений. Рассчитав для одного электрона компоненты импульса в каждый момент времени (с учетом движения в электрическом поле и рассеяний), вычисляем скорость в каждый момент времени. Многократно повторив такой расчет для различных начальных условий (можно сказать, для различных частиц), а затем, усреднив по всему набору начальных условий и по времени, получим выражение для любых кинетических коэффициентов.

Область применимости такого подхода определяется областью применимости кинетического уравнения Больцмана (см., например, [1]). Именно характерное время t, на котором рассматривается изменение волновой функции электрон-фононной системы, когда гамильтониан электрон-фононного взаимодействия рассматривается как возмущение к гамильтониану системы невзаимодействующих электронов и фононов, должно значительно превышать характерное время, определяющее динамику столкновения электрона с неоднородностями кристаллической решетки. В [1] показано, что должно выполняться условие t » 7г/ё,                                          (2)

где г — характерная энергия электрона. Выражение (2) можно понимать так. В интеграле столкновений в вероятности перехода из одного состояния с энергией е в другое состояние с энергией е' стоят дельта-функции 5(е — е'), выражающие закон сохранения энергии. Чтобы можно было хотя бы приближенно говорить о сохранении энергии при столкновении электрона с рассеивателями, необходимо, чтобы неопределенность энергии Tift была значительно меньше характерного значения энергии электрона е, откуда следует неравенство (2). С другой стороны, хотя бы потому, что в первом приближении теории возмущений не учитываются повторные акты рассеяния, которые с большой долей вероятности должны произойти спустя время порядка времени свободного пробега т, должно выполняться условие t < т.                                         (3)

Следовательно, для невырожденного электронного газа условие применимости рассматриваемого подхода т > кТ,                                  (4)

где к — постоянная Больцмана; Т — абсолютная температура.

Найти время свободного пробега можно, используя следующие соображения, изложенные, например, в [2;3]. Предположим, что, во-первых, вероятность электрону испытать столкновение (рассеяние) в течение интервала времени dt пропорциональна величине этого интервала, и, во-вторых, вероятность столкновения в единицу времени не зависит от времени. Пусть w(t) — вероятность того, что частица двигалась без столкновения в течение промежутка времени (t₀, t₀ + t). Рассмотрим событие С, состоящее в том, что электрон двигался без рассеяния в промежутке (to, to + t + dt). Это событие можно рассматривать как совокупность двух событий: события Л, состоящего в том, что электрон двигается без рассеяния в течение промежутка времени (to, to + t), и события В, состоящего в том, что электрон двигается без рассеяния в промежутке (to +1, to + t + dt). Поскольку мы предполагаем, что вероятность свободного движения частицы зависит только от длительности промежутка времени, но не от начального (или конечного) момента промежутка времени, то события Л и В независимы. Поэтому

w(t + dt) = w(t) • w(dt).(5)

С другой стороны, w(t + dt) = w(t) 3——dt.(6)

dt

Вероятность свободного движения за время dt можно выразить через вероятность рассеяния W за то же время:

w(dt) = 1 — Wdt.(7)

Для w(cZt) получаем следующее уравнение:

w(t) + -^dt = w(t)(l — Wdt).(8)

Решением уравнения является функция

w(t) = А ехр(—Wt).(9)

Здесь А — некоторая постоянная. Величина w(t) — вероятность того, что частица двигалась без столкновения в течение промежутка времени (t0, to + t), или, говоря другим языком, вероятность того, что среднее время свободного пробега т оказывается больше, чем t. С другой стороны, стандартным образом можно ввести интегральную функцию распределения F(t), равную вероятности того, что среднее время свободного пробега т оказывается меньше, чем t. В этом случае, очевидно, w(t) = 1 — F^t). Должны выполняться условия F(0) = 0, F(oo) = 1, откуда А = 1. Рассмотрим величину /(£) = dF/dt — плотность вероятности распределения случайной величины — времени свободного пробега частицы. Выражение для f(t) имеет вид:

f(t) = Wcxp(-Wt).                         (10)

В выражении (10) W — полная вероятность рассеяния носителя заряда в единицу времени. Эта вероятность зависит, прежде всего, от величины квазиимпульса электрона в момент времени рассеяния: W = РИ(р). Величина Wt, стоящая под знаком экспоненты, фактически определяет вероятность рассеяния носителя заряда за промежуток времени длительностью t. При помещении образца в электрическое поле электрон между столкновениями движется согласно уравнениям движения (1), так что импульс, а с ним и вероятность рассеяния начинают зависеть от времени. Обобщение выражений (9), (10) на этот случай состоит в заменах р^-р№ = р + |а^)                   (И)

t

(А.^ = —с J Е^) dt) — вектор-потенциал), о

t

Wt^ j W(p(t'))dtF(12)

о

Так что вероятность того, что электрон не испытает столкновения в течение промежутка времени t при движении под действием внешнего поля, имеет вид:

t                        / t'\

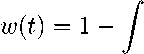
РИ(р(^))ехр I — j W(p(t"))dt" j dt'.(13)

о                  \ о/

Выражение (13) можно использовать для розыгрыша времени между последовательными рассеяниями. Сопоставим 1 — w(t) величину г, равномерно распределенную в промежутке (0, 1). Тогда время t движения электрона под действием полей между двумя последовательными соударениями можно определить из уравнения

• #                        /     t'\

  
  
  

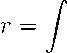
lF(p(^))exp | — I W(p(t"))dt" j dt'.(14)

о                  \  о/

Решение уравнения (14) — достаточно сложная процедура, которую к тому же необходимо проводить десятки и сотни тысяч раз во время моделирования. Поэтому для упрощения расчетов применяется, например, прием, развитый в [Ю; 11]. Введем фиктивный процесс саморассеяния, не меняющий импульс частицы [3]. Положим вероятность перехода между состояниями р и р' в результате такого процесса

1Г0(р.р\) = 1Ш^^                                   (15)

Величину Wo(p) можно выбрать произвольно, поскольку состояние частицы в результате саморассеяния не меняется. В выражении (15) Ж(р) — вероятность рассеяния, обусловленного всеми взятыми в рассмотрение процессами. Тогда с введением саморассеяния (14) преобразуется к виду:

£                                                   /     t'\ г = У (И^)) + W))) ехр - У (МрО + W0(p(t"))) dt" df. (16) о                                   \ о/

Полагая

Ж0(р(ф) = Г-Ж(р).(17)

где Г — некоторая постоянная, получаем условие для определения момента столкновения в форме г = 1 — схр(—Ft),(18)

Величина Г должна быть выбрана таким образом, чтобы в интересующей области значений импульса величина ИДр) была положительной.

Таким образом, процесс моделирования движения одной частицы описывается следующей последовательностью действий:

• 1)    выбрать константу Г из рассмотрения выражений для вероятностей рассеяния;

• 2)    определить время свободного пробега из выражения (18);

• 3)    вычислить траекторию на свободном пробеге из системы (1), используя какой-нибудь алгоритм решения систем обыкновенных дифференциальных уравнений;

• 4)    определить механизм рассеяния и новый импульс частицы после рассеяния;

• 5)    повторить пункты 2-4 нужное число раз и из сохраненных траекторий вычислить искомые параметры системы.

2.    Подходы к векторизации расчетов траекторий частиц

Из описания процесса моделирования видно, что все повторения для отдельных частиц независимы друг от друга и их можно провести в разных потоках или процессах и результаты вычислений по отдельности потом слить в единый массив данных. Однако современные процессоры являются не только многоядерными, но также поддерживают векторные операции (см., например, [7]) в пределах одного вычислительного ядра, что дает дополнительные возможности ускорения расчетов.

Речь идет прежде всего об инструкциях наборов SSE, AVX и AVX2. В последних поколениях процессоров Intel регистры AVX и AXV2 имеют размер 512 бит. Таким образом, на каждом ядре такого процессора мы можем одновременно производить действия над 16 32-битными целыми числами, или 8 64-битными целыми числами, или 16 числами с плавающей запятой одинарной точности или 8 числами с плавающей запятой двойной точности. Так как в моделировании, описанном выше, речь идет, прежде всего, о работе с числами с плавающей запятой с двойной точностью, то появляется дополнительная возможность значительно ускорить расчет траектории. Поясним на примере цикла расчета траектории очередного пробега частицы в постоянном поле силы Fx методом Эйлера (разумеется, что в этом случае траектория вычисляется и аналитически, но для простоты изложения нужен как раз простой пример). Допустим, в момент времени to частица имеет проекцию импульса рхо- Время следующего пробега до столкновения обозначим At. Получим цикл, подобный нижеприведенному double t = tO; double px = pxO; while(t < tO + delta_t) { px += Fx*dt; t += dt;

}

Видно, что по структуре цикла операцию px += Fx*dt можно векторизовать, выполнив необходимые арифметические действия сразу над 8 числами. При этом, конечно, значение рх превращается также в вектор из 8 чисел. Таким образом, при векторизованном расчете траекторий пробега мы работаем сразу с 8 частицами на одном вычислительном ядре.

Саму векторизацию можно произвести несколькими общеизвестными способами. Прежде всего это:

• -    использовать специальные ключи и директивы компилятора;

• -    использовать возможности Array Notation и Elemental Function в рамках технологии Intel Cilk Plus для компиляторов Intel;

• -    использовать классы интринсиков;

• -    использовать векторные функции-интринсики.

Каким способом это делать, принципиально не важно. Отметим, что каким бы способом реализации расчета траектории не воспользоваться, ускорение будет, конечно, не восьмикратным из-за того, что в векторные регистры данные нужно сначала загрузить и после расчета выгрузить.

Также необходимо решить еще одну проблему. Для разных частиц времена пробега At выбираются случайным образом из выражения (18). Но для того, чтобы получить полный выигрыш от векторизации, необходимо, чтобы количество итераций представленного выше цикла для разных частиц было одинаковым, а значит были одинаковыми и времена At. Для того чтобы выполнить это условие, расчеты времен пробега нужно сделать двухстадийными. Отметим, что, во-первых, так как выбор времени пробега по формуле (18) не зависит от текущих импульсов частиц во время моделирования, то логично делать выбор сразу всех значений At для всего интервала модельного времени для каждой из 8 частиц. И, во-вторых, в любом месте моделирования мы можем вставить процесс саморассеяния, так как фактически он не изменяет состояния частицы и, значит, не изменяет никакие рассчитываемые физические величины. С учетом сделанных замечаний алгоритм выбора промежутков пробега для массива из 8 частиц, расчет траекторий которых будет векторизоваться, можно представить в виде следующих двух этапов:

• 1)    Для каждой частицы выбираются времена пробега согласно (18).

• 2)    Для любого момента времени, когда хотя бы одна частица имеет рассеяние, добавить к тем частицам, которые не рассеиваются в этот момент времени, процесс саморассеяния. Таким образом, формально все частицы будут иметь один и тот же набор времен пробегов, и цикл, решающий уравнения движения, для каждой частицы будет всегда иметь одно и то же количество итераций.

Для оценки эффективности предложенного метода ускорения расчетов кинетических коэффициентов твердых тел методом Монте-Карло нами был проведен ряд численных экспериментов для различных механизмов рассеяния носителей тока. Цикл, в рамках которого решаются уравнения движения, векторизовался с помощью применения интринсиков. Часть моделирования, где выбираются импульсы частиц после рассеяния, не векторизовалась (это является темой отдельного исследования), поэтому различные механизмы дали различное ускорение расчетов из-за различной сложности их расчетов. В среднем мы увидели ускорение от 10 до 30 %, что, как нам кажется, является хорошим результатом. В дальнейшем предполагается улучшить его с помощью векторизации выбора импульсов после рассеяния и обработки результатов.

Заключение

Моделирование методом Монте-Карло транспортных свойств полупроводниковых материалов позволяет получить решение задачи без непосредственного решения интегро-дифференциального уравнения Больцмана, что позволяет использовать этот метод для независимой проверки выводов аналитических расчетов, выполненных с использованием модельных интегралов столкновения. Актуальной задачей является ускорение расчетов кинетических характеристик материала с использованием метода Монте-Карло, которое может достигаться использованием различных технологий распараллеливания, а также векторизации расчетов. Использование векторизации позволяет в полной мере задействовать ресурс современных процессоров, применив для вычислений длинные регистры. В настоящей работе обсуждается возможность векторизации решения уравнений движения частиц. Показано, что использование интринсиков позволяет получить ускорение от 10 до 30 %.