О влиянии близости источника дилатационных волн на динамические напряжения цилиндра с жидкостью

Как известно, подземные трубопроводы при сейсмических воздействиях подвергаются колебаниям, которые сопровождаются большими повреждениями и даже отказом целой системы [8, 9, 10, 12, 17, 18]. Исследованию состояния подземных трубопроводов при сейсмических воздействиях посвящено множество работ [2, 3, 4, 5, 6, 7, 11]. В этих работах падающая волна напряжения считалась плоской. Однако для источников, расположенных близко от оболочки, возникла необходимость исследовать вопросы близости источника (на результаты работ) [15, 16]. В данной работе исследуется взаимодействие цилиндрических волн напряжения с цилиндром, состоящей в общем случае из конечного числа коаксиальных вязкоупругих слоев.

Постановка задачи

В работе исследуется взаимодействие цилиндрической волны напряжения параллельно-слоистыми упругими слоями с жидкостью. Предполагается, что линейный источ- ник (см. рис. 1) является непрерывным источником дилатационных волн напряжения с угловой скоростью ю и амплитудой ф0, а слоистый пакет представляет собой толстостенные и тонкостенные слои цилиндра. При описании движения тонкостенных элементов используются уравнения теории таких оболочек, в основу которых положены гипотезы Кирхгофа– Лява. Для тонкостенных слоев исходными являются уравнения линейной теории упругости. Нумерация слоев – произведение в порядке возрастания их радиусов от k =1 до k = N (рис. 1).

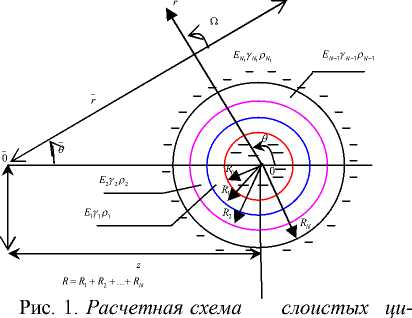
линдрических тел, находящихся в деформируемой среде

Величине, характеризующей свойства и состояние элементов, соответствуют значения j =1, 2, 3,…, N , где К – упругий слой заключен между ( К –1)-м и К -м слоями. Параметры среды обозначены индексами К=N (рис. 1).

В предположении обобщенного плоско деформированного состояния уравнение движения в смещениях имеет вид [1]

~__ _       ■ d u j

( A j + 2 Д j ) grad divu j — fi rotrotu j + b_j = p j    ₂ j ,

(1) где A j и ^ j ( j = 1,2 ... N , j = N относятся к

d v o d r

^r = R o

^{d u}r 1 d t

r = R o

где u_{r 1} – перемещения слоя по нормали.

На контакте двух тел (при r = R j ) выполняется равенство смещений и напряжений (условие жесткого контакта)

окружающей среде, j = 1,2,

...

, N — 1 - к слою)

операторные модули упругости [13]

j ( t ) = A oj

t f (t) — f R')(1 — w

t

—

Т ) f (Т ) dT ,

t— j f ( t ) = p 0 j f ( t ) — f R^(t

—

^T ) ^{f ( т} ) d ^T ;

_           — w                            _

^

b_j – вектор плотности объемных сил; f ( t ) –

некоторая функция; ρ _j

urj = ur (j+1); ^rrj = ^rr (j+1), ue j = ue (j+1); ^rej = ^re (j+1)-         (4)

Отметим, что в случае скользящего контакта грунта по поверхности трубы последнее уравнение в (4) примет вид [1]: o_rej = o, где < 7^J_n ) и ^n^]_s ) - радиальное и касательное напряжения в j -го вязкоупругого тела; u_n ^{( j )} и u ⁽ _s ^{j )} – радиальное и тангенциальное смещения j -го тела. Решение волнового уравнения (1) в потенциалах перемещений удовлетворяет в бесконечности (при r → ∞) условию излучения Зоммерфельда [14]:

–

плотности мате-

риалов, R¹ ) ( t — т ) и R ^ ‘ ) ( t — т ) - ядро релаксации, λ_oj , µ_oj – мгновенные модули упругости вязкоупругого материала, u j ( u j , u ^ ) - вектор смещения, который зависит от r , θ , t . При давлениях до 100 МПа движение жидкости удовлетворительно описывается волновыми для потенциалов скорости частиц жидкости [14]

lim ⁽Pn = ^o,

r ^Ю

N

r ^w

r ^w

_у d r

^{+ ia}V N

lim W n = ^o,

r ^»

N

у d r

= o

,

A

^{+ в} W n

= ^o- (5)

^A V o =

1 ^d V o

d2    d где A = —2 +---+ dr2 rdr

^Со ² d ² r ² d θ

d t ²

,

₂ ; С о – акустическая

скорость звука в жидкости. Потенциал ϕ ₀ и

вектор скорости жидкости связаны зависи-

^

мостью V = gradv ₀. Давление жидкости (при r = R ₀) определяется с помощью линеаризованного интеграла Коши–Лагранжа, ' °

Р = — рос0 —— - давление жидкости на dt стенке цилиндрического слоя и ρо – плотность жидкости.

При условии безотрывного обтекания жидкости нормальная компонента скорости жидкости и слоя на поверхности их контакта (при r = R 0 ) должны быть равны

Рассмотрим продольную волну, порождаемую продольным источником волн расширения, расположенным в точке О . Потенциалы перемещения падающей волны расширения можно представить в виде [16]

V N = P NO^ H O^N r ) e" "  , (6) где Н о ⁽¹⁾ – представляет собой расходящиеся функции Ханкеля (первого рода нулевого порядка); ϕ_NO – амплитуда волны расширения; a _N - волновое число сжатия; a N = м ²/с² _а , м

– круговая частота.

Методы решения

Поставленная задача решается в потенциалах перемещений, для этого представим вектор перемещения в виде:

u j = grad p + roty .j , ( j = 1,2,......., N ) ,

где ϕ _j

–

потенциалы продольных волн;

ψ j ( ψ rj , ψ θ j )

–

потенциалы векторного

от by (a) = JR^j (t)cosar dT .

поля поперечных волн.

Основные уравнения теории вязкоупругости (1) для этой задачи плоской деформации сводятся к следующему уравнению:

Решение уравнения (7) с учетом (9) выражается через функции Ханкеля 1-го и 2-го рода n -го порядка:

( У + 2 j %,

t

—

^— y J Ret ^{— r} fi jr ^— 2 ^ J R J ^{j ) ( t — r} ^j d? = ,

t

v , = X^[ AH ( ar ) ⁺ AH? (ar ^{)] cos n 0 e} n =0

V j = X [ B nj H'ar ) + BH er ) ] sin & n =0

₍— iat ,

₍— iat „

—от

⁰²V j

= ^P J rP , d t

—от

t

JojV Vj — Joj J Rj)(t — T)V V jdT = Pj

—от

d V j dt²

,

d2    1 d где V = —2- +--+ d r    r d r

1

d ²

d 02

– диф-

ференциальные операторы в цилиндрических координатах и v_j – коэффициент Пуассона [1].

На бесконечности, т.е. при r → ∞, потенциалы продольных и поперечных волн при j = N удовлетворят условию излучения Зоммерфельда (5). Решение уравнения (7) можно искать в виде:

от

от

iat; , j (r, 0 , t) = (8)

— i a t

,

( ϕ )                  ( ψ )

где q_kj ( r , θ ) и q_kj ( r , θ ) – комплексные функции, которые являются решением следующим уравнениям, вытекающим из (7):

V^ ) ( r , & ) + a q . >  = 0, V ²q , ) ( r , & ) + e 2 q , ) = 0,

² ( V )(г 1+^²а ⁽⁹

2 =     ,        .pa2    ,        , j   yoj(1—yoj)+ 2a(1—“Oj)

2      ρω ²

j “ J F ^ OJ )

₂    ω ²

^a 0 = ^;

С ₀

^Oj = ay (a) + ib^j (a), “j = a,. (a) + ibj (a), от

ayj (a) = J Ry (r )sin ar dr ,

n =0

V n = X [ M nN H ^¹ ( P N r ) + L H ( er ) ] sin n&e ■ , n =0

V 0 = X ^{[ K}n 0 J n ^{( a} 0 ^{r ) +} K ‘ 0^Nn ^{( a} 0 ^{r )] cos n 0 e — a t} , n =0

где A nj , A nj , B nj , B nj , C nj , d ,, L nN , M nN , К nN и K' n _N — коэффициенты разложения, которые определяются соответствующими граничными условиями; H_n ⁽¹⁾ ( α _jr ) и H_n ⁽²⁾ ( α _jr ) – соответственно функция Ханкеля 1-го и 2-го рода n -го порядка

Hni),(2) (ar ) = Jn (ar ) ± iNn (ar ) .

Решение (9) при j = N удовлетворяет на бесконечности r →∞ условию излучения Зоммерфельда (5) и представляется в виде:

от

V n = X ^CnN^{H1 ( a} N^r )^cos( m ^{0 )} e ^{— i a t} ;

т = 0

от

,N = X MnNHn ^Nr )sin( n0) e т=0

, — iat

Решению задачи (2) при r ^ 0 удовлетворяет условие ограничения силовых факторов [1] и отсюда следует, что К'_п = 0 :

от

V 0 = X ^Kn 0 Jn ^{( a} 0 r ^{) cos} n&e n =0

,— iat

Полный потенциал можно определить путем наложения потенциалов падающих и отраженных волн.

Таким образом, потенциалы смещений

будут

фN = VNp) + Vn , ^N = Vn , Ф = Vj, j ,j, ф0 = V0. (10)

Для определения напряженно-дефор-мируемого состояния сначала необходимо выразить падающую волну через волновые функции (10). Используя геометрическое построение на рис. 1 переходим от координат r • 0 к координатам r , 0 в области r <  r_N .

? Np ) = E 0 in .

от

U9i = r -1У θj n=0

" A_n j E ^j a r ) + ⁺ A j E60^ ) + B_n j E ^j P r )

1+

+

sin n θ e

+ в ^64^ ) _

% EiE a r ) +

— i

i ω t

^, (12)

от

Ё ^{[( — 1)} n^En^Jn ^{( a} N^r ) H^ ^{( a} N z ^)] cos ^{n 0 e} n =1

— i"'

,

& 0 N = ² P N ^{( 1 — M} kN ) ^Г — Ё ^{+ C} nN ^E 21 ⁾⁽ « N r ^{) +} cosn ⁰ — •

где E_n

= s

[ 1, n = 0 _т

, J – цилиндрическая 1 2, n >  1 n

" [+MnET ■ ) J от %EniEN)(aNr)+

- N = 2 e n ( 1 — M'n ) r ^{— 2} Ё + C N E 43 ^N KcNr ) + sin n 0 e " ,

n = 0

функция Бесселя первого рода.

Отсюда следует, что напряжения и смещения легко могут быть выражены через потенциалы смещений [2]:

U ■ rj

д ф:    1 д V i

—~ + ■; u _{0 j} д r r д 0

1 д ф0   д V o

—

r д 0      д r •

σ rrj

= Л V ² Ф j + 2 P j

д ² ф j д r²

д ( 1 д V , + — I .

д r к r д 0

;

σ θθ j

= Л V ² ф _j + 2 p _j

1₍ ф ₊ 1 д ф ) ₊ r д r r д 0²

₊ 1(1 Oj r r д 0

—

^{д 2} V j )

д r д 0

; ( 11 )

σ r θ j

—

X д Ф j r ² д 0

+

^rrj = 2Я 11  Mkj]r 2 Ё n=0

[+ M nN E 432 ^N ) ( p t ) Aaar ) + + A ^E ■ a r ) +

' + BE^r ) + _ _ B l El^r ) .

cos n O e i"’ ,

^00 = 2я1 Mjr—2 Ё n=0

AEaf+ . + Aaas ) ¹ + B^^pr )• _+ B j^jj r )

'+

■+

cos n 0 e ‘ " t ,

^ = 2Ej(1—MY—2 Ё n=0

A j E a ar ⁾⁺ .⁺ A j E ^j \jr ⁾⁺ ' + B E 4>r ) +

sin n 0 e ‘ " t •

= E [21-   ф r д 0д r

, ■ 1 д 2 v j j( 1 д v j 3	+ в^в ) _
r2 д 02      д r к r д r J                       где 1      22a Далее, подставляя (10) в (11) с учетом    e ( 'j ) = n 2 + n — P j (9), получим следующие выражения для пе-    11              2 ремещений и напряжений:                     eJ = n [( n + ^( j от Ф 0 En i E 51 H ^ N r )+                          I         p uN - r 1 Z1 C nN E 53 N )( a «r )+ cos n e e " •      E 2 k'j = n + n + 2 ' =0 +M E°NЧв 4                     к L + M N E 52 e Nr ) J           + a jj r ) • от Г ^ 0 EXE 6; ‘ ) ( » Nr )+ ]                E 2 k( )= nPrYEp u. = - — l Z + C nN E 63 N ) ( a , r ) + cos n 0 e — " ,                  1 n =0                         \                                    kj ) - a r2- + M, N E 63 N ' ( Р . п )                         E 31 = “ j r к Г A^ j r ) +      1           E 4 k ’ = n [( n + ^E	Y ka r P r ) + в 2 r 2       2 --a, r ir )— ( n + 2 в j r	— a jr Y np a j r jE — } Pr ) ] • 2 Y nk a ) + J 1 ) Y n' k) P j t ) ] • Y "br ) . /yEP jr ) ] >
	2 J a jt- ) — a

)• от

—I

E ^{( kj} ) - ^E 42

cos n0e ^{— i} " •

u rj = r

z + j4j ar)

+

n = 0

+ в„Е ,3^j ) вг ) + в' . E 2^j

—

n 2 + n —

к

EE 3

2 J

^jf ) + e j rH n 'в , )

E 5 ? М “ Л- 1 ' ( “ j r ) - nY nkjj )] , E W=- nY nkj ' ( fi r ) , E 6 ? ' = - nY n^kj ' ( a r ) , E 6 k ' = И в ) - PrY n - в ) 1 k = 1.2.3.4,

Q 2 N ( e N R N ) = ( n ’ - n + 1 в Ав^АвЛ ) -

C ²

2          1      2   2      2    2   (1)                 2 pN

⁽ n ⁺ n P_N ^rn )P_N ^rn ^{h n} [ P N R N ) , k N = 2

4                            C_SN

.

где

Y(1 J) = J    Yj)Jj = N n            n, n             n,

Y ( 3 J ) = //( 1 ) y( ⁴ J ) = 12^

¹ n ¹¹ , , n n          ¹¹ . •

Построение формального решения не встречает принципиальных затруднений, но исследование такого решения требует огромного количества вычислений. Задачи сводятся

Теперь рассмотрим некоторые предельные случаи.

При r ^ 0 :

H¹’^z ) ^ =±— In z - i I-l 11— In z j+ 0 ( z ⁴ln z ),

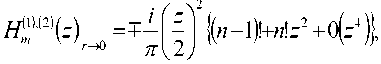
и r ^w :

e ± i ( kz - n /4 )

к решению неоднородных алгебраических уравнений с комплексными коэффициентами.

[C]{q}={p}, (13) где { q } – вектор-столбец, содержащий произвольные постоянные; {F} – вектор-столбец внешних нагрузок; [C] – квадратная матрица, элементы которой выражаются через функции Бесселя и Ханкеля. Уравнение (13) решается методом Гаусса с выделением главного элемента. В работе перемещения и напряжения сводятся в безразмерных видах:

H

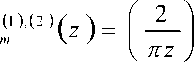
использованы асимптотические формулы

Ханкеля 1-го и 2-го рода [14]. Если в выражении (14) Z стремится к бесконечности, то

можно воспользоваться асимптотическими

разложениями функции Ханкеля для больших значений аргумента [10] ( a - конечное):

* u r ^* j

u rj ; i αϕ _A

* u _{θ j}

u θ j ; i αϕ _A

*

σ rrj

σ rrj

;

σ ₀

^lim z H« ° ее

r = ^r n ~ 4

1 - ¹ If ^{+ 1} E nkN cos n 0 e- i ^w .(15) k N _ n = 0

w

*      σ r θ j                   2

° е = —-;   ° 0 = ^- vP 9 a .

σ ₀

В случае, когда E₁=E2^=E_N, p i= p 2...= p _N и v ₁= v ₂.= v _N , получаем отверстия (r=R), находящиеся в безгранично упругой среде ( a_N ( w ) = 0 , b_N ( w ) = 0 ). Граница (r=R) сво-

Это выражение полностью совпадает с выражениями, полученными в работе [10] для плоской падающей волны. Если волновое число стремится к нулю, тогда предельный процесс

описывает статическое решение для длинных волн. Этот предельный процесс позволяет нам

бодна от напряжений, т.е. жидкость отсутствует. В этом случае окружное напряжение на поверхности полости сводится к следую-

использовать аппроксимирующие выражения для функций Ханкеля при малых значениях аргумента (Z – конечна):

lin^ ° ее

r = R 1

4 ^{1 + (} R N ^{) 2} + Z ^ * DK ,

щему:

(n \ — 4/1 2 Г,     1

° 99 N ^{( R} P t ) =     ^e N ^ N ^ O I ^{1 —}~z

П        <   k

w

*^(-1)n en H(1)n(aNZTN cosnde’w n=0

w где DK = ^(-1) m-2(- RN) m-2( m - 1)cos me. z

где

^TnN = k N R N ) = [^a N R N ^H n-1( ^a N R N ) ^- H - 1( ^a N ^R ) + Q N[PAl ^)] ,

Это решение точно совпадает с решением статической задачи, полученным в работе [16]. Если в цилиндрической полости содер-

жать идеальную жидкость, тогда кольцевые

Q nN ( e N ^ N ) =

Q (P n R n ) Q : N 'в R ) ,

Q 1 n ( PA ) = ( n ² -1) PAH “’ n - 1 ( e N R N ) -- ( n ² - n + 2 Pn^^ H¹ ( e N R N )

напряжения примут вид:

.   4    i ^{n +1} / 1     nfaR /      2 /2     $R Y

°e =-1XX {[   -1 7 (n-1)-n2 (n    n : l+ nn= 4  < An a 2               4 у

+ ^в R n [ n ( n + 1 ) - 2 e N R ² у I n ( a r ) H n ( в r ) +

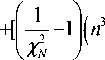
- n ² - n ) - 4 n ^ N R в RI ( a R ) H n - 1 ( P n R ) +

+

Г1

л

-1

n - .+1 вR ]«Л-1 (aR) H. W )+ 2     7

При a 1 R — 0 получается решения ста-

тической задачи

+

Г

— -11(1-n2) авRI.-1 (a, R) H_i(fiNR)}cos nOe-M, к XN  7

orr =—-—;

A) +R N u

2 A (1- V )Л /      \

—0(—1 ) - ( 2 - 4^ ) cos2 O A o + R n Г   N .

где _y 2- 2 ^{( 1} v ^N ) ₌ ^L    _n R .

χ _{N                  2} ; η

В предельных процессах выражения (15) и (16) описываются физическими результатами, приведенными в таблице.

¹ - ² v N     ^a N          ^p N

Сведения о предельных процессах

Случай 1	Случай 2	Случай 3	Случай 4
Й1Ы r = R } α – произвольная	^Ш. R ) z – конечно	limKl r = r } a —— 0	lim|im & OO   I a —0 r —w     r = R α – конечно
Динамическое решение для плоской волны.	Статическое решение, линейный источник волн расширения	Статическое решение, напряженное состояния чисто сдвига.	Статическая задача о плоском деформированном состоянии

Коэффициент концентрации напряжения

& O _{O N} определяется следующими формулами

* σ θθ

σ θθ

^r = ^R N

r = ^R N

σ

( p ) θθ

где o Oe ) = i пф ₀ Ц a ² [Н₂⁽¹⁾ яфц (( а r ) +(1- k ²) H₀⁽¹⁾( a r )] e -i“t .

Если учитываем жидкость, тогда с помощью (2), (3) и (12) можно определять соот-

*             *

ветствующие напряжения σ_rrN и σ_θθN

Числовые результаты

Для данных падающих волы напряжения и смещения определяются рядами, описываемыми выражениями (10)–(14) в случае жесткого контакта. Вычисления были выполнены на компьютерном программном комплексе "Matlab", ряды вычислены с точностью до 10-8.

Все выражения для напряжений и смещений имеют вид:

(R + i Im)e-iwt = (R2 + Im2 )1/2 e-i(wt-Y). (18)

Как видно, решение поставленной задачи выражается через специальные функции Бесселя и Ханкеля 1-го и 2-го рода. С увеличением их аргумента ряды (10)–(14) сходятся. Поэтому, на основе численных экспериментов установлено, что учет 5–6 членов рядов достигла точности 10-6 – 108.

A = 0,048; в = 0,05; a = 0,1.

Для исследования концентрации напряжений на свободной поверхности воспользуется абсолютные значения комплексной величины и соотношения (15) и (16). Ком-

плексная функция зависит от волнового числа a , угла 0 расстояния r , коэффициента Пуассона, модулей Юнга, плотностей, геометрических параметров R и Z.

Если все характеристики (рис. 1) механической системы одинаковы (Е 1 =Е₂= . E n ; p i = p 2 =. . .= p n ; V 1 = V 2 = V 3 =... = V n ), тогда рассматривается задача взаимодействия цилиндрических волн с цилиндрическими полостями. На рис. 2 приведена эпюра коэффициента

* концентрации напряжения ^ oo r = R_N в зависимости от θ при

A = 0,048 ; в = 0,05;

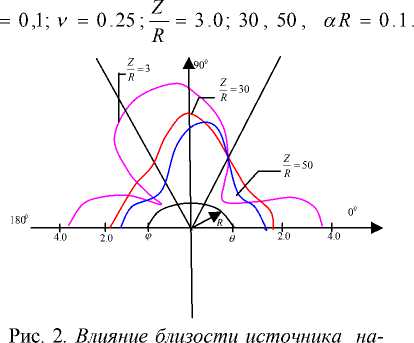
пряжений |_ст *_в    в зависимости от

О (a R = 0,1)

Из рис. 2 видно, что влияние близости источника заключается в перемещении максимального значения к точке, где прямая, проведенная из источника, касается границы полости.

Для коэффициентов концентрации напряжений будем использовать абсолютное значение комплексной величины (18).

На рис. 3 изображено изменение

*

& 99 \ r = R_N в зависимости от волнового числа

Z при различных значениях — = 6 0; 12; 20, ко-R торые быстро стремятся к решению для плоской волны, когда «R > 0.16. Это означает, что, когда источник находится на расстоянии пяти радиусов от полости, высокочастотный

*

характер изменения σθθ можно аппрокси- мировать решением для плоской волны.

Далее все значения приближаются к одной и той же асимптоте. Наибольшее различие между решением для плоской волны ( Z ^ ж ) и рассматриваемым решением имеется в интервале 0 <  «R <  0.22 .

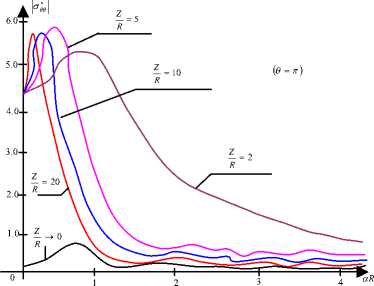
Рис. 4. Значение & >*_9в в зависимости от aR ( 0 = п )

В случае Z / R = 2 (рис. 3) кривая динамической концентрации отличается от статической до 15 %.

В случае aR = 2.0 результаты статиче-

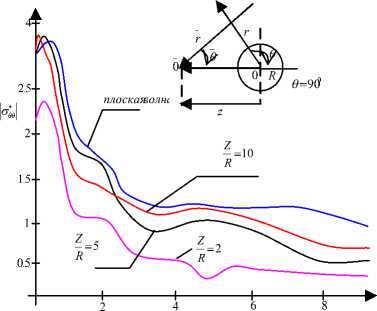
Рис. 3. & 0₀ в зависимости от a R (волновой число) при 9 = 90 0 ; A = 0,048; a = 0,1; в = 0,5

ского и динамического напряженного состояния отличаются коренным образом при близких расстояниях источника (Z / R = 2). При R1/Z > 50 воздействие цилиндрического ис- точника раскладывается как плоская волна, т.е. можно не учитывать радиус кривизны волны.

Аналогичные результаты получены для цилиндрической полости с идеальной жидкостью. Результаты расчетов изображены на рис. 5. Из рисунка видно, что значения напряжений сильно зависят от параметра

С_{р 1}

Y =---. Кроме того, имеет место резонанс-

С р 2

ное явление.

Легко видеть, что когда aR ^ 0, динамическое решение для случая плоской волны приводится к статическому значению: ( V = 0.25, 9 = п /2 ), т.е. &₉₉ =2.67.

Аналогичный, но более резко выражен-

*

ный, характер изменения отмечен для σθθ при (0 = п) (рис. 4). Когда aR > 1.0, реше- ние для динамического источника при значе-Z ниях = 5.0; 10; 20 снова сводится к реше-

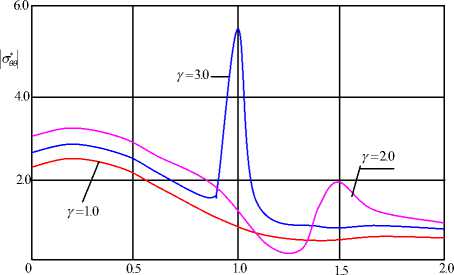
Рис. 5. Зависимость & * ₀ от a N R (Волновое число)

нию для плоской волны.

Выводы

• 1.    Задача дифракции гармонических волн в цилиндрическом теле решается в потенциалах перемещений. Потенциалы перемещений определяются из решений уравнения Гельмгольца. Произвольные постоянные определяются из граничных условий, которые ставятся между телами. В результате поставленная задача сводится к системе неоднородных алгебраических уравнений с комплексными коэффициентами, которые решаются методом Гаусса с выделением главного элемента.

• 2.    Контурные напряжения σ θθ на свободной поверхности цилиндрических тел достигают своего максимального значения в

  π

  
  

  Q = \

  
  

  π

  
  
  
  

  - при воздействш поперечных волн

• 3.    Когда источник гармонических волн находится на расстоянии пяти радиусов ( Z >  5 R ) от цилиндрического тела, высокочастотный характер изменения контурных напряжений σ θθ , воздействующих на внутреннюю свободную поверхность, хорошо аппроксимировать решением для плоской ( Z ^ от ) волны. Далее все значения приближаются к одной и той же асимптоте.

• 4.    Числовые результаты показывают, что динамические коэффициенты концентрации напряжений около цилиндрических тел зависят от расстояния между источником и телом, волнового числа для цилиндра и среды, физико-механических параметров среды и тела.

.

- при воздействш продольных волн

Контурные напряжения σ θθ при воздействии поперечных гармонических волн на 15– 20 % больше, чем при воздействии продольных волн.