О выборе начальных условий для дифференциально-алгебраических уравнений
Автор: Соловарова Любовь Степановна
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Функциональный анализ и дифференциальные уравнения
Статья в выпуске: 1, 2017 года.
Бесплатный доступ
Для применения численных методов, разработанных для систем обыкновенных дифференциальных уравнений с вырожденной матрицей перед главной частью, необходимо задавать начальное условие. В отличие от систем обыкновенных дифференциальных уравнений в нормальной форме, это условие нельзя задавать произвольно, и оно должно быть согласовано с правой частью системы. В статье предлагается алгоритм выбора недостающих начальных условий для случая, когда начальные условия заданы не стандартным образом, а представляют собой условие Шоуолтера-Сидорова. Данный алгоритм основывается на некоторых фактах из теории проекторов. Основной результат статьи проиллюстрирован простым примером.
Дифференциально-алгебраические уравнения, начальное условие
Короткий адрес: https://sciup.org/14835204
IDR: 14835204 | DOI: 10.18101/2304-5728-2017-1-18-22
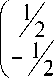
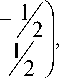
Список литературы О выборе начальных условий для дифференциально-алгебраических уравнений
- Чистяков В. Ф. Алгебро-дифференциальные операторы с конечномерным ядром. -Новосибирск: Наука, 1996. -280 с.
- Гантмахер Ф. Р. Теория матриц. -Москва: Наука, 1986. -576 с.
- Sviridyuk G. A., Fedorov V. E. Linear Sobolev Type Equations and Degenerate Semigroups of Operators. -Boston: VSP, 2003. -216 pp.
- Коновалов A. H. Задачи фильтрации многофазной несжимаемой жидкости. -Новосибирск: Наука, 1988. -166 с.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. -Пер. с англ. -Москва: Мир, 1999. -685 с.
- Brenan K. F., Campbell S. L., Petzold L. R. Numerical solution of Initial-Value Problems in Differental-Algebraic Equations -Philadelphia:Appl. Math., 1996. -270 pp.
- Бояринцев Ю. E. Регулярные и сингулярные системы линейных обыкновенных дифференциальных уравнений. -Новосибирск: Наука, 1980. -222 с.
