О вычислении функциональной производной для одной задачи оптимального управления

В современной лазерной технике, системах коммуникации, космических исследованиях и многих других областях науки и техники для управления электромагнитным излучением широко применяются многослойные дифракционные решетки [1, 2]. При этом в различных оптических системах к дифракционным решеткам предъявляются совершенно разные требования. Однако в большинстве случаев решетка должна обладать максимально возможной дифракционной эффективностью в определенных порядках дифракции. Получить требуемую характеристику можно за счет подбора формы профиля решетки, поскольку именно геометрия профиля в основном определяет эффективность, с которой свет дифрагирует в каждый из порядков [2]. Таким образом, чтобы найти оптимальные параметры дифракционной решетки перед ее непосредственным изготовлением, необходимо решить задачу синтеза дифракционной решетки.

С математической точки зрения задачи синтеза дифракционных решеток являются задачами оптимального управления и формулируются как задачи минимизации целевого функционала. Целевой функционал строится таким образом, чтобы его минимум соответствовал максимальному значению дифракционной эффективности при требуемом порядке дифракции на отражение или пропускание и при этом сам функционал зависел от геометрических параметров решетки – параметров управления. Для минимизации целевого функционала применяется градиентный метод, при котором градиент вычисляется с помощью решения сопряженной задачи [3]. Это наиболее устойчивый метод с точки зрения увеличения числа управляющих параметров, и его сходимость к оптимальному решению математически обоснована [4].

В данной работе обсуждается метод вычисления градиента целевого функционала при помощи решения сопряженной задачи с выбранными специальным образом граничными условиями.

1.    Постановка задачи синтеза дифракционной решетки

Рассмотрим одномерную многослойную дифракционную решетку, состоящую непосредственно из решетки с прямоугольным профилем штриха, подложки и системы однородных слоев, расположенной между ними (последнее, вообще говоря, не является обязательным). Решетка считается бесконечной и периодической вдоль оси x с периодом d , причем ось z перпендикулярна границам слоев структуры. Период профиля разбивается на K равных между собой подпериодов d k = d/K, как показано на рис. 1. Каждому k -му подпериоду соответствует свой фактор заполнения f _k .

г----------------------------------------------------ч dk f1d1               fkdk

n I

n III

Рис. 1 . Многослойная бинарная дифракционная решетка

Математическая постановка задачи синтеза формулируется как задача оптимального управления и заключается в минимизации целевого функционала mfin F (f), где f = (fl f2 ... fk)                         (1)

– набор управляющих параметров. Для рассматриваемой в работе многослойной дифракционной решетки набор управляющих параметров составляют факторы заполнения {f k } , которые оптимизируются таким образом, чтобы решетка обладала максимально близкой к 100% дифракционной эффективностью в n -ом дифракционном порядке (в спектре отражения для отражающей решетки или пропускания для пропускающей) в некотором заданном диапазоне длин волн.

В общем виде целевой функционал представляет собой интегральную характеристику дифракционной решетки в отношении квадратичного отклонения дифракционной эффективности в заданном диапазоне длин волн от желаемого значения (100%) и зависит от управляющих параметров решетки. В численных расчетах интеграл заменяется суммой по некоторому набору дискретных длин волн λ _l , при этом функционал имеет следующий вид

L

F(f ) = Ef¹ - DE n (f^ ) ) 2 -                        (2)

l =1

где DE _n (f, X l ) - дифракционная эффективность многослойной решетки в n -м порядке в спектре отражения или пропускания на некоторой длине волны λ _l .

Минимизация функционала осуществляется градиентными методами, и градиент вычисляется при помощи сопряженной задачи с поставленными специальным образом граничными условиями.

2.    Вычисление функциональной производной

Перейдем к непосредственно обсуждению метода вычисления градиента и постановки прямой и сопряженной задач. В общем случае идея заключается в следующем

[3]. Функция U и параметр f связаны операторным уравнением

R( u ,f ) = 0 ,

которое предполагается разрешимым относительно U при заданном f и является обыкновенным дифференциальным уравнением с граничными условиями.

Формулу для вариации 5F функционала F(f ) = Ф( и , f ) можно представить через вариации δf и δ U

^F = ^f = Фи ^ U + Ф f f

∂f

Затем слагаемое Фи ^ и заменяется на функционал от 5f при помощи уравнения в вариациях

Ru 5 U + R f df = 0

и тождества Лагранжа

( Ф ,Я иШ) = ( R U Ф,Ш ) . (6)

Далее, функция Ф подбирается как решение уравнения R U Ф = - Фи, а из уравнения в вариациях (5) выражается R u 5 U = -R f bf , что приводит к следующей цепочке равенств

Фи ^ и = - ( R U Ф , 5 U ) = - ( Ф , R u J U ) = ( Ф , R f 5f ) = ( R f Ф , 5f ) .

Таким образом, из выражения для вариации функционала (4) получаем общую формулу для функциональной производной (или градиента)

∂F f = фf + Rf *.

Рассмотрим применение общей схемы непосредственно к нашей задаче и начнем с получения конкретного вида операторного уравнения.

2.1. Постановка прямой задачи дифракции плоской волны на дифракционной решетке

Для определенности рассмотрим волны с ТЕ-поляризацией. В этом случае уравнение Гельмгольца для y -компоненты электрического поля

д2 Ey d2 Ey , 2 .    . _

⁺ 77V ⁺ k² Ф’ z ^{) E} y = ⁰

dx2    dz2

с ограничивающими расчетную область по оси z парциальными условиями излучения в интегральной форме

d

.1 № -Ч

d

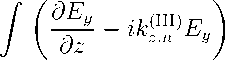
Y _n ( x ) dx = 0 ,

Z = Z s

Y n (x)dx = 2ik® 0 $ n, 0 , z =0

и условиями непрерывности тангенциальных компонент поля E _y (условия сопряжения) на границах ү _т между слоями с номерами m и m +1 решетки

I E И ү т =« ,

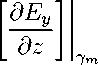
m = 0 , 1 , 2 ,..., M,

при помощи применения неполного метода Галеркина [5] сводится к матричновекторному обыкновенному дифференциальному уравнению второго порядка с граничными условиями третьего рода следующим образом. Приближенное решение E N ( x, z ) уравнения Гельмгольца ищется в виде конечного разложения по первым N функциям базиса Y n (x) = ү/^ е^{г к х,пХ} , соответствующим дифракционному порядку с номером n = 0 , ± 1 , ± 2 ,...

E N ^{( x,z )}= ^{Y ( x ) U ( z )} , ⁽¹³⁾

где Y ( x ) = (Y i ( x ) , Y ₂ ( x ) ,..., Y N ( x )) — вектор-строка первых N функций базиса, U ( z ) = ( U ₁ ( z ) ,U ₀ (z),...,U _N ( z ) } T — вектор-столбец коэффициентов разложения, зависящих от переменной z .

Таким образом прямая задача для вектора коэффициентов U (z) имеет вид

U ‘‘ ( z )+ £ (zf ) U ( z ) = 0 ,

U ‘ (0) + і Г ⁽⁰⁾ U (0) = 2 і Г ⁽⁰⁾ A o ,                            (14)

U’(zs) - іГ(м+1)U(zs) =0, где матрица

d

< ^{( z,}f ) = k0 /

Y ‘ ( x ) x ( x,z ) Y ( x ) dx - M ⁰ .

Здесь M – диагональная матрица, на главной диагонали которой расположены постоянные распространения k _xn . Матрицы Г ^{(0 ,м +1)} представляют собой диагональные матрицы, на главных диагоналях которых расположены постоянные распространения k ZInI¹ ) дифракционных порядков во внешней среде и в подложке соответственно и A _o = (1 , 0 , 0 ,..., 0) ^T — амплитудный вектор падающий на решетку волны со стороны внешней среды.

Решение полученной задачи (14) в m -м слое формально можно выписать аналитически

U m ( z ) = Q m e i ^{r m ( z} z ^{m - 1 )} A m ( z m - 1 ) + Q m e ^{І Г т (} z z ^{m - 1 )} B m ( z m - i ) , (16)

где Q _m — матрица собственных векторов, а r m - диагональная матрица собственных значений матрицы £ ( z, f ) в m -м слое, A m - амплитудные векторы облучающих структуру волн, B _m – амплитудные векторы волн, рассеянных структурой.

Численно задача (14) решается методом матриц переноса, применение которого подробно описано в работе [5]. В силу постоянства коэффициентов уравнения внутри слоя толщины h m для всей многослойной структуры, состоящей из M слоев с толщинами h i , h ₀ ,..., һ м , матрица переноса P получается перемножением матриц переноса для каждого слоя

./0

P = P h M P h M

1 ... P h i = П^Р һ т , где P h m = ^exp |i^ ₀J h m^ ,     ⁽¹⁷⁾

I - единичная матрица размерности N х N , и связывает векторы U ( z ) и V ( z ) =

— i U ’ ( z ) на границах структуры z = 0 и z = z s

(U( z . Л   pfU (0^

V ( z s)J = Pl^ oJ ■                         ⁽¹⁸⁾

При этом граничные условия имеют следующий вид:

V (0) + r ⁽⁰⁾ U (0)=2 r ⁽⁰⁾ A o ,                          ₍₁₉₎

V ( z s ) — Г ^{( м +1)} U ( z s )=0 .

Таким образом, уравнение (18) с граничными условиями (19) составляют систему линейных алгебраических уравнений для векторов U ( z ) и V ( z ) на границах многослойной структуры. Отметим, что эта система справедлива как для спектра отражения, так и для спектра пропускания, и ее решение может быть получено аналитически.

Вычислим аналитически элементы матрицы £ ( z, f ). Поскольку в однородных слоях величина диэлектрической проницаемости e ( x, z ) постоянна, матрица £ ( z, f ) имеет диагональный вид

£ (z,f ) = k | e ( x,z ) I — M ² , (20)

где I – единичная матрица. В слое с решеткой распределение диэлектрической проницаемости e ( x, z ) является кусочно-постоянной функцией, которая зависит от фактора заполнения f (который является параметром управления) и имеет следующий вид:

e ( x, z ) =

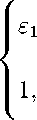
k — 1      k — 1

x e d2d_p,d2d_p + dkfk

_p =0     p =0

k—1                k x e £dp + dkfk,\d

-P =0              p =0

причем k = 1 , K , p = 0,k и « нулевой » подпериод равен d 0 = 0. Подставляя e ( x, z ) в

K интеграл и проводя интегрирование по периоду решетки, равному d =   dk, получим k=1

(^{£ ( z} , ^f )) П 1 П 2

/                                k- 1

K Cq ^ dn n1 = n2, (22)

n 1 = n 2 ,

— 2 E e p =0 p [ ( ^1 — 1) e C 0 ^f k d k — ^1 + e C o d k 1 - ( M 2 )     ,

A ² ( n i — П 2 ) _k= 1           ^{L                      1 J   v} 'ni n ²

• 1    /2п\ ² K

• 2.2.    Вариация функционала

. d (v E dk [|E1 — 1)fk' + 11 — (M )-”2 ’ где обозначено C0 = i—(n1 d

— n 2 ).

Далее задачу (14) будем рассматривать в качестве операторного уравнения.

Перейдем к рассмотрению введенного ранее целевого функционала (2)

L

F(f ) = Ф(и , f ) = E ( 1 — DEM A l ) ) ² ,                  (23)

l =1

где DE _n (f, X i ) - дифракционная эффективность многослойной решетки в n -ом порядке в спектре отражения или пропускания на некоторой длине волны λ _l . Вводя векторы В о — амплитудный вектор отраженной решеткой волны и A M ₊ i - амплитудный вектор волны, прошедшей в подложку, запишем явное выражение для дифракционной эффективности в спектре отражения

k(I)

DE r,n (f,X i ) = -f. | Bo ,n | ² , k z Oo

и в спектре пропускания

k ( Iⁿ⁾

DEt,n(f,Xi) = -Z^ |Am+i,n|2 .

^- z, o

Для вычисления вариации функционала амплитудный коэффициент отраженной волны B o ,_n в n -ом порядке удобно записать как

Bo,n = аВо, где а = (0 • • • 1 • • • 0) - вектор-строка, который состоит из нулевых элементов и единицы, находящейся на n-ой позиции. Тогда квадрат модуля равен

|Bo,n|2 = B0,nBo,n = ВО «n Во, где

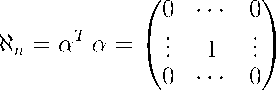
– матрица, у которой единица стоит на пересечении n -ой строки и n -го столбца. Аналогично для амплитудного коэффициента прошедшей волны A M ₊₁ ,_п в n -ом порядке

|Am+i,n|2 = AM+1 «n Am+1.

Получим вариацию функционала в виде (4)

L

5F = -2 ^[1 - DEn(f, Xi)] [6(DEn)u + 5(DEn)f].

i =i

Поскольку DE _n (f, X l ) явно от f не зависит, то 5(DE _n ) f = 0. Учитывая условия связи амплитудных векторов падающей, прошедшей и отраженной волн

Ao + Bo = U(0),    Am+i = U(zs), вычислим вариацию 3(DEn)u. Рассмотрим сначала случай спектра отражения

6(DE rn )и = 5

(kw B o « n B o')   =

-z,o             U к (I) /

= -^ ^U * (0) « n ( U (0)

^- z, o

- A o ) + ( U (0) - A o ) ’ « n 5 U (0)) .

k zIn

Для удобства дальнейших вычислений обозначим X (0) = -щ- N _n (U (0) — Aq) . Тогда выражение для 5(DE n ) U примет вид

5 ( DE r,n )u = [X * (0) 5 U (0)] * + X * (0) 5 U (0) .                   (33)

Аналогично для случая спектра пропускания

5 ( DE t,n )u = 5

(

^{( III )}

z,n kz,0

∗

A M +1

^R n A M +1^

U

k ( Iⁿ⁾

= -z,^ (5U*(zs) N U(zs) + U*(zs) Rn 5U(zs)) = kZ,0

= [ Z * ( z s ) 5 U ( z s ) ] * + Z * ( z s ) 5 U ( z s ) ,

_{k z} ( I _n II )

где обозначено Z ( z _s ) = —jjy N _n U ( z _s ).

k Z, 0

И, таким образом, окончательно получаем формулы для вариация функционала в случае спектра отражения

5F = — 2 ^2 [ 1 — DE r,n ( f, A i ) ] [( X * (0) 5 U (0) ) * + X * (0) 5 U (0) ]          (35)

1 =1

и в случае спектра пропускания

5F = — 2 52 [ 1 — DE t,n (f, A i ) ] [( Z * ( z s ) 5 U ( z s ) ) * + Z * ( z s ) 5 U ( z s ) ] .         (36)

l =1

• 2.3.    Задача в вариациях

Операторное уравнение для (14) в виде (3)

R ( U ,f ):    U ‘‘ ( z )+ C ( z,f ) U ( z ) = 0 ,

U ‘ (0) + і Г ⁽⁰⁾ U (0) = 2 і Г ⁽⁰⁾ A o ,                      (37)

U ’ ( z s ) — І Г ^{( М +1)} U ( z s ) = 0 .

Для того, чтобы получить уравнение в вариациях в форме (5), проварьируем R ( U , f )

5R ( U , f ) = Ru 5 U + R f 5f =

= 5U‘‘(z) + C(z, f )5U(z) + Cf (z, f )U(z)5f = 0, где RU5U = 5U’’(z) + C(z, f )5U(z) и Rf 5f = Cf (z, f )U(z)5f. Выполним варьирование граничных условий (14). На левой границе

( U + 5 U ) ‘ (0) + і Г ⁽⁰⁾ ( U + 5 U )(0) = 2 i r ^(o) A o , U ‘ (0) + 5 U ‘ (0) + і Г ⁽⁰⁾ U (0) + і Г ⁽⁰⁾ 5 U (0) = 2 i r ^(o) A o .

С учетом (14) приходим к следующему граничному условию в нуле для 5 U (0)

5U‘(0) + іГ(0) 5U(0) = 0.

Аналогично на правой границе

5U‘(zs) - ІГ(М+1)6U(zs) = 0.

Итак, в ходе проделанных выше преобразований получена задача в вариациях

5 U" ( z ) + ( (z, f )3 U (z) + ( f (z, f ) U ( z ) f = 0 ,

5U‘(0) + іГ(0) 5U(0) = 0,

3U'(zs) - І Г ^{( М +1)} 5 U ( z s ) = 0 .

• 2.4.    Постановка сопряженной задачи

Чтобы получить сопряженное уравнение для функции ^ ( z ), воспользуемся тождеством Лагранжа (6) и выполним интегрирование по частям с учетом граничных условий (42) для 5 U ( z )

(Ф, Ru5U) = J Ф'(;) (iU(z) + ((z, f )SU(z)) dz = zs

= I ( Ф *’’ (z) + Ф * ( z ) ( (z, f ))5U(z)dz - [ Ф *‘ ( z s ) - Ф * ( z s ) i Г ^{( M +1)} ] 5 UU )+

+ [ Ф *‘ (0) + Ф * (0) і Г ^(о) ] 5 U (0) = №Ф , 5 U ) , (43)

где под операцией ^∗ понимается комплексное сопряжение и транспонирование.

Здесь и далее функция Ф * ( z ) представляет собой вектор-строку комплексно сопряженных к функции U ( z ) коэффициентов разложения. Будем выбирать ее так, чтобы

Ф *‘‘ ( z ) + Ф * ( z ) ( ( z,f ) = 0 .                               (44)

Это уравнение является общим для двух спектров. Однако граничные условия для спектра отражения будут несколько отличаться от граничных условий для спектра пропускания. Рассмотрим каждый спектр отдельно.

• 2.4.1.    Спектр отражения

Используя явное выражение для вариации функционала в случае спектра отражения (35), на левой границе при z = 0 положим

[Ф*‘(0) + Ф* (0)ir(0)]5U(0) = -X* (0)5U(0), а на правой при z = zs

-[Ф*‘(zs) - Ф*(zs)iГ(M+1)]5UU) = 0.

Тогда для функции Ф * ( z ) имеем следующую постановку сопряженной задачи для случая спектра отражения

Ф *‘‘ ( z ) + Ф * ( z ) ( ( z,f ) = 0 ,

Ф*‘(0) + Ф* (0)іГ(о) = -X* (0),

Ф *‘ ( z _s ) - Ф * ( z _s ) і Г ^{( м +1)} = 0 .

Однако полученную сопряженную задачу удобнее переписать для случая, когда функция Ф ( z ) — вектор-столбец и ( Г ) * - комплексно сопряженная матрица. Для этого применим к операцию комплексного сопряжения и транспонирования

Ф ’’ ( z )+ е * (z,f ) Ф ( z ) = o ,

Ф ‘ (0) - i ( Г ⁽⁰⁾ ) * Ф (0) = - X (0) ,                           (48)

Ф ‘ ( z s )+ i ( Г ^{( м +1)} ) * Ф ( z s ) =0 .

Таким образом, задача (48) является сопряженной к задаче (14) в случае спектра отражения.

• 2.4.2.    Спектр пропускания

В случае спектра пропускания на левой границе при z = 0 положим

[Ф*’ (0) + Ф*(0)іГ(0) ]5U(0) = 0, а на правой границе, при z = zs, с учетом формулы для вариации функционала в случае спектра пропускания (36)

-[Ф*‘(zs) - Ф*(zs)іГ(м+1)]5U(zs) = -Z(zs).

Тогда для вектора-строки Ф * ( z ) имеем

Ф *‘‘ ( z ) + Ф * ( z ) е (zf ) = 0 ,

Ф*’ (0) + Ф*(0)іГ(0) =0,

- Ф *’ ( z s ) + Ф * ( z _s ) І Г ^{( М +1)} = - Z * ( z s ) .

и, также применяя операцию комплексного сопряжения и транспонирования, перейдем к сопряженной задачи для вектора-столбца Ф ( z )

Ф ’’ ( z )+ е * ( z,f ) Ф ( z ) = o ,

Ф ‘ (0) - І ( Г ⁽⁰⁾ ) * Ф (0) = 0 ,                                    (52)

- Ф ‘ ( z s ) - i ( Г ^{( м +1)} ) * Ф ( z s ) = - Z ( z s ) .

Задача (48) представляет собой сопряженную к (14) задачу в случае спектра отражения.

Решение сопряженных задач (48) и (52) в m -м слое будет аналогично решению (16) прямой задачи

Ф m ( z ) = Q m e ^{i r m ( z-Z} m^{- 1 )} C m ( z m -₁ ) + Q m e ^{-i r} m ^{( z-Z m - 1 )} D m ( z m — 1 ) .          (53)

Здесь Q ^∗ _m и ( Г т ) ² - матрицы собственных векторов и собственных значений матрицы е * ( z, f ) в m -м слое соответственно, причем матрица ( Г т ) ² - диагональная, а векторы C 0 и D 0 соответствуют векторам A 0 и B 0 .

• 2.5.    Формула для градиента

С учетом предположений, сделанных в предыдущем разделе, интеграл (43) в случае спектра отражения сводится к следующему виду

( Ф , Ru5U ) = - X * (0) 5 U (0) = ( R U Ф , 5 U ) .                  (54)

Выражая из (38) R f bf и применяя тождество Лагранжа, преобразуем X * (0) J U (0)

-X* (0)bU(0) = (RU Ф, JU) = (Ф, RubU) = -(Ф, Rf bf) = -(Rf Ф, bf).

То же проделаем и для [ X * (0) b U (0)] *

-[X*(0)bU(0)]* = (RU Ф, bU)* = (Ф, RubU)* = -(Ф, Rfbf )* = -(Rf Ф, bf )*.

Подставляя эти преобразованные величины в (35), находим выражение для вариации функционала с случае спектра отражения в операторном виде

L bF = -2 £ [1 - DEr,n(f, Xi)] [(RfФ, bf )* + (RfФ, bf)] , i=i из которого легко получается формула для градиента в случае спектра отражения

∂F ∂f

- 2 ]T [1 - DE r,n ( f, X i )] [ ( R f Ф ) * + R f Ф ] = = - 4 = E L =i [1 - DE rM X i )] Re ( R f Ф ) .

С учетом преобразований

Z * ( z s ) = ( R f Ф ) *

Z(zs) = Rf Ф, в случае спектра пропускания получаются аналогичные выражения для вариации функционала

L bF = -2£[1 - DEt,n(f, Xi)] [(RfФ, bf )* + (RfФ, bf)]             (60)

i=i и для градиента

∂F ∂f

L

- 4^[1 - DE t,n (f,X i)] Re(R f Ф ) . i =i

Перейдем от операторного представления к интегральному. Воспользовавшись тождеством Лагранжа (6) и выражением (38), определим интеграл R _f ^∗ Ψ

R f Ф =

z s

I Ф * ( z ) e f ( z,f ) U ( z ) dz, 0

где элементы матрицы ^ f (z, f ) вычисляются аналитически (см. формулу (73)), и получим выражение для функциональной производной в интегральном виде

∂F ∂f

L

^{- 4} ^ ^{[1 - DE} n ^{( f}, ^X i ^{)] Re} i =i

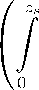
Ф * «f ( z,f ) U ( z ) dz

Формула (63) справедлива как для спектра отражения, так и для спектра пропускания, где DE n (f, X f ) - дифракционная эффективность в n -м порядке спектра отражения или пропускания. Здесь U ( z ) и Ф * ( z ) - решения прямой и сопряженной задач, получаемые при помощи метода матриц переноса.

3.    Численная реализация решения сопряженной задачи и вычисления градиента

Алгоритм решения прямой задачи дифракции плоской волны на дифракционной решетки методом матриц переноса подробно изложен в работе [5]. В данном разделе кратко рассмотрим применение метода матриц переноса для решения сопряженной задачи.

Интеграл в (63) вычисляется по формуле численного интегрирования прямоугольниками, для чего слой с решеткой разбивается на M _h подслоев, причем матрица £ ( z, f ) одинаковая для каждого подслоя.

• 3.1.    Метод матриц переноса для решения сопряженной задачи

Матрицы переноса для каждого слоя и для всей структуры в случае сопряженной задачи имеет вид, аналогичный соответствующим матрицам в случае прямой задачи (17). То есть,

( ША p /WA W ( z s )J = 4.W (G^ ’

где матрица P , связывающая вектора Ф ( z ) и W ( z ) = — i Ф ‘ ( z ) на границах многослойной структуры, представляется через матрицы переноса слоя

M

P = П P h m ■

P h m = exp {i(° 0) h m} •

Для случая спектра отражения уравнение (64) с граничными условиями

W (0) - ( Г ⁽⁰⁾ ) * Ф (0) = i X (0) ,

W(zs) + (Г(м+1))* Ф(zs) = 0, представляют собой систему сопряженных к системе (18)–(19) линейных алгебраических уравнений для векторов Ф(z) и W(z), решение которой так же можно получить аналитически.

Аналогично в случае спектра пропускания уравнение (64) и граничные условия

W (0) - ( Г ⁽⁰⁾ ) * Ф (0) = 0 ,

W(zs) + (Г(м+1))* Ф^) = -iZ(zs), являются системой сопряженных к системе (18)–(19) линейных алгебраических уравнений для векторов Ф(z) и W(z), решение которой можно получить аналитически.

• 3.2.    Вычисление градиента

Будем вычислять интеграл в (63) по численной формуле прямоугольников. Поскольку в однородных слоях матрица £ f ( z, f ) = 0, будем вести расчеты на отрезке [0 , h i ], где h i - толщина 1-го слоя с решеткой. Разобьем отрезок [0 , h i ] на M _h 1 равных частей A h 1 = , ,¹ . Решение прямой и сопряженной задач в ^ -й части разбиения A h _i

M h 1

решетки можно представить через матрицы P ^ (A h 1 ) и P „ (A h _i ) соответственно

! i A ! ,_д , /ШЛ     / *, (^A h i ) \ p„_д/.) fWA , .

VlA hjJ = ^{P (A h i} ) ^(QV ’     ^„(A h i J = ^{P (A h i )} ^Ф(0)) ’     ⁽⁶⁸⁾

где ^ = 1,Mh1. Поскольку значения функций при z = 0 известны из граничных условий, то при z = АҺ1 для вектора и^(АҺ1) получим следующее выражение иДАЛ,) = PJ1(Ah1)U(0) + Р^АҺ, )V(0).

Аналогично для вектора Ф _м (А Һ 1 )

Ф _М (А Л 1 ) = P ^ i (А Һ 1 ) Ф (0) - Р^А Һ , ) W (0) .                 (70)

Здесь матрицы Р ^ (А Һ 1 ) и Р ^ (А Һ 1 ) в слоях решетки вычисляются аналогично P -матрице всей структуры (17).

Тогда, учитывая полученные выражения, интеграл в (63) можно вычислить по формуле численного интегрирования прямоугольниками h1                                   Mh1

/ Ф *^ )^( z,f ) U ( z ) dz =А Һ 1 £ф; (А Л1 Xf (h i ,f ) и „ (А Һ і ) .

₀                                  µ =1

Таким образом, численная формула для градиента имеет вид

∂F ∂f

L

—4 ^ [1 — DEn (f, ^l)] Re l=1

M h 1

А Һ 1 £ ФД А Һ 1 Xf ( h i ,f М(А Һ 1 )

µ =1

Матрица ( Һ 1 , f ) для k -го подпериода решетки является трехмерной, ее элементы одинаковы для каждого слоя А Һ 1 разбиения решетки и вычисляется аналитически один раз сразу для всей решетки по следующей формуле:

(«f (z.f )) А

(?) (?)

d k

7<^{£ 1}

d k

7<£

C 0

1) e

1) ,

(

k- 1

Е dp+dk fk p=0

)

ni = П2, n1 = n2,

где при к = 0 « нулевой » подпериод равен d o = 0, и обозначено C o = i— (n 1 — п ₂ ). d

4.    Результаты вычислительного эксперимента

Предложенный в данной работе градиентный метод решения задач оптимального управления был реализован в виде программного кода на базе пакета программ Matlab . С помощью реализованного алгоритма решены задачи синтеза отражающей и пропускающей дифракционных решеток, параметры которых были взяты из работ [6] и [7] соответственно. Рассматривались задачи синтеза решеток с прямоугольным профилем, определяемым одним и десятью параметрами управления. Для проверки и отладки работы алгоритма градиент, вычисленный по формуле (72), сравнивался с градиентом, вычисленным конечно-разностным методом. Во всех расчетах удерживалось N = 9 дифракционных порядков, при интегрировании слой с решеткой разбивался на M h = 15 равных частей.

• 4.1.    Отражающая решетка

Синтезируется многослойная дифракционная решетка для использования в качестве зеркала внешнего резонатора полупроводникового лазера, обеспечивающая стабилизацию длины волны излучения и подстройку лазера в диапазоне длин волн от 485 до 515 нм (зелено-голубая область видимого спектра) [6]. Такая решетка должна обладать максимальной дифракционной эффективностью в конфигурации Литтроу в минус первом порядке в заданном диапазоне длин волн в спектре отражения.

Структура синтезируемой решетки представлена на рис. 2. В качестве однородной многослойной структуры выбрано 20-слойное четвертьволновое зеркало, с показателями преломления материалов слоев n _H = 2 , 375 - оксид ниобия(V) (Nb ₂ O ₅ ) и U l = 1 , 46 - кварц (SiO ₂ ), настроенное на длину волны А = 500 нм, то есть на центральною длину волны заданного диапазона. Решетка выполняется из кварца, а подложка - из оксида ниобия с показателями преломления n gr = 1 , 46 и Пш = 2 , 375 соответственно.

x

z

d

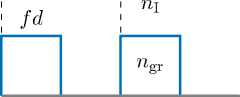
nH nL nIII

Рис. 2 . Синтезируемая многослойная отражающая дифракционная решетка, определяемая одним параметром управления f . Параметры профиля решетки: d = 384 , 8 нм - период решетки, h = 438 , 6 нм - глубина профиля, Һ 0 = 21 , 1 нм -толщина дополнительного однородного слоя из материала решетки

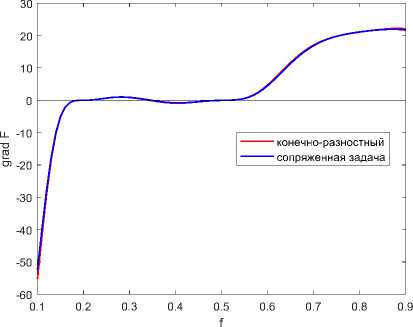
На первом этапе для того, чтобы убедиться в правильности полученных выражений, вычисленный при помощи сопряженной задачи градиент (72) сравнивается с градиентом, полученным конечно-разностным методом. Как видно на графике зависимости градиента от управляющего параметра, показном на рис. 3б, вычисленные разными методами значения градиента совпадают в пределах допустимой погрешности.

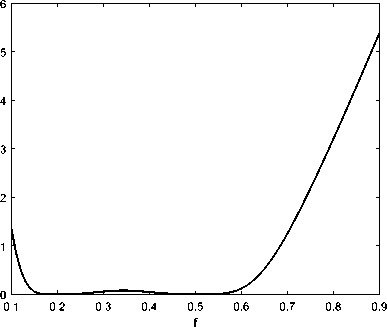
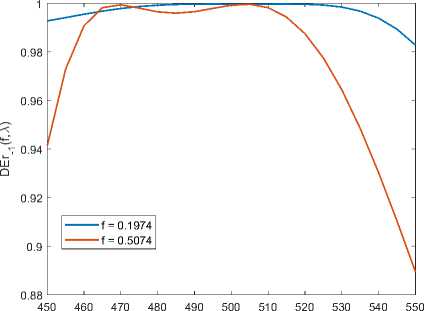
В ходе вычислений были получены два оптимальных значения фактора заполнения: при начальном приближении f ₀ = 0 , 3 оптимальный фактор заполнения равен f = 0 , 1974, а при f ₀ = 0 , 6 - f = 0 , 5074. Объяснение этому можно найти, обратившись к графику зависимости функционала от фактора заполнения (см. рис. 3а), на котором видны две точки минимума. В зависимости от выбора начального приближения по направлению антиградиента можно ≪ прийти ≫ в тот или иной минимум. И, как показано на рис. 4, эти две точки действительно являются оптимальным решением, поскольку значения дифракционной эффективности для них близки к единице, что и требовалось в постановке задачи.

Функционал                                                 Градиент функционала

а) б)

Рис. 3 . а) Зависимость функционала от фактора заполнения; б) Зависимость градиента, вычисленного по формуле (72) и конечно-разностным методом, от фактора заполнения

Дифракционная эффективность

А , нм

Рис. 4 . Зависимость дифракционной эффективности в - 1-м порядке от длины волны

• 4.2.    Пропускающая решетка

Перейдем к рассмотрению задачи оптимизации бинарной пропускающей решетки с большим числом параметров, представленной в работе [7]. Данная решетка проектируется из фторида бария (BaF 2 ) с показателем преломления n gr = 1 , 396, чтобы заменить треугольную решетку, обеспечивающую пропускание энергии нормально падающего излучения с длиной волны А = 10 600 нм в первый дифракционный порядок с максимальной эффективностью. Для этого каждый период прямоугольной решетки, с d = 40 955 , 3 нм и h = 24 646 , 9 нм, разбивается на 10 равных частей, каждой из которых соответствует свой фактор заполнения (см. рис. 5). Такие решетки могут быть использованы в качестве оптического ограничителя для предотвращения повреждения работающих в ИК-диапазоне элементов наведения управляемых ракет ослепляющим лазерным оружием.

В ходе решения задачи оптимизации методом были найдены оптимальные значения факторов заполнения, представленные в таблице, при которых дифракционная эффективность в первом порядке составляет 90,34%.

f 1         f 2          ^{· · ·}        f 10

Рис. 5 . Схематическое изображение замены треугольной пропускающей решетки на бинарную пропускающую решетку

Таблица

Оптимальные значения факторов заполнения

f 1	f 2	f 3	f 4	f 5	f 6	f 7	f 8	f 9	f 10
0	0	0,0136	0,1537	0,2470	0,3186	0,3988	0,4492	0,5457	1

Кроме того, время работы минимизирующего алгоритма с градиентом, вычисляемым при помощи решения сопряженной задачи, оказывается в 5 меньше, чем время работы аналогичного алгоритма с вычислением градиента конечно-разностным методом. Это связано с тем, что на каждой итерации в первом случае целевой функционал вычисляется 2 раза (решение прямой и сопряженной задач), в то время как во втором случае – 11 раз (решение прямой задачи 1 раз для вычисления функционала и 10 раз для вычисления градиента).

Заключение

В работе представлена методика вычисления градиента целевого функционала для применения к решению задачи синтеза одномерных многослойных отражающих и пропускающих дифракционных решеток. Кроме того, приведена строгая математическая постановка задачи оптимизации и полная формулировка численного алгоритма ее решения. Результаты численных экспериментов показывают надежность градиентного метода и его устойчивость относительно увеличения количества параметров управления. Это позволяет в дальнейшем перейти к рассмотрению общей постановки задачи синтеза, при которой профиль решетки определяется произвольной функцией без каких-либо специальных априорных предположений (кроме практической реализуемости), являющейся результатом непосредственного решения задачи.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 23-11-00056).