Об исследовании интегрально-суммарных контрольных карт

Для проведения процедуры анализа рассеивания значений в показателях качества продукции широкое применение находят методы контрольных карт, графически отражающих изменения показателей качества, предусматривающие применение экономичных статистических оценок и разделяющие зоны неизбежного и устранимого рассеиваний. Применение контрольных карт основывается на основных принципиальных положениях: все процессы с течением времени отклоняются от заданных характеристик; незначительные отклонения отдельных значений измеряемых показателей являются непрогнозируемыми; стабильный процесс изменяется случайным образом, но таким образом, что группы значений измеряемых показателей имеют тенденцию находиться в прогнозируемых границах; нестабильный процесс отклоняется с силу неслучайных факторов.

Известно, что все эти методы делятся на две большие группы: простые контрольные карты и специализированные (в том числе интегрально-суммарные). Первая группа классифицируются также на две подгруппы, причем критерием классификации служит контролируемый признак. Одна подгруппа методов предназначена для контроля параметров качества, представляющих собой непрерывные случайные величины, значения которых являются количественными данными параметра качества. Вторая – для контроля параметров качества, представляющих собой дискретные случайные величины, значения которых являются качественными данными. В рамках этих подгрупп методы классифицируются в соответствии с назначением (для контроля положения центра рассеяния, разброса данных, доли бракованной продукции и т.п.). Также возможна классификация по критерию постоянного и вариативного объемов выборки.

Таким образом, разнообразие контрольных карт вызывает существенные затруднения для пользователей при выборе конкретной для целей управления технологическими процессами, тем более что на практике обычно сведения о свойствах экспериментальных данных довольно ограниченны. Вместе с тем свойства алгоритмов обработки результатов измерительной информации наряду со свойствами исходных данных оказывают существенное влияние на качество принимаемого решения, а оценивание соответствующих составляющих может стать сложной и трудоемкой задачей, требующей значительной априорной информации.

Все это обусловливает необходимость целенаправленного исследования контрольных карт, а по существу алгоритмов обработки измерительной информации в рамках статистического управления технологическими процессами.

Были рассмотрены контрольные карты, относящиеся к группе интегрально-суммарных (или «с памятью»), такие как контрольная карта экспоненциально взвешенного скользящего среднего (EWMA ‒ exponentially weighted moving averages), предназначенная для оценки изменчивости процесса по экспоненциально сглаженным скользящим средним арифметическим значениям, и контрольная карта скользящего среднего (MA ‒ moving average control chart) – предназначена для оценки состояния процесса по средним арифметическим последних n наблюдений. Интерпретация данных карт имеет много общего, т.е. карты данного типа имеют контрольные границы, в отличие от карт кумулятивных сумм, для интерпретации которых чаще всего используется «маска».

Интегрально-суммарные контрольные карты могут применяться при контроле по количественным и альтернативным признакам. В соответствии со своим названием они агрегируют данные, накапливаемые от одной выборки к другой, а не рассматривают каждую выборку (группу) изолированно. По этой причине они имеют преимущества над более традиционными контрольными картами Шухарта, так как обеспечивают возможность обнаружения небольших изменений среднего значения процесса и в то же время дают более ясное указание на то, где произошли эти изменения.

Применительно к задачам управления технологическими процессами наибольший интерес представляют свойства контрольных карт, непосредственно влияющие на точность полученных результатов, такие как стандартная и дополнительная неопределенности, средние длины серий при налаженном и разлаженном процессах.

Однако для эффективного использования контрольных карт на практике существенны и другие свойства, например, показатели чувствительности, характеризующие изменение значений параметров распределения результатов контроля от изменения параметров моделей исходных данных, характеризующих различные условия применения контрольных карт. Причем эти свойства тесно связаны с точностными характеристиками исследуемых методов.

Поэтому целью данной работы было исследование свойств контрольных карт с памятью, в частности чувствительность к проявлению в первичных данных контроля отдельных сигнальных признаков. Моделью для сравнения выбраны хорошо изученные карты Шухарта, для интерпретации которых также используется правило «8 сигнальных признаков», появление которых на карте свидетельствует о разладке процесса.

Формирование набора типовых моделей исходных данных основывалось на методах имитационного и математического моделирования с использованием знаний, опыта и интуиции при оценке влияния различных факторов на параметры технологического процесса. Моделирование состояло в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами и позволило построить модели исходных данных (массивы результатов контроля), описывающие технологические процессы так, как они проходили бы в действительности.

Типовые модели исходных данных, которые по существу являются массивами результатов текущего контроля, представляют собой совокупность трех элементов: модель полезных сигналов; модель, отражающая план (размещение) измерений; модель погрешностей исходных данных.

В качестве модели полезных сигналов принят массив данных, значения которых отражают разладку технологического процесса во времени, т.е. изменение контролируемого параметра при воздействии на него комплекса технологических факторов. Причем характер разладки в каждой типовой модели соответствует правилу «8 сигнальных признаков». Модели размещения измерений конкретизируют план измерительного эксперимента, задавая точки выполнения наблюдений и число наблюдений в каждой точке. Наличие модели погрешностей объясняется тем, что в реальности на технологический процесс действуют ряд неучтенных факторов, что отражается на распределении значений контролируемого параметра.

Таким образом, для проведения исследования нами был сформирован набор типовых моделей исходных данных, распределенных нормально и имеющих различные объемы. Кроме того, массивы данных имели элементы «искусственной» разладки, т.е. были сформированы таким образом, чтобы в значениях основных статистических характеристик прослеживалось отражение следующих 8 сигнальных признаков:

• ‒    1 или более точек вышли за контрольные пределы;

• ‒    серия из 7 или более точек лежит с одной стороны от центральной линии. Сюда же относят случаи, если не менее 10 из 11 точек, или не менее 12 из 14 точек, или не менее 16 из 20 точек лежат с одной стороны от центральной линии;

• ‒    серия из 6 или более точек образует непрерывно повышающуюся (понижающуюся) кривую;

• ‒    серия из 14 или более, попеременно возрастающих и убывающих точек;

• ‒    точки образуют кривую с повторяющейся формой и примерно одинаковыми интервалами;

• ‒    2 из 3 последовательных точек лежат в крайней трети диапазона контрольных пределов;

• ‒    4 из 5 точек подряд лежат с одной стороны от центральной линии и не попадают в центральную треть диапазона контрольных пределов;

• ‒    серия из 8 точек расположена с двух сторон от центральной линии, при этом ни одна точка не попадает в центральную треть диапазона контрольных пределов.

Показателями модели погрешности в типовых моделях исходных данных были выбраны индекс потенциальной пригодности, индекс отношения пригодности и индексы нижней / верхней потенциальной пригодности процесса. Обычно эти показатели используются для оценки качества технологических процессов.

Индекс потенциальной пригодности (C p ) является наиболее простым и самым естественным показателем пригодности производственного процесса и определяется как отношение размаха допуска к размаху процесса. При использовании границ ±3 сигма данный показатель можно выразить в виде

C p = (ВГД-НГД)/(6*сигма),                     (1)

где ВГД – верхняя граница поля допуска, НГД – нижняя граница поля допуска.

Данное отношение выражает долю размаха кривой нормального распределения, попадающей в границы допуска.

Индекс отношения пригодности (C r ) является обратным к показателю C p и вычисляется как отношение 1/C p :

C r = (6*сигма) / (ВГД-НГД).                    (2)

Поскольку индексы потенциальной пригодности и отношения пригодности процесса имеют ряд недостатков, а именно данные показатели могут дать неверную информацию о производственном процессе в том случае, если среднее процесса отличается от номинального, иными словами, если процесс не центрирован. Поэтому в ряд показателей, характеризующих модель погрешности в типовых моделях исходных данных, нами были введены индексы нижней /верхней потенциальной пригодности C pi , C pu .

Нецентрированность, или смещенность, процесса производства выразили следующим образом. Сначала определили верхний и нижний показатели пригодности для отображения отклонений наблюдаемого среднего процесса от нижней и верхней границ поля допуска. Затем, приняв в качестве размаха процесса границы ±3 сигма , вычислили соответственно индексы C pl , C pu :

C pl = (Среднее ‒ НГД)/3*сигма и

C pu = (ВГД ‒ Среднее)/3*сигма. (3)

Сравнение значений верхнего и нижнего показателей пригодности показывает, насколько процесс является центрированным. Таким образом, третья составляющая (модель погрешности) типовых моделей исходных данных включает превышение размаха процесса над размахом допуска, а также нецентрированность процесса.

В данной работе представлены результаты сопоставительных исследований эффективности контрольной карты Шухарта и интегрально-суммарных карт экспоненциально взвешенного скользящего среднего (EWMA) и скользящего среднего (МА) на типовых моделях исходных данных нормально распределенных.

В качестве показателя эффективности использована средняя длина серии выборок от начала контроля до первого пересечения границы регулирования при налаженном и разлаженном технологических процессах соответственно. Известно, что под средней длиной серии налаженного процесса понимают среднее число выборок между наладками технологического процесса при неизменном значении математического ожидания контролируемого параметра, а под средней длиной серии разлаженного процесса понимают среднее число выборок, необходимое для обнаружения разладки процесса. В случае когда математическое ожидание контролируемого параметра соответствует значению для налаженного процесса, средняя длина серии определяется продолжительностью до появления ложного сигнала разладки, ведущего к излишней наладке. Когда же математическое ожидание контролируемого параметра соответствует его значению для разлаженного процесса, средняя длина серии представляет запаздывание в обнаружении разладки процесса. Поскольку область применения контрольных карт ограничивается их чувствительностью к разладке технологического процесса, основным показателем эффективности был выбран показатель, характеризующий среднюю длину серии при разлаженном процессе.

В данной работе под моментом разладки процесса был принят номер выборки, значения статистических характеристик которой отражали проявление первого «сигнального» признака. Многие исследователи рекомендовали использовать для интерпретации контрольных карт и принятия решения только первый сигнальный признак – «одна или более точек за пределами контрольных границ».

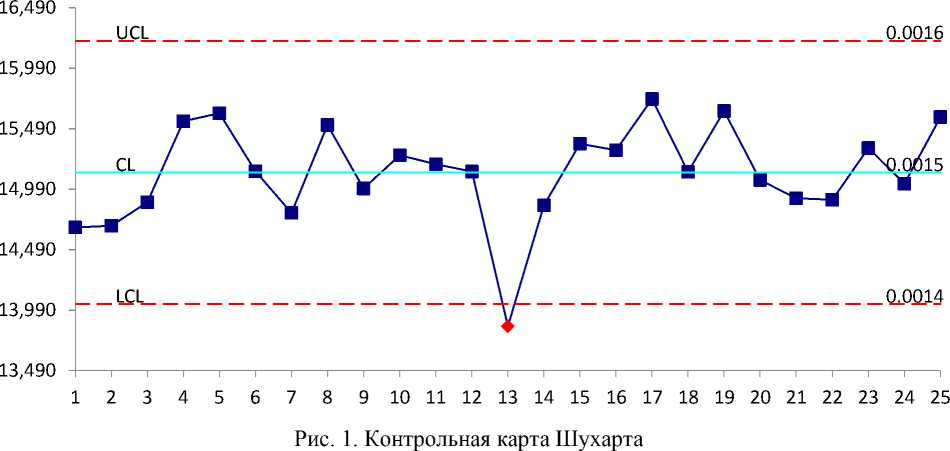
На рисунках представлены контрольные карты, построенные на моделях исходных данных (смоделированные массивы результатов контроля), содержащих первый сигнальный признак.

Как видно из рисунка 1, на котором изображена обычная контрольная карта Шухарта, на 13-й выборке было зарегистрировано проявление первого сигнального признака, т.е. выход 13-го значения за нижний контрольный предел, хотя значения последующих выборок располагаются в прогнозируемой зоне. В целом такая ситуация характеризует процесс как стабильный.

На рисунке 2 изображена интегрально-суммарная карта экспоненциального скользящего среднего EWMA. Она также построена на типовых моделях исходных данных, в которых в качестве модели полезных сигналов введена искусственная разладка в виде первого сигнального признака.

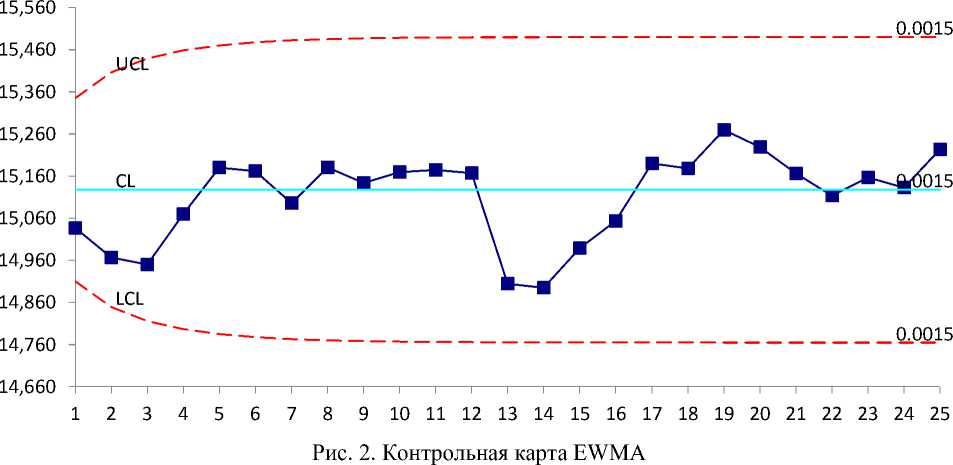
На рисунке 3 изображена карта скользящего среднего MA. На ней, так же как и на карте EWMA, расположение точек в области «искусственной» разладки характеризуется их близостью к нижнему контрольному пределу.

Таким образом, на картах EWMA и MA в зоне разладки процесса мы можем наблюдать только приближение к контрольной границе, но не выход за ее пределы, т.е. интегрально-суммарные карты не среагировали на сигнальный признак. Такая картина наблюдается, если за контрольные пределы на карте Шухарта вышла только одна точка, а значения статистики в двух соседних выборках находятся в центральной трети. Если за пределы контрольной границы на карте Шухарта вышли две последовательные точки или одна точка, но значения статистики в соседних выборках располагаются в крайних третях и приближены к значению контрольной границы, то интегрально-суммарные карты регистрируют разладку. Многократные построения всех трех карт на подобных массивах различных объемов с первым сигнальным признаком показывают устойчивые результаты.

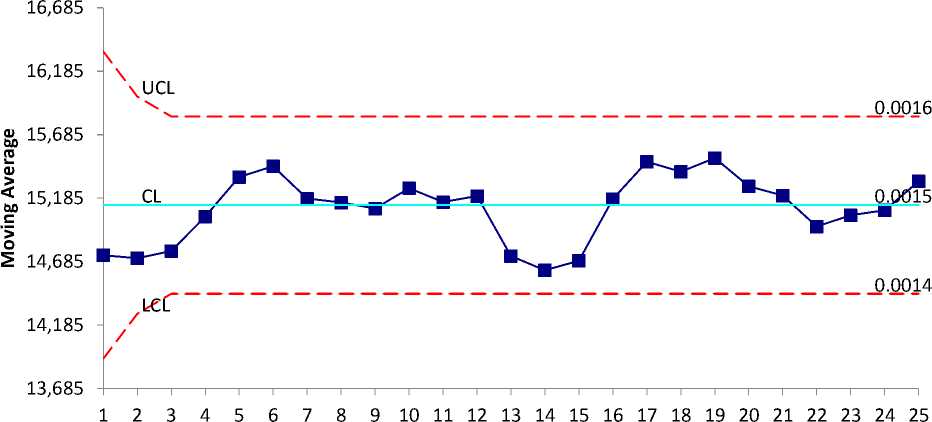
Рис. 3. Контрольная карта МА

Анализ полученных данных позволяет сделать следующее предположение: при использовании одного и того же массива для построения как простых карт, так и для интегральносуммарных, различие в методике обработки данных контроля не снижает чувствительность интегрально-суммарных карт к проявлению в первичных данных первого сигнального признака по сравнению с простыми картами, но влечет за собой снижение чувствительности к случайным выбросам, что делает их применение более ценным для снижения риска излишней наладки при управлении технологическими процессами.