Об эффективности возбуждения быстрой и медленной волн био в водо- и газонасыщенных средах

Электронный журнал «Техническая акустика»

С середины прошлого века обсуждается вопрос о возможности существования и распространения двух типов продольных акустических волн или P-волн первого и второго рода в средах, содержащих «открытые» поры. Наличие двух типов волн сжатия в среде, состоящей из скелета и флюида, предсказано ещё Я. И. Френкелем [1] и существенно развито в работах М. А. Био [2, 3]. Детальный анализ различных акустических характеристик Р-волн 1-го и 2-го рода, в том числе скорости распространения и коэффициента затухания, выполнен известными авторами В. Н. Николаевским [4], Косачев-ским Л. Я. [5] и развивается далее рядом специалистов в настоящее время. В отличие от исследований фазовой, групповой скорости распространения и коэффициента затухания указанных волн, не столь многочисленны работы по анализу эффективности возбуждения Р-волн обоих типов, а также посвящённых рассмотрению особенностей пространственной структуры этих волн при возбуждении вибраторами пространства или полупространства, образованного пористой флюидонасыщенной средой.

Такой анализ проведён только в некоторых частных случаях, например, при моделировании вибровоздействия на грунт сейсмическим вибратором, где рассчитано поле упругих колебаний, порождаемых силовым источником, установленным на поверхности полуограниченной газонасыщенной пористой среды [6, 7]. При этом теоретические расчёты касались модели рыхлых грунтов, где может наблюдаться превышение скоро- стью акустической волны в воздухе скорости волн сжатия в грунте. На такие соотношения скоростей нередко указывается в работах по экспериментальным исследованиям сейсмических параметров грунтов [8]. При решении задач волнового возбуждения в двухкомпонентных средах требуется более детальный анализ влияния смены параметров упругости и плотности флюида в порах среды на характеристики акустических волн обоих типов. Представляет также интерес получить сравнительные данные по эффективности излучения указанных волн источником типа центр пульсирующего давления в простейших условиях безграничной среды. Многочисленные натурные эксперименты [9] по регистрации сейсмического отклика в грунте на воздействие взрывных и вибрационных источников свидетельствуют о заметном различии в сигналах при расположении пункта излучения в пластах с высокой флюидонасыщенностью и в противоположном случае, когда среда характеризуется обеднённым флюидосодержанием, хотя упругие характеристики скелета и параметры проницаемости в сравниваемых ситуациях близки по значениям. Подход, предложенный Био, в принципе позволяет получить качественные представления по сформулированным вопросам. Однако ввиду отсутствия в литературе непосредственного ответа на вопрос о соотношении скоростей и о коэффициентах затухания упругих волн Р-1 и P-2 в средах, существенно различающихся по поровому заполнению, а также об эффективности их излучения источником, в настоящей работе предпринята попытка его решения на основе указанного подхода.

ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ УСЛОВИЙ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН СЖАТИЯ

В работе [3] показано, что упругая дилатация скелета e и жидкой фракции e в поле Р-волн, бегущих по двухкомпонентной флюидонасыщенной среде с открытыми порами, подчиняется системе двух волновых уравнений:

д2                        д

V ( Pe + Q e ) = — ( p„ e + p 12 E ) + bF ( к ) — ( e - e ), д t ²                             д t

V 2( Qe + Re ) = — (pn e + p 22 e ) - bF (к) - (e - e ), д t2                           д t где P, Q, R — упругие модули скелета и флюида, а также модуль их «связи», p11, p12, p 22, — комбинация плотностей скелета и флюида, причём предполагаются следующие соотношения с реальными плотностью скелета ps, плотностью флюида pf и пористостью среды в : p11 + p12 = ps (1 - в), p12 + p22 = epf • Функция F(к) описывает частотно зависимые диссипативные процессы при перемещениях жидкой компоненты относительно стенок открытых цилиндрических пор скелета в предположении гармонических по времени осцилляций под действием волны частоты f и определяет

— ( ber (0, к ) + ibei (0, к ))

ся через некоторую другую функцию T ( к ) = dk ------------------ следующей фор-

( ber (0, к ) + ibei (0, к ))

мулой: F ( κ ) =

1    κ T ( κ )

1 - ² T ( κ ) i κ

κ =   _f ^f _c ,

а f_c =

b 2 πρ ( γ ₁₂ + γ ₂₂)

— так называемая харак-

терная или критическая частота, ρ = ρ11 + 2ρ12 + ρ22 , b = 8µβξ/a2 , µ — динамический коэффициент вязкости жидкости, ξ — коэффициент, описывающий степень извили- стости пор, a — средний радиус пор, γ12, γ22 — безразмерные коэффициенты, опреде- ляемые соотношением плотностей обеих компонент среды. Из системы уравнений (1) может быть получено дисперсионное уравнение, связывающее фазовую скорость распространения волны с круговой частотой ω = 2πf . Дисперсионное уравнение для вели- чины, обратной квадрату фазовой скорости V распространения волн в безграничной двухкомпонентной среде,

α z 2 , Vα

P + 2 Q + R ^ρ

–– некоторая характерная ско-

рость, представим в обозначениях, используемых в цитируемой статье:

2                                                              2 ib

( σ ₁₁ σ ₂₂ - σ ₁₂ ) z ² - ( σ ₂₂ γ ₁₁ + σ ₁₁ γ ₂₂ - 2 σ ₁₂ γ ₁₂) z + ( γ ₁₁ γ ₂₂ - γ ₁₂ ) +     F ( κ )( z - 1) = 0 ,        (2)

ωρ где σ11,σ22,σ12 –– безразмерная комбинации модулей упругости скелета и флюида, образующих двухкомпонентную среду, γ11,γ22,γ12 –– аналогичная, упомянутая ранее безразмерная комбинация параметров плотности скелета и флюида.

Другая запись этого уравнения, используемая в [3], имеет следующий вид:

( z - z ₁)( z - z ₂) + iM ( z - 1) = 0 ,                                                                (3)

где z ₁ = V _α ² V ₁² , z ₂ = V _α ² V ₂² , V ₁, V ₂ ( V ₁ >  V ₂) –– фазовые скорости чисто упругих Р-волн 1-го рода (быстрая волна) и 2-го рода (медленная волна) в пористой среде, а величина ε + i ε

M =    ^{1   2}₂ , причём ε ₁ и ε ₂ –– величины, определяемые с точностью до множи-

σ 11 σ 22 - σ 12

теля реальной и мнимой частью функции F ( κ ), делённой на отношение частот f/ f_c .

Дисперсионное уравнение в форме (2) или (3) позволяет исследовать характеристики распространения акустических волн: фазовую скорость распространения волн сжатия как функцию частоты, а также получить соответствующую зависимость для коэффициента затухания волны. Фазовые скорости Р-волн двух типов по найденным решениям для z _1,2 определятся как c_{l 1,2} = V _α I Re z _1,2 , а коэффициенты затухания этих волн как α _1,2 = ω Im z _1,2 IV _α . При этом должны выполняться условия: c_{l 1} ( ω = 0) = V ₁ , c_{l 2}( ω = 0) = V ₂ . Отметим, что в настоящей работе основной интерес представляют различия перечисленных выше характеристик, относящихся к двум случаям –– к полностью флюидонасыщенной пористой среде, и к другому случаю –– к газонасыщенной среде с теми же упругими параметрами скелета, как и в сравниваемой флюидонасыщенной.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО АНАЛИЗА ПАРАМЕТРОВ РАСПРОСТРАНЕНИЯ И ВОЗБУЖДЕНИЯ Р-ВОЛН

Таким образом, обращаясь к решению уравнений (2), (3), будем иметь в виду рассмотрение двух практически интересных случаев: 1 –– среда с заполнением открытых пор жидкостью (водой) и 2 –– среда с заполнением пор практически невесомым, но упругим газом (воздух). В первом случае для того, чтобы получить приближённое соответствие пористым породам типа водонасыщенный песчаник или известняк [10] (плотностью скелета ρ 1 = 2,3…2,5 г/см ³ , скоростью в скелете Р-волн c l ≈ 3000 м/с), приняты следующие значения безразмерных упругих параметров σ ₁₁ = 0,88, σ ₂₂ = 0,088, σ ₁₂ = 0,016 и аналогичные безразмерные параметры плотности γ ₁₁ = 0,757, γ ₂₂ = 0,303 , γ ₁₂ = - 0,0303 . По оценкам в этом случае величина критической частоты, зависящая от кинематического коэффициента вязкости, от суммы γ ₁₂ + γ ₂₂ , от пористости и параметра извилистости, приходится на интервал от нескольких герц до первых десятков Гц. Характерная безразмерная скорость как в этом, так и во втором рассмотренном случае, нами принята равной V _α ≅ 3 км/с. Во втором случае, когда та же порода является газонасыщенной, аналогичные значения соответствующих параметров выбраны следующими: σ ₁₁ = 1 , σ ₂₂ = 0,000005 , σ ₁₂ = 0,000005 , γ ₁₁ = 1,0004, γ ₂₂ = 0,0004, γ ₁₂ = - 0,0004 , причём оценки показывают, что для газового заполнения пор критическая частота может находиться в интервале первых килогерц. Очевидно, что выбранные параметры моделей водонасыщенной и газонасыщенной сред могут лишь лучше, или хуже соответствовать наблюдаемым, например, в реальных экспериментах, но решаемая здесь задача состоит в сравнении качественного вида частотных зависимостей для коэффициента затухания и скорости распространения волн сжатия обоих типов в двух рассматриваемых ситуациях, которые предполагаются быть полученными в результате численных расчётов, опирающихся на теорию Био. Возможность интерпретации результатов численных расчётов также будет свидетельствовать о приемлемости сделанного выбора параметров. При решении уравнений (2), (3) использованы численные алгоритмы, входящие приложениями в пакет MATHCAD 2001. На всех частотных зависимостях, представленных далее графиками, по оси абсцисс отложена относительная частота, т. е. величина ω _отн = ω/ ω _с .

Так, на рис. 1а изображены две кривые коэффициента затухания, соответствующие двум указанным типам волн, которые показывают, что в среде с порами, насыщенными жидкостью, быстрая волна при распространении затухает существенно меньше, чем медленная волна. Степень затухания волн Р-2 на всех частотах расчётного интервала оказывается на порядок более высокой, чем у волн Р-1. Отметим стремление к нулю коэффициентов затухания обоих типов волн, проявляющееся в виде резкого падения обеих кривых вблизи нулевых значений частоты. Дополнительное исследование показывает, что характер стремления к нулю описывается с большой степенью точности зависимостью вида ~ω . На рис. 1б представлены соответствующие характеристики частотной дисперсии фазовой скорости распространения волн сжатия. Скорости рас- пространения волн Р-1 и Р-2 с ростом частоты асимптотически стремятся к некоторым постоянным значениям. Для волны Р-1 это значение несколько превышает характерную скорость Va, а для Р-2 оно примерно вдвое ниже Va. Сравнивая данные о затухании, можно заключить, что в такой среде в процессе распространения на больших удалениях от источника останется только Р-волна 1-го рода.

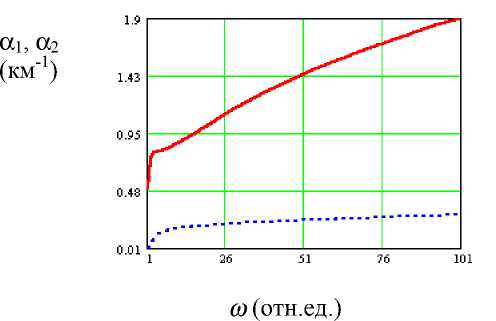
Рис. 1а. Зависимость коэффициента затухания Р-волн 1-го и 2-го рода от частоты в водонасыщенной среде волна Р-2 — сплошная кривая, волна Р-1 — пунктирная кривая

с l 1,              2999с l 2(км/с)       2499.25

1999.5

1499.75

1         26         51         76         101

а (отн.ед.)

Рис. 1б. Зависимость скорости распространения Р-волн 1-го и 2-го рода от частоты в водонасыщенной среде волна Р-2 — сплошная кривая, волна Р-1 — пунктирная кривая

На рис. 2а коэффициенты затухания Р-волн обоих типов в случае распространения в газонасыщенной пористой среде даны в виде константы, как результат практического совпадения этих двух величин. Тем самым показана их частотная независимость, примерное равенство, а также исчезающе малая их величина. На рис. 2б демонстрируются постоянные значения скорости этих волн, свидетельствующие об отсутствии дисперсии, но в отличие от примерного равенства параметров диссипации значения скорости распространения волн Р-1 и Р-2 сильно различаются величиной: c и ~ 3 км/с, c i₂ ~ 0,34 км/с. Из рис. 2а легко видеть, что ввиду одинакового значения коэффициента з атухания Р-волн 1 - го и 2-го рода нель з я отдать предпочтение при распространении ни Ю. М. Заславский

Об эффективности возбуждения быстрой и медленной волн Био в водо- и газонасыщенных средах хания Р-волн 1-го и 2-го рода нельзя отдать предпочтение при распространении ни той, ни другой волне.

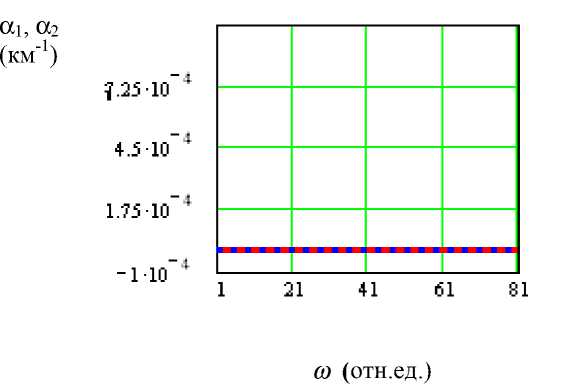
Рис. 2а. Коэффициенты затухания Р-волн 1-го и 2-го рода в газонасыщенной среде сплошная и пунктирная линии для волн Р-2 и Р-1 совпали

с l 1 , с l 2 ( км/с )

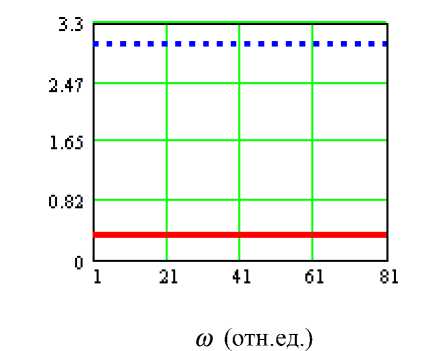
Рис. 2б. Скорости распространения Р-волн 1-го и 2-го рода в газонасыщенной среде волна Р-2 — сплошная линия, волна Р-1 — пунктирная линия

Далее целесообразно рассчитать амплитуду Р-волн обоих типов в произвольной точке наблюдения, возбуждаемых в безграничной двухкомпонентной пористой среде простейшим сосредоточенным в точке пульсирующим источником типа центр давления, а также мощность, уносимую упругим излучением в виде каждого из возбуждаемых типов волн, поскольку в случае поглощающей среды парциальные мощности излучения являются критерием эффективности работы источника. Предполагается, что указанный переменный во времени источник действует с заданной объёмной скоростью на твёрдый каркас и одновременно с некоторой в общем случае иной объёмной скоростью на флюид. Известно [5], что для описания упругих колебаний сжатия в двухфазной среде возможно введение двух скалярных потенциалов ф т,ф(2), с помощью которых волновые перемещения в сферически симметричном поле могут быть представлены следующим образом:

, , дф⁽¹⁾ дф ⁽²⁾ v = M_y — — + M, — —,

¹ д r ²  д r

u = дф ⁽¹⁾ + дф ⁽²⁾

д r      д r  ’ где r — радиус, соединяющий точки источник-приёмник; u, v — радиальные компоненты волновых перемещений в Р-волнах 1-го и 2-го рода (верхние индексы 1, 2) в твёрдом каркасе и в жидкой фракции соответственно, а комплексные коэффициенты M1, M2 даются выражениями [3, 5]:

M 1

- Y 12 + Z 1 ^ 12 - M ⁽ ^ 11 ^ 22 - ^ 12 )

Y 22 - Z 1 ^ 22 - ^{M (} ^ 11 ^ 22

-

^ 12 )

, M 2 =

- Y 12 + Z 2 ^ 12 - M ( ^ 11 ^ 22 - ^ 12 )

Y 22 - Z 2 ^ 22 - ^{M (} ^ 11 ^ 22

-

^ 12 )

.

Пространственная зависимость потенциалов ф ⁽¹⁾, ф ⁽²⁾, очевидно, должна иметь вид:

ф ⁽¹⁾ = A exp( ikl ₁ r ), ф ⁽²⁾ = B exp( ikl ₂ r ),

r

r

причём радиальные колебания каркаса u и флюида v в волне Р-1 и в волне Р-2, в соответствии с (4), запишутся как

AB u = — (ikl 1 r - 1)exp(ikl 1 r) + — (ikl2r - 1)exp(ikl2r),

r

r

AB v = M1 — (ikl 1 r -1) exp(ikl 1 r) + M2 — (ikl2r -1) exp(ikl2r).

r

r

Неизвестные коэффициенты A, B найдутся из условий для амплитуды объёмной скорости источника U0, действующей на каркас, и объёмной скорости V0, действующей на флюид, причём обе эти величины в общем случае не равны друг другу. Эти условия таковы:

U ₀ = lim _{r ч 0} - ко 4 n r u = i a 4 п ( A + B ),

V ₀ = lim _{r ч 0} - i a 4 n r ² v = i a 4 n ( M ₁ A + M ₂ B ).

Определяя из системы уравнений (8) коэффициенты A , B , приходим к выражениям для радиальных упругих смещений u , v в Р-1, Р-2 волнах:

u=

i ( V 0 - ^M 2 U 0 ) ( ikl 1 r - ¹) _exp( ik _r ) - i ( V 0 - ^M 1 U 0 ) ( ikl 2 r - ¹) _exp( ik r a (M ₂ - M ₁) 4 n r ^{2      P} l ¹     o ( M ₂ - M ₁) 4 n r ^{2      P} l ²

v=

iM 1 ( V 0 - M 2 U 0 ) ( ikl 1 r - 1) a (M ₂ - M ₁)    4 n r²

exp( ik_{l 1} r )

-

iM 2 ( V 0 - M 1 U o )( ikl 2 r - 1)

o ( M ₂ - M ₁)     4 n r ²

^exp^{( ik} l 2 ^r )•

Заметим, что волновые числа kl 1 , kl ₂ здесь определяются решениями уравнения (3) и каждое содержит как реальную, так и мнимую части, описывающие затухание волн. Представленные зависимости (9) упрощаются в предположении равных амплитуд объёмных скоростей, то есть при U ₀ = V 0 = Q . Для простейших условий работы пульсирующего источника — акустического монополя в однофазной упругой среде, которая рассмотрена, например, в работе [11], показано, что мощность, излучаемых им упругих Р-волн, даётся известной формулой:

2 А 2

W = рю Q

.

8 п с

Применительно к рассматриваемому случаю легко записать соответствующие выражения для излучаемой мощности волн Р-1, бегущих в скелете и во флюиде, и для мощности волн Р-2, распространяющихся по той же двухфазной среде, независимо от первых. Так, из формул (9) следует, что вместо объёмной скорости Q теперь для подсчёта мощности той части волны Р-1, которая бежит по скелету, необходимо использовать значение

Q

1 - M ₂

M ₂ - M 1

, а для подсчёта мощности волны того же типа, бегущей по флюи-

ду, следует принять выражение

Q

M 1 (1 - M 2 )

M ₂ - M 1

Аналогичная замена значений объёмных скоростей источника должна быть выполнена при подсчёте мощности, уносимой волной Р-2. В итоге приходим к выражениям для излучаемых мощностей в каждый из рассмотренных волновых типов:

W «= pg Q . 8 n ci 1	1 - м 2	2 +	M 1 (1 - M 2 )2
	м 2 - м 1		м 2 - м 1

1 - м ₁

W ⁽²⁾

рю ² Q ² м 2 (1 - м 1 ) ^{8 n} cl 2 I ^M 2 - ^M 1

+

м ₂ - м ₁

Частотные зависимости мощности излучения быстрых и медленных волн в водонасыщенной и в газонасыщенной среде рассчитаны с использованием соотношений (11) при одинаковых параметрах упругости скелета.

На рис. 3 а,б даны графики мощностей излучения W ⁽¹⁾, W ⁽²⁾, нормированные на

рд общий множитель -----Q , в зависимости от частоты ю, измеряемой в относитель-8ПС11,2

ных единицах. На рис. 3а представлен случай водонасыщенной среды, а на рис. 3б — случай газонасыщенной среды. Обращает на себя внимание наличие сравнительно узкого максимума в частотной зависимости нормированной мощности излучения обеих волн, характерное для случая водонасыщенной среды. Причём в указанном интервале частот пиковое значение W(2) = 2W(1), то есть мощность излучения источником мед- ленных Р-волн несколько превышает мощность быстрых волн. Однако, вследствие существенно большего затухания волны Р-2, наблюдаемой реально будет только волна Р-1. Кроме того, наложение характеристик излучения и поглощения приведёт к преобладанию узкого интервала частот в спектре уходящей волны при достаточной широко-полосности излучения источника. В этой связи можно напомнить об указании на возможность существования так называемых «доминантных» частот, встречающееся в некоторых работах [12]. Примерное равенство уровней мощности, излучаемой в виде упругих быстрой и медленной волн, имеет следствием то, что показатель затухания оказывается единственным критерием, позволяющим сделать заключение о доминировании волны Р-1 по мощности в водонасыщенной среде.

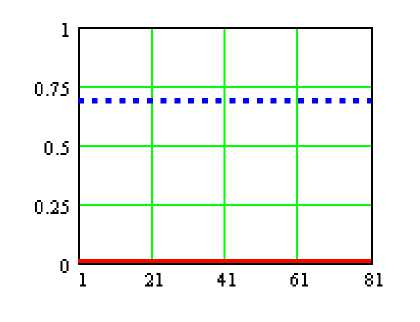
Для газонасыщенной среды двумя аналогичными независящими от частоты константами на графике рис. 3б представлены уровни мощности излучения волн Р-1 и Р-2 пульсирующим источником, причём W ⁽¹⁾ >>  W ⁽²⁾ (в относительных единицах, соответственно 0,684 и 0,002). Это обстоятельство позволяет говорить о преобладании в такой среде волн Р-1 над Р-2, поскольку показатели затухания здесь практически одинаковы и не могут служить критерием ввиду исчезающей малости их значения. Напомним, что в теории Био учитывается механизм диссипации, связанный только с потерями на взаимное скольжение жидкой фазы вдоль стенок пор. Таким образом, сопоставляя данные по эффективности генерации волн с данными по показателю волнового затухания, видим, что в противоположность случаю водонасыщенной среды решающей здесь является эффективность возбуждения волны.

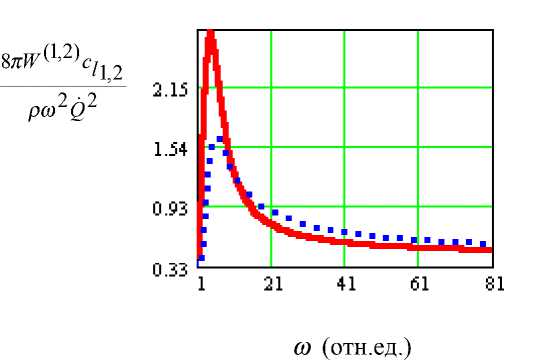
Рис. 3а. Частотная зависимость нормированной мощности излучения источника в водонасыщенной среде сплошная кривая — волна Р-2, пунктирная кривая — волна Р-1

pa 2 Q 2

_{8 π W} (1,2) _{cl 1,2}

ω (отн.ед.)

Рис. 3б. Нормированная мощность излучения источника в газонасыщенной среде сплошная кривая — волна Р-2, пунктирная кривая — волна Р-1

ВЫВОДЫ

Полученная совокупность данных облегчает прогноз экспериментальной наблюдаемости того или иного типа акустических волн в условиях реальных пористых сред, возможно близких к двум идеальным моделям (водонасыщенной и газонасыщенной) среды, применительно к которым справедлива общая концепция волн Био.

По результатам проведённого численного анализа могут быть сделаны следующие выводы, вытекающие из рассмотрения как этапа возбуждения волн источником, так и этапа распространения. В водонасыщенной пористой среде, преимущественно распространяющимся по ней типом волны является Р-волна 1-го рода. При одинаковой объёмной скорости источника, воздействующей на скелет и флюид, в газонасыщенной среде с теми же упругими характеристиками скелета, ввиду изложенного выше, также преобладает Р-волна 1-го рода. Для первого случая результат физически объясняется тем, что Р-волна 1-го рода не испытывает столь значительных потерь при распространении по влагозаполненной среде, как волна 2-го рода. Это происходит вследствие почти полной синхронности (синфазности) низкочастотных колебаний частиц на границе стенки и флюида, в то время как Р-волна 2-го рода подвержена значительной диссипации из-за противофазности колебаний твёрдой и жидкой фракции, т. е. вследствие взаимных перемещений частиц на границе. В случае газонасыщенности пористой среды существенно меньшая плотность газа обуславливает практическое отсутствие диссипации, то есть акустического затухания волн Р-1 и Р-2, и наличие этой фракции в порах не вызывает дисперсии фазовой скорости быстрой и медленной волн, хотя при этом сохраняется резкое различие самих значений скорости распространения.

Таким образом, выводы должны учитывать как эффективность излучения Р-волн обоих видов простейшим пульсирующим источником в безграничной пористой среде, так и сформулированные выше «приоритеты», связанные с мерой затухания волн. В Ю. М. Заславский

Об эффективности возбуждения быстрой и медленной волн Био в водо- и газонасыщенных средах водонасыщенной среде мощность излучения быстрой и медленной волн в среднем близки по величине, но имеет место различие по затуханию, а в газонасыщенной среде наоборот — при примерно равном, но ничтожном затухании обоих волновых типов, преобладает мощность излучения быстрой волны, что естественно и в этом случае приводит к доминированию в среде волны Р-1. При этом полученный результат имеет место только при условии равных значений объёмной скорости пульсаций источника, воздействующих на твёрдую и газовую фракцию.

Полученные результаты позволяют неформально подойти к пониманию трудно объяснимого, часто встречающегося в экспериментальной атмосферной акустике явления, заключающегося в чрезмерно завышенных регистрируемых уровнях проникания звука из воздушной среды в сыпучий грунт. Считая, что проходящая в грунт волна является волной Р-2, можно несколько снизить резкое различие акустических импедансов атмосферы и грунта. Дополнительно к этому необходимо ещё учесть существенное различие эффективной величины объёмных скоростей ( V ₀ >>  U ₀ в выражениях (9)) источника-громкоговорителя, работающего вблизи границы раздела сред и действующего в основном на газовую фазу. Вероятно, на этом пути следует искать разрешение известного парадокса.

Можно ожидать и практическую полезность выполненных исследований, например, применительно к анализу особенностей структуры и волнового состава упругих полей, создаваемых скважинными низкочастотными и среднечастотными виброисточниками в затрубном пространстве. Очевидно, что упругие поля скважинных источников, помещённых на глубину слоёв более насыщенных влагой или жидкими углеводородами, будут отличаться по характеристикам от полей источников, работающих в слоях, имеющих при той же степени пористости меньшее насыщение или полностью газонасыщенных. Поскольку с уменьшением или увеличением степени влагосодержания (ниже или выше некоторой пороговой) среда может рассматриваться или как газонасыщенная, или как водонасыщенная, к которым формально применима концепция Био, то справедливость такого утверждения следует из представленных результатов, относящихся к этим крайним случаям. Разница в волновых излучательных характеристиках может рассматриваться как физический признак степени флюидонасыщения среды, измеряемый экспериментально. Аналогичная ситуация возникает вследствие миграции жидкой фракции по области, занятой нефтезалежью. Там смена областей пространства с различной концентрацией флюидосодержания происходит в порах пласта при отборе флюида из коллектора. Таким образом, контроль состояния среды при нефтедобыче, вероятно, может выполняться с помощью сейсмоакустических методов, использующих излучение, последующий приём и анализ отражённых упругих волн. Очевидно, что на практике ситуация сложнее, ввиду того, что на соотношение амплитуд волн сжатия обоих типов будут сказываться не только параметры поглощения и характеристики излучения источником, но и процессы преобразования волн Р-1 в волны Р-2 и S- на границе разделов. Поэтому в дальнейшем целесообразно количественно оценить степень отражения и рассеяния, а также получить характеристики, связанные с взаимной трансформацией волн Р-1, Р-2 и с возбуждением S-волн на границе, разделяющей об- Ю. М. Заславский

Об эффективности возбуждения быстрой и медленной волн Био в водо- и газонасыщенных средах ласти с резкой сменой параметров насыщения среды, роль которых может оказаться решающей при проведении сейсмоакустического зондирования флюидонасыщенных областей в недрах. Первоначально один из вариантов соответствующего анализа был предпринят в статье [5], а в монографии [13] упоминается и о более поздних аналогичных работах. В настоящее время развёрнуты интенсивные исследования, затрагивающие, в том числе, и данную тему [14]. Получение таких результатов является столь же важным для практики, как изучение параметров скорости, затухания и условий оптимального возбуждения рассмотренных сейсмоакустических волн.

Работа выполнена при поддержке РФФИ (грант № 02-02-17089) и Shell International (проект № 2067/СР-1429 МНТЦ).