Об эргодических свойствах однородной марковской цепи
Автор: Головнева Елена Вячеславовна
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 1 т.14, 2012 года.
Бесплатный доступ
Изучен спектр бесконечномерной колмогоровской матрицы, по крайней мере, с одним отделенным от нуля столбцом. Показано, что нуль является собственным значением единичной кратности, а весь остальной спектр отделен от нуля. Соответствующий марковский процесс экспоненциально быстро сходится к финальному распределению; дана явная оценка скорости этой сходимости.
Марковские процессы, генератор, спектр матрицы, финальный проектор.
Короткий адрес: https://sciup.org/14318369
IDR: 14318369 | УДК: 512.643.5+519.217
Текст научной статьи Об эргодических свойствах однородной марковской цепи
Со времени работ Перрона и Фробениуса [2, 3] по изучению спектра положительных матриц, главное внимание было сосредоточено на изучении наибольшего по модулю собственного значения, в то время как задача отделения спектра от нуля практически не рассматривалась. Целью данной статьи является доказательство того, что для некоторого типа Колмогоровских матриц нуль является изолированной точкой спектра, а сами эти матрицы являются, соответственно, генераторами марковской полугруппы в пространстве l i , экспоненциально быстро сходящейся к одномерному проектору.
Основные положения теории марковских процессов со счетным множеством состояний и связанных с ними полугрупп в пространстве l i хорошо представлены в имеющейся литературе [4-7]. Мы же только напомним, что марковский процесс P (t) = e Qt однозначно определяется своим генератором Q. Условимся представлять оператор Q в виде матрицы, действующей справа налево на вектор-строку, принадлежащую пространству l i . При этом матричные элементы удовлетворяют условиям Колмогорова:
qii = — qij, qij > 0, j = i- j=i
В данной работе мы рассматриваем только генераторы конечной li-нормы kQk sup^ ^ij l> i j откуда очевидно следует, что все элементы матрицы, включая диагональные, конечны.
Для начала докажем одно полезное вспомогательное утверждение.
Предложение 1. Пусть дана ограниченная (как оператор в l i ) матрица A, для которой существует 6 > 0 такое, что
| a nn | > У^ | a nk 1 + 6 ( V n).
k = n
Такая матрица задает в пространстве l i обратимый оператор, иными словами, А = 0 не является точкой ее спектра. При этом норму обратного оператора A -1 можно оценить так:
k A -1 k 6 k A k . δ 2
C Рассмотрим равенство
A = diag(an, a22,...) + A, где A — матрица с нулевой диагональю, вне диагонали совпадающая с A, а diag(aii, a22,...) — матрица с нулевыми внедиагональными элементами. Далее рассмот-^^ ^^
рим матрицу A, определяемую соотношением A = diag(a ii , a 22 ,...) • (I + A). Очевидно, ^^
что k-ая строка A получена делением k-ой строки A на a kk . Оценим операторную нор- ^^
му A
III I akj I/ lakk| — § § § kAk = sup > lakj | = sup > --- 6 sup--:----:-- = 1--:----г 6 1 — т—тт.
k . k । akk । k |akk| suP |akk| kAk j j 6=k
Поскольку k A k < 1, существует обратная к A матрица
∞
/2 ( — A) )• diag(a -1 ^V--), m =0
где A0 ≡ I , а ряд сходится по операторной норме. Имеем kA-1k
m
1 6 kAk 6 kAk inf |aii| § • inf |aii| §2 ’
где в последнем переходе мы использовали очевидное неравенство inf | ац | > §, несколько ухудшая возможную точность оценки. B
Заметим, что в конечномерном случае утверждение о существовании обратной матрицы по сути дела эквивалентно классической теореме Гершгорина [8, 9]. Более того, матрицы с диагональным преобладанием достаточно интенсивно изучаются в литературе, по крайней мере, в конечномерном случае [10, 11]. Но нам в дальнейшем пригодится не только экзистенциальный результат, но и сам подход с разложением в матричный ряд, равно как и следующая из него оценка нормы обратного оператора.
Основной целью данной работы является применение этого метода к исследованию одного класса марковских процессов с непрерывным временем. А именно, рассмотрим такой ограниченный генератор Q, что его матрица содержит столбец, все элементы которого равномерно отделены от 0:
( 3 k) ( 3 § > 0) : ( V j) Iq jk l > §.
С помощью предложения 1 можно не только установить эргодические свойства так определенного класса процессов, но и получить для них несложные доказательства ряда общих утверждений теории марковских процессов, сформулированные на языке элементарных свойств матриц без обращения к понятиям теории вероятности. Например, из общей теории марковских процессов известно, что точки с Re А > 0 не принадлежат спектру оператора Q.
Лемма 1. У оператора Q нет точек спектра с Re А > 0 , кроме А = 0 .
<1 1) Рассмотрим А = ге, е Е R , и оператор Q + А1 .
q nn Е R ^ V е Е R lq nn + ге | = V q nn + е 2 .
Рассмотрим
| q nn + ге | 2 - | q nn | 2 = ( | q nn + ге | - | q nn | )( | q nn + ге | + knn l )-
С другой стороны, это выражение равно qnn + е2 — qnn = е2. Кроме того, 11„„„
|qnn| = У^ |qnk1 = 2 У^ |qnk1 6 2 ||Qk-n=kk
Поэтому е2
1 q nn + ге| — Ы = | q nn + ге | + ^пп | > k Q k + ^ ^ + ^ ( V n Е N).
Осталось лишь заметить, что в силу доказанного
2 lqnn + ге| > У Ы +-------,, nA + 4 +. ■
-
и к матрице Q + ге1 применимо предложение 1. 2) Случай положительной вещественной части еще проще. Поскольку q nn < 0, то
при Re А > 0 имеем lqnn — А| = V(|qnn| + Re А)2 + (Im А)2 > |qnn| + Re А-
Дальнейшее рассуждение очевидно. B
Предложение 2. Область
Re А >
(Im А) 2 йгтТ^)2^ ^^
принадлежит резольвентному множеству Q.
-
< Утверждение следует из доказательства леммы 1 с учетом элементарного неравенства
| q nn — А | > | | q nn — iIm А | — | Re А | | • >
Теорема 1. Генератор Q, с отделенным от нуля столбцом и конечной нормой, порождает марковскую полугруппу, экспоненциально быстро сходящуюся равномерно к однозначно определенному финальному распределению.
Утверждение теоремы является следствием серии доказанных ниже лемм 2–7, которые утверждают, что для генератора Q значение А = 0 является изолированной точкой спектра (собственным значением единичной кратности), и все остальные точки спектра имеют Re А < 0.
По условию существуют к и 6 > 0 такие, что для любого j выполняется | q jk | > 6. Без нарушения общности будем считать, что к = 1. Очевидно, что матрица B , получаемая из Q удалением первой строки и первого столбца, удовлетворяет условию предложения 1.
Лемма 2. Спектр матрицы B не пересекается с кругом | λ | < δ .
-
<1 Для доказательства леммы покажем, что оператор B — XI обратим при любом | λ | < δ . Действительно,
Ы > ^>n3 | + 6.
j 6 =n
Следовательно,
| b nn - X | > | b nn | - | X | > ^^ | b nj 1 + 6 - | X | .
j 6 =n
Применив к матрице B - Iλ предложение 1 с δ - | λ | вместо δ , получаем, что существует оператор (B — XI ) -1 . B
Заметим, что норма оператора (B — XI ) -1 оценивается следующим образом:
k (B — XI ) -1 k 6
k B - λI k .
(6 — | X | ) • inf | b ii — X |
Для выяснения вопроса о спектре оператора Q в окрестности X = 0 рассмотрим связь операторов Q и B :
Q =
q 11 ~
~e
fB
где q 11 отрицательное число, ~e может действительно рассматриваться как элемент l 1 , поскольку | qn | = ^i=2 | e i | , а f принадлежит лишь 1 Ю . B — обратимый оператор, все точки спектра которого удовлетворяют неравенству | X | > 6 (см. лемму 2).
Лемма 3. Необходимым и достаточным условием того, что X = 0 является точкой спектра оператора Q, служит соотношение qn = eB -1 f.
-
< Выясним, при каких условиях оператор Q имеет обратный. Фиксируем m Е 1 1 и перепишем вектор m в виде m = (m 1 ,fn ), где m = (m 2 , m 3 ,...). Найдем вектор p Е 1 1 , p = (p 1 ,p), такой, что pQ = m. Если это можно сделать однозначно для любого m Е 1 1 , то существует обратный Q -1 . Матричное уравнение
( p 1 , p~ )
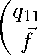
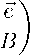
= ( m 1 , m~ )
можно записать покомпонентно q11p1 + p~f~ = m1, p1~e + ~pB = m~ .
Здесь p~f~ понимается как действие функционала f~ ∈ l ∞ на вектор ~p ∈ l 1 или как формальное евклидово скалярное произведение, которое сходится, поскольку
∞∞ ∞ и =
X p i f i 6 X | p i f i | 6 sup | f i | x | p i | 6 k Q kk p k .
i =2 i =2 i i =2
Из второго уравнения находим p~ = (m~ — p1~e)B-1
и подстановка в первое уравнение дает
(qii - eB 1~)pi = mi - mB i~, где все операции определены корректно по той же причине, что и умножение ~p на f~. Полученное уравнение имеет решение при любом m тогда и только тогда, когда коэффициент при p1 не обращается в нуль. Если решение существует, то оно очевидно принадлежит l1 . B
Лемма 4. Если A = 0 является точкой спектра оператора
Q =
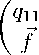
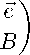
где e Е l i и B имеет обратный, то A = 0 является собственным значением кратности 1 .
C Утверждение следует из того, что критерий существования собственного вектора tQ = 0 для нашего оператора совпадает с условием из леммы 3. Действительно, пусть или покомпонентно
что эквивалентно системе
I
Поскольку равенство ~В = 0
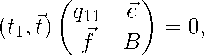
I
q ii t i + ~f = 0, t i e + ~B = 0,
q ii t i - t i ~B - ff = 0, ~ = — t i eB -i .
по условию невозможно, имеем t i = 0 и q ii = eB f , а
вектор t определен однозначно. B
Заметим, что генератор Q из условия теоремы В самом деле, Q удовлетворяет условию ^2k q ik = матричному уравнению
имеет собственное значение A = 0.
0 при любых i, т. е. формальному
Q
.
.
.
VJ
= 0 ,
которое может быть записано в виде двух условий:
q ii + ^X e i = 0, J + B
i
.
.
.
= 0.
VJ
Отсюда следует
B --1 f =
-
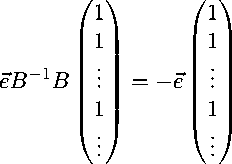
- ^ei = q ii - i
Поэтому A = 0 есть собственное значение в силу леммы 4.
Рассмотрим теперь оператор Q - λI , где | λ | < δ.
Q — AI =
q 11 - A
—*
f
e
B - λI
Оператор B - λI имеет обратный в силу леммы 2. Для дальнейшего нам необходимо установить некоторые свойства оператора (B — AI) -1 .
Лемма 5. Пусть λ — вещественное число, λ > - δ . Тогда все элементы матрицы (B — A) -1 неположительные.
-
<1 Действительно, по предложению 1 обратный оператор к B — A существует и представим в виде сходящегося по операторной норме ряда
(^
X ( — B ) V diag ( (b ii — A) 1 , (b 22 — A) 1 ,... ) .
m=0'
^^
При этом очевидно, что все элементы матрицы B неположительные. Значит, матрица ^^^^
( — B) > 0. Таким образом, ( — B ) m > 0 для всякого m, в то время как все диагональные элементы исходной матрицы отрицательны. Отсюда, очевидно, следует утверждение леммы. B
Замечание 1. Комбинируя лемму 5 в случае A = 0 с явным выражением для собственного вектора, найденным в лемме 4, видим, что этот вектор (вектор финальных вероятностей) действительно допускает вероятностную интерпретацию, поскольку, выбрав t 1 > 0, имеем t i > 0 при любых i.
Лемма 6. Оператор Q не имеет вещественных элементов спектра, удовлетворяющих неравенству λ > - δ .
-
< Допустим, что это не верно. Рассмотрим оператор Q [A] = Q — AI. Если A является элементом спектра для оператора Q, то точка 0 будет элементом спектра оператора Q [\ Следовательно, по лемме 4 получаем
9 11 — A = ~(B — AI) 1 f.
Однако нам также известно, что qn = ~(B) f,
— (B ) -1 f =
..
После несложных подстановок и преобразований с использованием резольветного урав- нения (B — XI) 1 — B 1 = X(B — XI) 1B 1 получаем
1 = e(B — XI ) -1
.
. .
1 ...
В соответствии с леммой 5, все элементы (B — XI ) -1 неположительны, а все компоненты e неотрицательны по условию. Следовательно, последнее равенство не может быть верным. Получено противоречие. B
Осталось убедиться в отсутствии комплексных точек спектра в проколотой окрестности нуля.
Лемма 7. У матрицы Q нет точек спектра вида X — ег, где X, б G R , таких, что | е | • k (B — XI ) -1 k < 1 .
C Заметим, что если такие точки в спектре существуют, то они входят в него парами, т. е. точками спектра будут (X — ег) и (X + ег). Допустим, что существует такая пара. В этом случае выполняются следующие соотношения:
q 11 — X — бг = e ( B — (X + бг) I ) f, q 11 — X + ег = e ( B — (X — ег) I ) 1 f.
Известно также, что
1 11 = eB -1 f,
-
B -1 f =
1 1
.
. .
1 ...
откуда, несколько раз используя резольвентное уравнение, нетрудно получить
e(B — XI ) ( (B — XI ) 2 + 6 2 I ) 1
= 1 .
..
Рассмотрим оператор (B — XI ) ( (B — XI ) 2 + е 2 1 ) 1 . В силу условия леммы он допускает разложение в сходящийся ряд
(B — XI ) ( (B — XI ) 2 + 6 2 I ) 1 = (B — XI )(B — XI ) -2 ( I + 6 2 (B — XI ) -2 ) 1
= (B — XI ) -1 • J2 ( — 1) k е 2к (B — XI ) -2k .
k
В результате получаем
∞
1 = e X ( — 1) k (B — XI ) -(2k+1) , 2k k=0
.
.
.
..
Заметим, что у нечетных членов (с четным к) этого ряда все матричные элементы неположительные в силу леммы 5, а у всех четных — неотрицательные в силу множителя ( — 1). Но поскольку ||e 2 (B — XI ) -2 Ц < 1, то исходя из явного выражения для принятой операторной нормы, легко убедиться, что сумма элементов любой строки каждого члена этого матричного ряда строго меньше по абсолютной величине суммы элементов той же строки предыдущего члена. Следовательно, величина, стоящая в правой части равенства, отрицательна. Получено противоречие. B
-
<1 Доказательство теоремы 1. Мы доказали, что у оператора Q отсутствуют точки спектра в областях комплексной плоскости, определяемых предложением 2 и леммой 7. Следовательно, спектр Q не может лежать правее точек пересечения границ этих областей. Вещественная часть этих точек пересечения, обозначим ее — X * , и задает скорость выхода на финал: ||e Qt — lim T ,^ e QT | убывает не медленнее, чем e -A * t . B
Легко получить в явном виде несколько грубую оценку величины X*. В самом деле, поскольку kB — XI|| > sup |bii — X| > inf |bii — X| > 6 — |X|, ii имеем оценку kB — XIk-1 6 Дуг
-
6 — | X |
(см. замечание после леммы 2). Соответственно условие из леммы 7 запишется в виде | e | + | X | 6 6. Для простоты огрубим также условие из предложения 2 до
Re X >
(Im X) 2
k Q k + 1 Im X |
или в текущих обозначениях
X>
e 2 k Q k + | e | '
Легко убедиться, что вещественная часть точек пересечения границ этих областей выглядит следующим образом:
—X *
— 6
-
k Q k — 6
-
,I ( k Q k— 6 ) 2 . k QP
16 + 2
или, после преобразований
-
X *
-
k Q k
1+3 k Q k
-
.
Заметим, что последнее равенство, в пределе малого δ , можно оценить более простым выражением
= _ 1W
8 k Q k
+гал (кт)1
дающим явную и легко вычисляемую по явному виду генератора, оценку скорости схо- димости процесса.
Рассмотрим два примера, иллюстрирующих нашу теорему. В первом случае генератор Q = (q ij ) задается следующим образом:
q ii = - 1, q i2 = i, q 2i = q 22 = -^, qn = ——, q ii = -——
2 2 i i
Здесь первый столбец отделен от нуля числом 2 , а норма оператора Q равна 2. В этом случае легко разрешаются уравнения Чепмена — Колмогорова P (t) = QP (t), и можно в явном виде выписать все функции p ij (t):
, ч 1 2 _з. . . 2 2 _з. А ., . „ pii(t) = 3 + 3 - 2, pi2(t) = 3 — з e 2, pij = o (vj > 3),
P 21 (t) = 3 — 3 e - 2 t , p 22 (t) = 3 + 3 e - 2 t , P 2 j =0 ( v j > 3),
|
p ii = e - |
i -1 t i |
( v i > 3), |
|
|
1 |
4(i — 1) - |
i — 2 _i-i. |
|
|
p ii = 3 |
3(i + 2) |
2 + |
e i t i +2 |
|
2 |
, 4(i — 1) |
3 t |
2i _i-i. |
|
p i 2 = 3 |
3(i + 2) |
e i t i+2 |
|
( v i > 3),
(vi > 3), pij = 0 (V i,j : 3 6 j < i или j > i > 3).
В данном примере видно, что финал достигается экспоненциально быстро, а именно
|| e Qt - lim T ^e QT || = O ( e 3 t ) .
Во втором случае Q = (qij), где qii = —1 qi2 = 1 q2i = -, q22 = —-, qii = -, qii = —г.
2 2 i i
В этом примере нет отделенного от нуля столбца. Уравнения Чепмена — Колмогорова решаются в полной аналогии с предыдущим примером.
p ii (t)=3+3 e - 2 t , p i2 (t)=3 - 3 e - 2 1 , p ij =o ( v j > 3)
P2i(t) = 3 — 3 e-2t, p22(t) = 3 + 3 e-21, p2j = 0 (v j > 3), pii = e-i (vi > 3),
1 4 _з, i — 2 _t _ pii = 3 — 3(31—7)e 2 — 31—7e i (vi > 3),
-
2. 4 _з, 2i _
pi2 = 3 + 3(3i—7) e 2 - 3i—7 e i (vi > 3), pij = 0 (v i,j : 3 6 j < i или j > i > 3).
В данном случае легко заметить, что хоть финальное распределение и существует, но сходимость к нему не равномерная.
Заметим, что другим подходом, в рамках которого возможно изучение спектра Марковской полугруппы, является изучение свойства позитивных полугрупп в полуупорядо-ченных банаховых пространствах [6]. Основы теории этих пространств были заложены еще В. Л. Канторовичем [12]. В плане развития данной работы планируется применение теории поуупорядоченных банаховых пространств к изучению эргодических свойств Марковской полугруппы.
Автор благодарит профессора В. П. Одинца за постановку задачи и плодотворные обсуждения.
Список литературы Об эргодических свойствах однородной марковской цепи
- Воробьева Е. В. О некоторых эргодических свойствах однородной марковской цепи с непрерывным параметром//Вестн. Сыктывкарского ун-та. Cер. 1-2006.-Вып. 6.-С. 39.
- Perron O. Zur Theorie der Matrizen//Math. Ann.-1907.-Vol. 64.-P. 248-263.
- Frobenius G. Uber Matrizen aus nichtnegativen Elementen//Akad. Wiss.-1912.-P. 456-477.
- Булинский А. В., Ширяев А. Н. Теория случайных процессов.-М.: Физматлит, 2003.-399 c.
- Хилле Э., Филлипс Р. C. Функциональный анализ и полугруппы.-М.: ИЛ, 1962.-830 с.
- Клемент Ф., Хейманс Х. и др. Однопараметрические полугруппы.-М.: Мир, 1992.-352 с.
- Ланкастер П. Теория матриц.-М.: Наука, 1982.-269 с.
- Gerschgorin S. A. Uber die Abgrenzung der Eigenwerte einer Matrix (German)//Изв. Академии наук СССР. Сер. 7. Отделение математических и естественных наук.-1931.-Вып. 6.-С. 749-754.
- Колотилина Л. Ю. Множества, содержащие сингулярный спектр квадратной матрицы//Численные методы и вопросы организации вычислений. XXI, Зап. научн. сем. ПОМИ.-СПб., 2008.-Т. 359.-С. 52-77.
- Колотина Л. Ю. Проблема вырожденности/невырожденности для матриц, удовлетворяющих условиям диагонального преобладания, формулируемым в терминах ориентированных графов//Численные методы и вопросы организации вычислений. XVII, Зап. научн. сем. ПОМИ.-СПб., 2004.-Т. 309.-С. 40-83.
- Канторович Л. В., Вулих Б. 3., Пинскер А. Г. Функциональный анализ в полуупорядоченных пространствах.-М.-Л.: Гостехиздат, 1950.-550 с.


