Об оценке устойчивости и погрешности разностной схемы в задаче оптимального управления для линейного уравнения Шредингера

Нахичеванский государственный университет (Азербайджан)

AZ7012, Нахичевань, ул. А. Алиева,1

Рассматривается задача оптимального управления для линейного уравнения Шредингера с критерием качества Лионса. К этой задаче применяется разностный метод. Устанавливается оценка устойчивости и погрешности разностной схемы, исследуется вопрос об оценке скорости сходимости разностных аппроксимаций по функционалу. Подобные вопросы освещены в работах [1-4] и др.

Постановка и дискретизация задачи

Рассмотрим задачу о минимизации функционала

J(v) = f 1^1 (x, t) — К (x, t) 2 dx о на множестве

V = { _v = v ( x ) : v e W / ( 0, l ),

I v (x )< b 0,

dv (x )

dx

< b, V x e (0, l)

>

при условиях

dyn   d \

i - + a 0 "ГТ - a(x Кр - v (x К = fP (x, t), (x, t)e n ,(2)

dt     dx

К p (x ,0)= ^p (x), p = 1,2, x e(0, l),(3)

К1 (0, t) = К1 (l, t) = 0, t e(0, T),(4)

вк(0р   ^yp(^ = 0, t _{e( 0}, T )

dxdx где i2 = -1, a0 > 0, b0 > 0, b > 0 - заданные числа, Q = (0, l )X(0, T), a (x) - ограниченная измеримая функция, удовлетворяющая

а функции p k ( x ), f_k ( x , t ), k = 1, 2 , удовлетворяют условиям

^1 e W23 (0, l), ^! (0) = ^ (l) = ^ (0) = ^ (l)= 0, p, e W2(0,l), d^ = -^44 = 0,(7)

dxdx

01.1

f. e W2 (a),f, eW"(n)       eL,(<4p = 1,2, (8)dxdt

^ >  0, i = 0, 2 - заданные числа.

При каждом заданном v e V под решением редуцированной задачи (2)–(5) понимаются функции

К e B 1 - C ⁰( [ 0, T ] W₂² ( 0, l ) ) П C ’( [ 0, T ] L ₂ ( 0, l )) , К 2 e B 2 - C ⁰ ( [ 0, T ], W 2 ² ( 0, l ) ) П C ’( [ 0, T ] L 2 ( 0, l )) , удовлетворяющие соотношениям (2)-(5) для почти всех x e ( 0, l ) , V t e [ 0, T ] .

Исходя из результатов работы [2] можем утверждать, что редуцированная задача (2)-(5) имеет единственное решение К e B , y ₂ e B₂ и верны оценки

условиям

0 < ^ < a (x )< щ,

da ( x ) dx

< ^, , V x e ( 0, l ) ,(6)

I Н, t ) W 2 (0, i ) +

^д К 2 ⁽ ~ , t ) д t

L (0, l )

< M 1 ,

I ^К 2 ⁽ - , t )l W ^(0, l ) ⁺

dy 2 ⁽ - , t ) dt

< M ₂ (10)

L 2 (0, l )

для V t е [ 0, T ] , где М₁ >  0 и М₂ >  0 - постоянные величины, которые не зависят от t , но зависят от остальных исходных данных задачи. Из условий (6)-(9) следует, что функции a ( x ) , ф_к ( x ) , f_k ( x , t ) , k = 1,2 , являются

гладкими, поэтому при v e V с помощью результатов работы [2] можем определить сле

дующие оценки:

I Ы’t )|fc(0, l ) ⁺

d f iG t ) д t

^- M 3 [| Ы\^ ) к

I k 2⁽ - , t )| W 23 (0, i ) ⁺

+

L 2 (0, 1 )

+ 11/111 01,1 +

II⁷¹ W 2 ( П )

дгМ д t

+

L 2 (0, 1 )

- ^М 4 1 Ы W 23 (0, l ) ⁺lI f J W ;,> ) ⁺ к

^д V i⁽ - ’ t ) д x д t

д ² f ( - , t ) д x д t

kA д x д t

-

L 2 (0, l )

L 2 (0, l ) J

-

L ₂(0, l )

ft) д x д t

L 2 ( H ) J

(12) для V t е [ 0, T ] .

Произведя дискретизацию при каждом натуральном n >  1 , рассмотрим задачу о минимизации функции

N М -1             ₇

I n ( [ v ] n ) = T ZEh 1 k -^Фк     (13)

k = 1 j = 1

x j + h/ 2

ЫР = 7 jЫ(x)dx, j = 1,M-1, p = 1,2, Ы = kM = 0, x•- h/ 2

^s- x rf = ^s- x ^ M = ⁰’         (19)

I tk xj+hl2                            ____________ ______ fp = У J  ffp(x,t)dxdt, j = 1, M-1, k = 1,N, p = 1,2.

x^ ²

Эти функции определены на сетке

^{{ (} x j ’ t k ) n } n = ^0,1,2

',....,

x₂ = jh - h/ 2, t_k = kr,

j = 1, Mn -1, k = 1, Nn, h = hn = l/ (Mn -1) ’ т = T = T/N., ^Ф pk =

= ( Ф pk —Ф P, - 1)/ T , S x Ф pk = ( Ф J -Ф ' - 1 k )/ h

Sx Ф k =(ф p+1 k -Ф pk )/h ’ s ф ; =(ф p.1 k - 2ФPk +фp-1 k)/h2, p=1,2.

Обозначим M = M_n , N = N_n

С помощью сумматорных тождеств не-

трудно доказать справедливость утверждения.

Теорема 1. Для решения разностной схемы (14)-(17) при [ v ]„ е V_n верна оценка

m - 1              Mm - 1    ,       n m - 1

2                        2                      2

IФ pm - M 5 hE j + TEE^i| j=1                   к j=1               k=1 j=1

P

, p = 1,2 ,

J

на множестве

Vn ^[v] n:[v] n =( v 1’ v2’...’ vM-1) vj - b 0’j =1,M-1, M-b1’ j = 2, M — 1? при условиях i3tФp]k + asфp -aJфPk -VjфPk = j,  (14)

j = 1, M - 1, k = 1, N ,

Ф^ = Ы , J = 0,M, p = 1,2,(15)

Ф0k =ФMk = 0, k = CN,(16)

s x ф 2 k = s x ф M = 0, k = 7 N ,

где сеточные функции a , ы р , f p , p = 1,2 , определены следующими формулами:

a ¹ i_h

x j + h / 2

j a ( x ) dx , j = 1, M - 1 ,   (18)

x j - h / 2

(21) для любого m е { 1,2,..., N } , где M ₅ >  0 -постоянная величина, не зависящая от h и т .

Оценка погрешности разностной схемы

Оценим погрешность аппроксимации. С этой целью рассмотрим следующие усреднения решения редуцированной задачи (2)-(5) при v e V :

К(x ’ t; v)] n =kp },kjk = xj + h/ 2

= - f  kp (x, tk )dx, j = 1,M-1, k = 1,N, h xj -h/2

kj₀ = k j , j = 0, M , p = 1,2 , k J k = k Mk = ⁰ ’ k 0 k = k u ’ k Mk = k M -1 k ’ ^k =I N .⁽²²⁾

Определим оператор Q на множестве V по формуле x,+hi'2

j

Q n ⁽ v ) = { w j } , w j =7 \ v ⁽ x ) dx , ^j = 1, M - 1. ⁽²³⁾

h x j - h '2

Обозначим

[ z^p ] _n = { z pk } = { ^ф k }^-{ fy Jk } • Ясно, что { z^Pp_k } будет решением следующей системы:

где

1 ^{t k}' ^x,th ² a₀dfy

F p ¹ = 7                dxdt - a ■• fy , (33)

'     ^л; . 1 . , Д, 2 ^{d x}                    '

I t k ^xJ + hl ²

F jk ² = - T f  J ^{v ( x fy} _p ^dx^dt + ^v j fy^ k ,

Th / tk-1 xj- h2

J = 17 M - 1 k = 17 N , p = 1,2 ,   (34)

p     p   p   pp i°tZJk + a0dxxZJk - aJZJk - vjzjk = Fjk , ________ ____ (24)

j = 1,M-1, k = 1, N ,

z^ = 0, J = 0, M , p = 1,2 ,    (25)

I t k x j ⁺ h ²

F jk 3 = 7 j  I a ^{( x fy}p ^{( x} , t ) ^{dxdt -} a fy jk ,

^{T h} t k - 1 x j - h/ 2

где

p

F jk

z 1 k = Z Mk = 0, k = 17 N ,   (26)

^ x z 1 k = Я- x z M = 0, k = 1, N ,    (27)

t_k^x j ⁺ h ² (

^t k   ^xj

7,72 1

^d 2 V_P a

⁰ d x ²

- a ( x fy - v ( x fy dxdt + J

⁺ v j fyk - a 0 $ xx fy k ⁺ a fy k ,

j = 17 M - 1, k = 7 N , p = 1,2 .    (28)

Теорема 2. Пусть выполнено условие

т согласования c0 < — < c, где c0, c > 0 -0     h2      1             0      1

постоянные, не зависящие от h и т . Тогда верны оценки

M - 1

h S|zjm\ < M 6 T + h + l Qn (v)-[v] nil Л j =1

P = 1,2 , для V m e { 1,2,..., N } , где

M - 1

II Q n ^{( v ) -[ v} ] . 1 1= ^h S| w

< j = 1

-

v j J .  (30)

Доказательство. Аналогично оценке (21) легко доказать справедливость оценки

M - 1    ₉       ( N M - 1    7

h 2 z’A <  M 7 Th SSI J ,P = 1,2 , (31)

M - 1

j = 1

V    k = 1 j = 1         J

V m e { 1,2,..., N } .

Оценим правую часть неравенства (31).

Используя формулу для F p , p = 1,2 , эту оценку можно представить в виде

p       p 1        p 2        p 3

¹ jk ¹ jk ^{+ 1} jk  ^{+ 1} jk ,

j = 1, M - 1, k = 1, N ,(32)

J = 17 M - "1, k = 1,7, p = 1,2 .   (35)

Используя формулы (34),(35), а также (20),(21) для слагаемых Fp2 ,Fp3 , можно по лучить справедливость неравенства

I F l 2Г <  2 M .| W

b 2 т +   '

h

t_k ^x i + h ²

1 j tk-1 xj- hl2

—

^d fy d t

„ к 2 к t k ^xJ + hi ²

+ т 11

t k - 1 x j - h ²

dxdt ,

^d W p d x

dxdt +

j = г; m - 1, k = 1, N , p = 1,2 ,  (36)

_n 2    t_k^x j ⁺ h ²

I Fk 3r < 2F j I tk-1 xj - h 2

_Л 2 t, x, + h/ 2

+2 * 7 11

t k - 1 ^x j - ^{h 2}

d^ p C x ^ t )

d t

3fy p ^{( x} , t ) d x

dxdt ,

dxdt +

j = 17 m - 1, k = 1, N , p = 1,2 .    (37)

Оценим слагаемое F^p_k ¹, p = 1,2 . Предварительно оценим значения F ¹¹ при

j = 2, M - 2 , k = 1, N . С помощью формулы

(33) находим

,   tk x j + h ²

F jk = 4 J J

Th / tk-1 xj - hl2

o ^dM _dxdt - d x ²

—

a

h

x j + 1 ⁺ hl ²

x_j + h/ 2

j fy ( x,t_k ) dx - 2 j fy ( x,t_k ) dx +

x j + 1

- h / 2

x_j - h/ 2

x^_ ]+ h / 2

+ J< (x ,tk)dx x,—1— h/2

1 t k ^xj ⁺ hl ²     _Л2,„ I X

1 г г d <  ( x , t )

= -      a.---dxdt h, L0  dx2

t k — 1 ^x j ^— h! ²

—

t k   X j + 1 + hl 2

a0r     j ^ j ( x , t ) dx

™ L t k - 1 X j + 1 - h 2

—

t_k x j ^{+ h 2}

— 2 J J < (x, t) dxdt + tk—1 xj—h!2

t k x j — ¹ + hl ²

J   J <  ( x , t ) dxdt >

t k — 1 ^x j — 1

— h/ 2

—

tk

^x, ⁺ hi ² Г x + ht k

<

id J J JJ

t k _— 1 x , — h/ 2 _l x t

t

д?^

acdu —

д^дд 5

x d< fa) 1 O

— I I д д b ^{d e} d t dxdt [ = { F ^ + F } .(38) x^J- h, ^{д£дд                 [}

Используя формулу для ^{~ 2} , нетрудно полу- jk

чить соотношение

I ^F k <

an Thh

< —— h2

(tk ■ + 1 + h 2

IJ

к t k — 1 ^x, + 1 ^— h 2

d² < ( x , t ) d ² < ( x — h , t ) —

dxdt

dxdt

dxdt

+

+ h2

(t_t x ⁺ h '²

J J к tk —1 xj — hl'2

d 11/ (x, t)   d 11/ (x — h, t)

- --

dxdt

dxdt

J

} 12

dxdt

J

,(39)

, j = 2, M — 2, k = 1, N.

Оценим значения

F jk , j = 2, M — 2, k = 1, N .

~ 1

С помощью формулы для F

получим

соотношение

~ 1

F k

_ o/k  1f <1 (xj + hl'2, t)  <1 (xj т , I h

tk

—

^{h 2} , t )

—

t k — 1

к

d x

d x

J

—

1 h ³

f x , + 1 + h ^,;2

x , + h/ '2

x j _{— ]}+ h / 2

Al

< ( x,t ) dx — 2 J <  ( x,t ) dx + J <  ( x , t ) dx > dt

к x j + 1

— h / 2

x j — h 2

x j — 1 ^— hl ²

J

Пусть справедливо равенство

w ) = h

1 ^{f d}< 1 ( x j ⁺ hi '², t )    ^d< l (.

—

xJ— h/2, t)'

—

к

d x

d x

J

—

' ^xj +1⁺ h '²

x j + h '2

x_{j — 1} + hl '2

h ³

к ^xj +1

— I

h 2

x,- hl '2

x j —1 — h '2

J

для фиксированного t e ( 0, T ) . Тогда согласно формуле (40) становится справедливым соотношение

—'1

¹ F jk

tk

= — J P< 1)dt. т /

t k —1

Обозначим

x j

сделаем замену

через x , a x - через £ и

переменных в виде

£ = x — sh . Тогда функционал P ( < ) примет вид

,~,  1 |f < 0,5; I )   < — 0,5; I )

P <  ) =

к d s

ds

0,5

— 0,5

1,5

—

J ~ ( s ; t ) ds +

0,5

+ 2 J ~((s; t) ds — j" ~((s; t) ds ',

— 0,5

— 1,5

где ~ ( s ; I ) = <  ( x + sh; t ) . Очевидно, что P_t (< ) есть линейный функционал относительно < . Кроме того, этот функционал ограничен в пространстве W ₂ ³ ( — 0,5;0,5 ) . Действительно, в силу оценки (11) для фиксированного t e ( 0, T ) функция < ( ^ , t ) принадлежит пространству W ³ ( x — h/ 2; x + h/ 2 ) . Поэтому ~ будет принадлежать пространству W ³ ( — 0,5; 0,5 ) для фиксированного t e ( 0, T ) . Используя (43), получим неравенство

I P< 1 ) <  ^M 9 h "I < 11 W . t e ^{( 0} T ) . (44) где M ₉ >  0 - постоянная, не зависящая от h и т . Кроме того, функционал P_t ( ~ ) обращается в нуль на многочленах второй степе-

ни.

Действительно,

если

возьмем

< = as + bs + c и подставим его для P (~ ), то получим

P Й=

в формулу

h r 1( 2 ^as ^{+ b} )

0,5

— 0,5

—

as3 bs2

—+—+ cs

3

2

к

'   055

J

—

as bs

— + —+ cs

—l

к3

J

—

0,5

1,5

> =

fas3+2l —I---+ cs

bs

3

2J

к

;   0055

—

= -^ { 2 a — 16 ( 0,5 ) 3 a }= ^ { 2 a — 2 a } = 0.

Таким образом, выполнены все условия леммы Брэмбла–Гильберта [1, с.29]. Тогда в силу этой леммы и оценки (44) получим неравенство

| Fs * a 0

i (tk ^x 1 + h ²

(Th)—2  J J

\ t k — 1 ^x 1 ^{— h}l ²

dd( T tH

П22

2       1

d ^ dt

J

I P feh M 9 9 h

- 2 ^d V ~ 1

ds ³

, t e ( 0, T ) .  (46)

L ( — 0,5;0,5 )

Очевидно неравенство

При выполнении обратной замены переменных и возврате к прежним обозначениям согласно (46) получим

^VM дц ²

* M 10

<

^{d 2}V 1 ( - , t ) дц ²

+

L 2 ( 0, l )

^{д 3}V 1 ( - , t ) дц³

L 2 ( 0, l ) J

| F i| * M 10 a 0

₍ t k x j + h /2

\ t k - 1 x j ^— hl ²

^д V дx³

j = 2, M 2, k = 1, N .

2        ²

dxdt

,

V t e [ 0, T ] .

С учетом (51) и (50) получим ³

F 1 k *

J

t _k

1 1     t _k

* M 11 ( T h ^)— 2 h ²   J

Рассмотрим соотношения для F ¹¹ , при

\ tk - 1

\

d 2 V 1 ( : , t ⁾ dr/²

+ (52)

L 2 ( 0, l )

j = 1, k = 1, N. Используя формулу, опреде- ляющую величины F , получим

+

-I t k   x 1 + hj 2

^F"= И J

Th / tk—1 x1—h/2

d и ^{( x} , t )                1

a 0    - 2 dxdt  a 0^xxV1 k dx

^dV G t ) dn ³

A

dt

.

L 2 ( 0, l ) J   J

<   t k x 1 + h/ 2

=Th J J n tk—1x 1— hl2

д V ( x , t ) , , a      ¹ dxdt

⁰    d x ²

—

^— A ^ ¹ k — ^{V 1} k ^{+ V 1} k ^] = h

Используя лемму Брэмбла–Гилберта,

~₁ аналогично неравенству (47) для F  получим

~l *

^M 12 ^a 0 ^h

1 t ^/2

I t k ^x1 ^{+ h} / ²

J J

\ t k — 1 ^x 1 - ^{h 2}

д ³V ( x , t ) dxdt

dxdt

J

,

k = 1, N .

=—   ^й о

Th J ⁰

tk

dv ( x + h/ 2. , t )

—

t k — 1

dx

a ₀ h ²

x 2 + h 2                  h/ 2

V 1 ( x , t ) dx — J v ( x , t k ) dx > dt

. x 2 ^{— h} '²

x — h 2

—

В силу справедливости соотношений (49), (52) и (53) и (48) получим

_л t k ^x 1 ^{+ h 2} t k

.Ml

^T t У _—ldd t V

x + h

d V i A)

t k — 1 x 1 ^— h² t

x

d

d^ — x дщЫd^ ddxd +

Л2 ^д° J

|Fll^ 2 a T ¹² h

a ₀

T3

t k x 1 + h / 2    x       %

MM tk. —1 x1 — h/ 2 x1 — hl 2 x1 — hj 2

d V ( n , t )

। t k   x 2 + h '2

J J

\ t k — 1 ^x 2   ^h! ²

д Vi ( x , t ) д x д t

2       1 ¹²

dxdt

+

j

дц2

d ^ d ^ dxdt =

~1

F 1 k

⁺ F 1 k + F 1 k .

~ 2

Оценим значения F

+

~ 3

и F . Легко ви-

। t k x 1 + h ²

J J

\ t k — 1 ^x 1 ^{— h}l ²

д V i ( x , t ) dxdt

dxdt

J

+

деть справедливость неравенств I F 12I *

t k

⁺ M» ^{t 2} J

\ t k ^— i

^{d 2}V i G t )

dx2

+

L 2 ( 0, l )

^{д V (} ' , t ) дx³

dt

+

L 2 ( 0, l )

J

( tk x 2 + h/ 2

* ² a 0 ^h ^d  J J

\ tk — 1 x 2 ^{— h}/ ²

+

( t k x 1 + h 2

J J

\ tk — 1 ^x 1 ^{— h}l ²

д V 1 (W ) d^dd

d v (W ) дд

d ^ d O

J

+

Xj + h/ 2

1/    t k x ¹ + ^hh

+MTh'i J J

\ t k — 1 ^X 1 ^{— h}/ ²

d V 1 ( x ,t ) dx³

dxdt

J

,

2                '

d ^dO

J

,

k = 1, N .

Аналогично оценке слагаемого   F ₁ ¹ _k ¹

11 оценим величины F :

I F M-1 k\ <  ^{2 a} 0 ^{T 12}h 32

+

( ‘ k X m - 2 + h/ 2

I I

V t k - 1 ^XM - 2 — hl ²

+ M_x т ²

+

( ‘k x M - , + h ²

V ‘k - 1 x M - j ^{- h}l ²

d ² ^ i ( x , t ) d x d t

2 ‘ k

. I

V ‘ k - 1

^d kk ⁽ - , ‘ ) dx³

+ M₁₄a₀т ² h ²

k = 1, N .

d² ^ ( x , t ) ² d x d t

A ¹² dxdt )

d ² ^ i ( x , 11 ) d x ²

dt

J

+

L 2 ( 0, l )

+

‘ k ^xM - 2 ⁺ h ²

I I

V t k - 1 ^XM - 2 - h ²

d ³ ^ 1 ( x , t ) dx³

² 1/2. dxdt

J

+

²       A 12

dxdt

J

Аналогично оценкам (54),(55) и в силу граничных условий для F 1 k ',   F M - 1 _k можно

записать соотношения

I F ‘| <  2 a , r ²² h -³²

+

( t k x 1 + h '2

JI

V t k - 1 x 1 ^- h ²

-1/ V

+ M₁₅a₀т ⁷²h ⁷²

Используя (39),  (47) для F ¹¹ при

j = 2, M - 2, k = 1, N , получим

|j <  ^M 9 ^a 0 ^h^T

( ‘k ^x, ⁺ h ²

V ‘ k - 1 x , ^- h ²

d ³^ 1 dx³

² A dxdt J

+

2 t k ^x i + 11-

1/7/     ¹ k ⁺¹1 '

⁺ а о ^т h I I

( tk ^x + + hi²

+ II

V t k - 1 x j - h 2

।+ h²

V k - 1 j - h ²

d²^ ( x , t )   d²^ ( x - h,t )

dxdt      dxdt

d²^ ( x , t )   d² ^ ( x - h , t )

- dxdt       dxdt

'^

dxdt

J

2      A dxdt J

+

.  (58)

По аналогичной схеме можно получить следующую оценку:

| F kk 11 <  ^M 17 ^a 0 ^h ^ ^т

( ‘ k   x '⁺ h ²

V ‘ k - 1 x , - h ²

д^ 2 dx³

dxdt

J

+

² ‘ k   x ₂ ⁺ h '2

I J

V ‘ k - 1 x 2 - h 2

d² ^ ₂ ( x , t ) ² d x d t

d ² ^ ₂ ( x , t ) d x d t

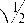
dxdt

J

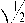
dxdt

J

+

1/-

+ a0 т22 h 72

(t k ^x , + 1 ⁺ h '2

V ‘ k -1 x , + 1 - h 2

^{d 2}V 2 ( ^x , ‘ ) dxdt

d \/ ( x - h , t ) dxdt

A 12 dxdt

J

+

+

+

(‘k x , + ⁺ h ²

V ‘ k - 1 x , ^- hi ²

d ²^₂ ( x , t ) d x d t

—

d ² ^ ₂ ( x - h , t ) d x d t

²       > ^/2

dxdt

J

2 t_k ^x 1 ⁺ h ²

V t k - 1 x 1 - hi ²

|FM- 1 k\ <  ^{2 a} о ^{т 12 h} ’³²

+

d d₂ ( x ,t ) dx³

dxdt

J

k = 1, N .              (56)

( ‘k ^Xm - 1 ⁺ h '²

V ‘ k - 1 ^XM - 1 ^- hl ²

d² ^ ( x , ‘ ) d x d t

2      A 12

dxdt

J

+

( ‘k ^xM - 2 ⁺ h ²

V ‘ k - 1 ^xM - 2 ^{- h}l ²

d² ^ ₂ ( x , ‘ ) d x d t

2      A 12

dxdt J

+

-1/ 1/

+ M₁₆a₀т ⁷²h ⁷²

2 ‘ k x 1 ⁺ h ²

V ‘ k - 1 ^x 1 - h ²

d ³^ ₂ ( x , t ) dx³

2           12

dxdt

J

k = 1, N .               (57)

В силу справедливости неравенств (36), (37), (52), (57), оценок (11), (12) и условия согласования, используя (32), получим соотношение

N M -1     т         /                          \ тhE EIFp I

p = 1,2.            (60)

Из последних неравенств и оценки (31) находим

M -1      т                                       \ h E| zPm\ < M19 V + h + IQ» (vHv II ), j =1

Vm e{1,2,..., N}.         (61)

Выбирая M 6 = M₁₉, получим формулу, доказывающую теорему.

Оценка скорости сходимости разностных аппроксимаций по функционалу

₊1У'^{2 x}j jh²yn) ^hx^j2 ,, L2  d

xj

- h'2 xj-hl 2

A2

dnd^ dxdt S 4h² )

У dx

+

L (7

Оценим разность исходного функционала и дискретной функции.

Теорема 3. Пусть выполнены условия теоремы 2. Тогда для любого v eV и [v]_иeV имеет место оценка

|J(v)- In ^([v]n ) ^ M20 ⁽^ + h+ + I^Qn^(v)- [v]n 11),

+ 4т^{2 У}

dt

.

L2 (a)

Согласно (11) и (67)

J11 S M25 T² + h²).

n = 1, 2,...,

Доказательство. Используя формулу (1) и (13), получим

i J (v)-In^([v ] n n^ M21 (—J j ^y (x, t и* |²dd

V*=1 j=1: ixj - h 2                    ¹        j

+

Суммируя (65) и (66), определяем

(J1 )²SM26T²+ h²+ т + h + Q>,(v)-[v]²). (69)

Аналогично получим следующее соотношение:

(J2f SM27T²+ h²+ т + h + Qn(v)-[v]²). (70)

Неравенства (63) и (70) доказывают

+

^ N M-1 t*

V *=11=1t*-i

^xj⁺h'²                    ₂      A12

j У2(x,t)-ф2*| dxdt xj- hl'2                               ;

= M 22 (J1 + J2 ) ,(63)

Согласно виду формулы, определяющей J , справедливо неравенство

N M-1 t* ^xj⁺h²                   ₂

(J1 )²^²iif  J ^y1 (^x,t)^-yj*| d^dt

*=1 ^j=1 t*-1 Xj- h 2

+

+ 2T, NZ Уj*-Ф1*|² = J11 + J12.    (64)

*=1 j=1

В силу утверждения теоремы 2 получаем

J12 S M 23 T + h + ||e, (v )-[v ] .1Г )•   (65)

теорему.

Сформулируем две вспомогательные леммы.

Лемма 1. Пусть выполнены условия теоремы 3. Пусть, кроме того, оператор Q определяется формулой (23). Тогда Q_n (v) eV и имеет место оценка

IJ (v)-In (Qn (v ))S M28 (It + hh), n = 1,2,.... (71)

Доказательство этой леммы проводится с использованием утверждения теоремы 3.

Пусть оператор P определяется формулой         Pn (^[v^]n ) = ~⁽x),          ⁽⁷²⁾

где

v, + 8-v, (x -x,. - hl21 x,. - hl2 S x S x,. + h/2, j    xj       j           j                 j

Рассмотрим разность y^ - у (x, t). С том соотношения (22) находим 1 xj + h²

~  /У1 (^t* )^d^^-У1^(x,t) =

Xj - h/ 2

Xj + h/ 2

= 7 1(У1 fe )-У1(x ,t))d^ = h - J h/ 2

v (x )=<

уче-

v₁

j = 2,M -1, (73) x - h/ 2 S x S x + h/ 2 .

Лемма 2. Пусть выполнены условия теоремы 3. Пусть, кроме того, оператор P определяется формулой (72).    Тогда

P([v]„) e V и имеет место оценка

IJ (Pn ([v ] n))-In ([v 1,) S M 29 ((Гт + hh ),

, xj⁺h² Pt*

=1J J n x} - h/2 L t

tk

j

^y (^’     d (n, t)

d0 + d0     { dn

n = 1,2,....           (74)

С учетом (66) получим

N M -1 t* ^xj⁺h²^ 1 ^xj⁺h²t*

J11S 2Ш J 1 M

*=1 j=1 t*-1 Xj-h2 V 7,.-hl2 t*-

xj^-h²h-1

dn d^.(66)

dy. (^, 0}

Ц   7 d0d^ + d0

Доказательство. Нетрудно установить, что P I[v]   eV.

nn

Поэтому в записи теоремы 3, выбирая ~(x) = P_n([v]_n) вместо v и проводя анало-

гичное доказательство, получим оценку

| J (Pn ([v ] n ))-In ([v ] n ) < M30 (^ + h+ +1Qn (~)-[v] n| I),

n = 1,2,....               (75)

Легко видеть, что

,      M -1,          „      M -1 1 xj+h^{2              2}

I Qn(~)-[ v] nil = h II wj—v\ = h I?.[ ~(x) dx —vj = j=1                   j=1 h xj - h 2

M-1 1 xj+ h'2           .          M-1 1 xj+ h⁷

=hI,  •■x)-vid =hI , I j=1 hxj - hl2                      J=2 hxj - hl2

‘I

‘I

•

M-1

=hI j=2

8-v xj

h

xj + h²

|(x - xt - h2)dx xj- h2

m -18 v 1

=h If(x- xj

-

h2)2

xj + h'2

x_} - h'2

M-1

=hI j=2

8v, • h2

xj

2h

m-18 v      m-1L2

=hY^h ^hYb-h i=7   2          /=7 4

M-■ 8 v

Отсюда получим

II Qn (v~)-[v ] .1 s lb-hh-

lb12h2

.

Это неравенство и соотношение (75) доказывают лемму.

Сформулируем и докажем теорему о скорости сходимости разностных аппроксимаций по функционалу.

Теорема 4. Пусть выполнены условия леммы 1 и 2. Пусть, кроме того, v eV и [v]_neV_n являются решениями задач (1)-(5) и (13)–(17) соответственно, т. е.

J* = inf J (v ) = J (v ‘ ) In * = [inf In ([v] n ) = In ([v]n ).

^{veV                               [}v ]n ^eVn

Тогда последовательность разностных задач (13)–(17) аппроксимирует задачу (1)– (5), т.е.

lim In * = J*              (76)

n 4»

и справедлива оценка о скорости сходимости:

I In * - J* I < M 31 (xT + hh ), n = 1,2,.. ..(77)

Доказательство этой теоремы проводится с использованием леммы 1 и 2.