Об одной численно-аналитической схеме расчета первых моментных функций вектора состояния линейной стохастической интегро-дифференциальной системы

Модели в форме детерминированных и стохастических интегро-дифференциальных уравнений (ИДУ, СИДУ), обыкновенных и в частных производных, интересны как с теоретической, так и практической точек зрения вследствие того, что эти уравнения описывают значительное число явлений в различных областях, в частности, в теории колебаний с учетом аэроавтоупругости [1], наследственности материала [2], вязкоупругости [3] и др. Общая теория и первичная классификация детерминированных интегро-дифференциальных уравнений была разработана Вито Вольтерра [4] в первой

Работа выполнена при частичной финансовой поддержке Минобразования и пауки России (Задание № 2014/153).

половине XX в. Некоторые современные общие приложения ИДУ рассмотрены в [5].

Системы обыкновенных СИДУ, например в стохастической механике, часто возникают как результат применения таких методов, как метод конечных элементов (МКЭ) [6], метод конечных разностей (МКР) [7], метод Галеркина [8], метод прямых [9], разложение неизвестных функций по собственным функциям краевой задачи [10, 11] или каким-либо специальным функциям [12], к СИДУ в частных производных (СИДУв-ЧП) [13], которые описывают непрерывные вязкоупругие среды. После преобразования ИДУвЧП или СИДУвЧП в обыкновенные ИДУ или СИДУ зависящая от времени структура ядер в обыкновенных детерминированных или стохастических интегро-дифференциальных уравнениях движения сохраняется.

От некоторых таких уравнений (как пра- вило, это случаи вырожденности ядер [11, 14, 15]) возможен переход к дифференциальным уравнениям с помощью расширения пространства состояния. Однако существуют эволюционные ИДУ, служащие моделями во многих областях науки и содержащие интегрирование по времени, для которых это сделать сложно. Такие уравнения [4], обыкновенные и в частных производных, описывают сложное поведение объектов в различных средах с учетом предыдущей истории, температуры и других факторов [16-20].

Нелинейные и линейные стохастические ИДУ, кроме предыстории, позволяют учесть влияние на поведение объекта случайных возмущений. Достаточно общие формы линейных систем СИДУ имеют следующий вид:

x ( t ) =

A(t) X (t)+ ( t0

B( t, t ) X ( t ) dT +

+ c (t ) + G( t ) V (t ) ,    X (t о) = X о . (0.1)

В этих уравнениях t - время, t E T = [ t о ,T ], T <  + от:

X ( t ) = col( X i( t ) ,X 2 ( t ) ,...,X n ( t ))

И

V ( t ) =col( V _L( t) ,V 2 ( t ) ,...,V m (t ))

• -    случайные векторные процессы, определяющие состояние системы (вектор состояния) и случайные возмущения;

c ( t ) = col ( с 1( t ) ,c 2( t ) , . . .,C n (t )) ,

A( t ) = {a ij ( t ) } E M nxn , B( t,T ) = {b ij ( t,T ) }EM n _X n

(bij ( t,T ) ^ 0 для всех T. t E T).

^G( t ) = ^{g ij ⁽ t ) ^{} E} M nxm

• -    неслучайные вектор и матрицы, компоненты которых дифференцируемы необходимое число раз по каждому из своих аргументов; X о - случайный вектор с известными характеристиками, причем вектор V ( t ) статистически независим от X о; R s - стандартное евклидово пространство размерности s, R = ( —от, + от ): col dd _L ,d2,...,ds) - вектор-столбец с соответствующими компонентами;

M _{s x} q ^ множество действительных матриц размерности s х q-, точкой или точками сверху символа обозначаются производные по переменной t соответствующего порядка.

Вопросы связанные с определением СИДУ, существованием и единственностью их решений представлены в [21,22]. Общие идеи стохастической динамики были рассмотрены в [12,23,24].

Хорошо известно (см., например, [25] и там историю развития методов численного анализа), что решение интегро-дифференциальных уравнений является очень сложной проблемой даже в детерминированном случае. Этих трудностей еще больше при анализе линейных и нелинейных стохастических задач. Несмотря на существование ряда результатов, касающихся алгоритмов для стохастических интегро-дифференциальных уравнений (см., например, [13]), очень полезно адаптировать существующие методы решения детерминированных ИДУ для стохастических случаев, потому что основная часть методов качественного и количественного анализа явлений, описываемых ИДУ, состоит из детерминированных схем.

Ранее был разработан ряд схем для построения численных приближений решений детерминированных и стохастических интегро-дифференциальных уравнений. Что касается рассмотрения стохастических задач, приближенные алгоритмы обычно используются для прямого расчета поведения систем во времени. Эти схемы включают:

• -    полностью численные методы (классические и модифицированные гибридные), такие как явные и неявные схемы Эйлера [25] и МКЭ [26] для ИДУвЧП, Тан-метод [27], одношаговые и многошаговые методы Рунге-Кутты [28-31] для ИДУ, одношаговые методы Рунге-Кутты 4-го порядка [32], метод Рунге-Кутты [33] для расчета ковариационными функций, методы экстраполяции [34], Галеркина [35], итераций на последнем шаге [1], использование вейвлетов [36], определенных глобально Sinc-базисных функций [37], приближенное преобразование ИДУвЧП в ДУвЧП и СИДУ в СДУ на основе усреднения ядра [13,38-40];

• -    приближенные аналитические методы, в т.ч. методы рядов Тейлора [41], после-

• довательных приближений для вычисления функции Грина [42], асимптотический метод [43,44] для ИДУ и метод стохастического усреднения для СИДУ [2,45], методы многих масштабов [46], коллокации [47], теории возмущений [48], неподвижной точки на основе биортогоналвных систем для банаховвк пространств [49].

Заметим, что существует ряд прибли-женнв1х схем для упрощения интегральных ядер, такие как использование рядов Про-ни и алгоритм аппроксимации полиномами Лагерра для представления функций релаксации [50], метод приближения переходных функций экспонентами [1], приближенный вывод уравнения Фоккера-Планка-Колмогорова для СИДУ [51], расширения фазового пространства для случая ограниченности носителя ядра [52] и т.д. Основная цель таких упрощений - получить вырожденные в том или ином смысле ядра, что позволяет на основе расширения пространства состояния привести исходные СИДУ к системе стохастических дифференциальных уравнений (СДУ). Методика, представленная в настоящей работе, предназначена для анализа линейных динамических систем, описываемых стохастическими интегро-дифференциальными уравнениями, созвучна идеям алгоритмов данного направления, близка к схемам, изложенным в работах [15,53], и базируется на локальной аппроксимации ядер СИДУ, что позволяет построить цепочку замкнутых обыкновенных дифференциальных уравнений для вычисления первых моментных функций вектора состояния системы.

1.    Постановка задачи

Пусть X о - гауссов случайный вектор со значениями в R n.

m x о = Е [ X о ] ,

D x о x о = Е [ { X о - m x о ^}{ X о — m x о ^}Т ] ;

V(t) - случайный процесс, удовлетворяющий векторному линейному СДУ Ито dV (t) = H V (t) dt + Q dW (t),(1.1)

t € (tо,T](1.2)

co случайным начальным условием

V (t о) = V о.(1.3)

В уравнении (1.1)

^H = ^{h ij ^{} €} ^M mxm

И

Q = {q ij } € M m^r

• -    заданные постоянные матрицы;

W ( t ) = col( W 1 ( t ) , W 2 ( t ) ,..., W r ( t ))

• -    векторный винеровский случайный процесс с независимыми компонентами, такой, что его обобщенная производная по времени t, обозначаемая через

W(t) = col(WДt), W2(t),..., Wr(t)) , есть векторный гауссовский белый шум с независимыми компонентами,

Е [ W (t )] =0 ,

Е WV tt ) W ^Т ( t ' )] =2 п E r 5 ( t - t ' );

6 - дельта-фушщия Дирака: T - символ транспонирования; Es - единичная матрица порядка s; Vо - начальный вектор, представляющий собой центрированную гауссову случайную величину со значениями в Rm. Предполагается, что плотность вероятности вектора Vо - гауссово стационарное распределение, ассоциированное с уравнением (1.1). Параметрами этого распределения являются среднее myо = Е[Vо] = 0 и матрица дисперсий Dуоуо = Е [Vо (Vо)т]. Кроме того, в уравнении (1.1) матрицы H и Q таковы, что V - случайный процесс второго порядка. Следовательно, {V(t),t € [tо,T]} - стационарный центрированный непрерывный в среднем квадратическом гауссовский случайный процесс, для которого my (t) = Е [ V (t)] = myо = 0,

C УУ ⁽ t 1 ,t 2 ) = ^Е [ ^{V (} t 1 ) ^{V Т (} t 2 )] = C УУ ⁽ t 1 ^— t 2 ) , D УУ ⁽ t ) = D УУ = C УУ ⁽⁰⁾ = C У о У о .

Учитывая, что X о 11 V - гауссовские случайные вектор и процесс соответственно, линейность уравнений (0.1) и (1.1), а также высказанные выше предположения, можно установить, что { X ( t ) ,t € [ t о ,T ] }

- непрерывный в среднем квадратическом гауссовский случайный процесс второго порядка. При этом для всех непуств1х и неупорядоченных точечных подмножеств отрезка [ t о ,T ] многомерные распределения расширенных случайных векторов состояния будут гауссовыми, определяемыми соответствующими векторами средних и матрицами ковариационнв1х функций.

Определим теперв векторную функцию математического ожидания, матрицы ковариационных функций и дисперсий векторного случайного процесса X ( t ), а также все взаимные ковариационные функции X ( t ) с вектором возмущения V ( t ):

m x ( t ) = £ [ X ( t )] ,

C xx ⁽ t 1 ,t 2 ) = ^£ [ X ⁽ t 1 ) X ^{T (} t 2 )] ^—

- m x ( 1 1 ) m X ( 1 2 ) ,

D xx ( t ) = C xx ( t,t ) ,

C xv ( 1 1 ,t 2 ) = £ [ X ( 1 1 ) V ^T ( 1 2 )] , C vx ( 1 1 ,t 2 ) = £ [ V ( 1 1 ) X ^T ( 1 2 )] .

Принимая во внимание введенные определения и обозначения, несложно увидеть, что решение поставленной задачи заключается в создании схемы для вычисления векторной функции математического ожидания m x ( t ) ^и матрицы ковариационных функций C xx ( 1 1 , t 2 ) ДЛЯ Лтобых t,t 1 ,t 2 G ( 1 0 ,T ].

Введенный случайный процесс Y ( t ) будет удовлетворять системе СИДУ

d Y ( t ) = {A( t ) Y ( t ) +

+

f t '

^{B( t,T} ) ^{Y ( T} )

dT + c ( t )} dt +

(2.3)

+ Q d W ( t ) , 1 0 <  t ' <  T

co случайным начальным условием

Y ( t ' ) = Y ' ,

Y ' = col( X о , V 0 ) дтя t ' = 1 0 .

В уравнении (2.3) матрицы

^A( t ) G .^4 ( n + m ) x ( n + m ) , ^B( t ) ^G M. ( n + m ) _x ( n + m ) , G⁽ t ) ^G M. ( n + m ) xm ,

Q GM ( n ₊ m ) xr

и вектор c (t) G Rn+m

(2.4)

имеют блочную структуру и определяются

так:

B( t ) =

B( t ) O mxn

G( t )

A( t )   G( t )

O mxn ^H

O nxm

O mxm

G( t )

mxm

]■ c ( t ч c m \

Q

O nxr

Q

2. Методика решения задачи

Для получения требуемых уравнений необходимо расширить вектор состояния системы (0.1) до нового случайного вектора Y ( t ) = col( X ( t ) , V ( t )) co значениями в r n + m т_0Гд_а вектор-функция математичес кого ожидания m Y ( t ) co 'значениями в R n ^{+ m} и матрица ковариационных функций C YY ⁽ t 1 ,t 2 ) ^G ■^d ( n + m ) x ( n + m ) с ян чайного про цесса Y ( t ) определятся соотношениями

где O _sX q и 0 _s — нулевые матрица и вектор размерностей s х q н s соответственно.

Введем временную сетку

1 ₀ = 1 ₀ 1 < ... < t k- 1 k< ... < t_N = T, h k = t k - t k- 1 , k = 1 , 2 ,...,N, max h k = h * ^ 1 ,

k

m Y ( t )=[ m xt^

C xx ⁽ t 1 ,2 2 ) C xv ⁽ t 1 ,2 2 )

C YY ⁽ t 1 ,2 2 ) =                                       .

C Vx ⁽ t 1 ,2 2 ) C VV ⁽ t 1 ,t 2 )

(2.2)

так, чтобы матричное ядро B( t, t ) на отрезке △ k = [ t k- 1 ,t k ]. k ^ 1c достаточной точно стью можно было заменить на

L вk(t,T) = J2Bki(t) (T - tk-1 /2)l, i=0

где_ в m 1 d 1 B(t,T)

Bki (t) = I!    dT1’

^T = t k- 1 / 2

,      _ tk-1 + tk tk-1 / 2 = -----5

Тогда для отрезка A k аппроксимацию системы (2.3) с начальным условием (2.4) можно записать так:

d Y k ( t ) = {A( t ) Y k ( t ) +

+

It B k ( t,T )

^tk- 1

Y k ( т ) dT + c (t )} dt +

+ Q d W (t),  t k- 1 <  t k , (2.5)

Y k ( t k- 1 ) = Y k- 1 ( t k- 1 ) .       (2.6)

Введем новые неизвестные случайные вектор-фуикции { Z ы ( t ) , £ — 0 ,L, t G A k } c помощью соотношения

Z kc ( t )- t k ( т - t k- 1 / 2 ) ^C X k ( т ) dT.

Тогда система СДУ для векторного случай ного пропосса S k ( t ) — col ( Y k ( t ) , Z kc ( t ) , £ —

0 ,L, t G A k) будет иметь вид:

dSk (t) - [Ak (t) Sk (t) + ck (t)] dt+ и матрицы дисперсий

Ds _k s k ( t )- A k ( t ) Ds k s k ( t ) +

+ [ A k ( t ) Ds k s k ( t )] ^T +2 n Q k QJ (2.11) расширенного вектора состояния на промежутке A k- Начальными условиями для указанных векторных и матричных функций будут:

^m s k ⁽ t k- 1) ^{- m} s k- 1 ⁽ t k- 1) ’       (2.12)

Cs k s. k ( T,T )- Ds k s k ( T ) ,         (2.13)

Ds k s k ( t k- 1 )- Ds k- is k- 1 ( t k- 1 ) .     (2.14)

Итак, последовательно решая уравнения (2.9)-(2.11) с начальными условиями (2.12)(2.14), мы получим характеристики случайного векторного процесса S( t ) на сегментах A1, A1, ..., A n. По построению искомые характеристики процесса X ( t ) представляют собой первые блоки вектора m s( t ) и матриц Css( t,T ) 11 Dss( t ) размер постен n и n x n соответственно.

где

+ Q k d W ( t ) ,

^S k ⁽ t k- 1 )   ^ k— 1 ⁽ t k- 1 ) ,

A k ( t ) - Г

A ( t )

A k ¹²( t )

A k ^21]( t )   A k ^22]( t )

,

----

.—-

(2.7)

(2.8)

A k ^12]( t ) =

B k o ( t )    ... B kL ( t )

O mxn

E n

.

.

.

A k ^21]( t ) =

⁽ t ^— t k- 1 / 2 ) E n

...

O mxn

O nxm :  O nxm

...

,

,

⁽ t ^— t k- 1 / 2 ) L E n

O nxm

A_k ( t ) = O n ( L +1) xn ( L +1) ,

C ‘ ⁽ t ’=[ O c ⁽ t ’ 1 ’ ° k =[

⁰ n ( L +1)

Q

O n ( L +1) xr

.

Используя уравнения (2.7), (2.8) и соотношения из [54, §1.3], можно получить системы ОДУ для вектора математических ожиданий

—

3. Пример

Исследуем переходный процесс, описываемый модельным уравнением

U( t ) + 2 aU( t ) + ш ² U ( t )+

t

+ в J e-Y(t-T)2 U( т) dT - ^V (t), ('CC U (0)-0 U0, 17(0)- 170, где a > 0. ш > 0. в- Y > 0- Ц - постоянные величины.

Если обозначить U ( t ) не]тез X 1( t ). a U ( t ) - через X 2( t ) ( n - 2), то, приводя уравнение (3.1) к виду (0.1), получим

^A( t ^)- [ -Ш 2 - ¹ a ] ’ c < t ^)- [ ⁰ ] ’ » <М^)- [    .^'( t-T ) ’ ⁰ ] ’ G t ^)- [ ’ ] •

Будем считать, что процесс V ( t ) удовлетворяет уравнению

^m s k ⁽ t ) = A k ⁽ t ) ^m s k ⁽ t ^{) + c} k ⁽ t ) , матрицы ковариационных функций

(2.9)

dV ( t )- -hV ( t ) dt + qdW ( t ) , h> 0 (3.2)

d Cs _k s _k ( t,T ) ∂t

^— A k ⁽ t ) Cs k s k ⁽ t’ ^T ) ’

(m - r - 1), а следовательно, спектральная плотность и дисперсия процесса V ( t ) будут соответственно равны

t k- 1 Ф T < tk, (2.10)

q ²

S VV ^{( Ш} ) ш ² + h ² ’

Dvv - nq-. h

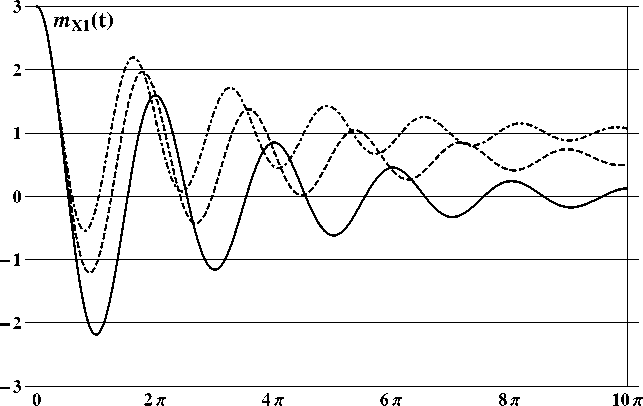
Рис.1

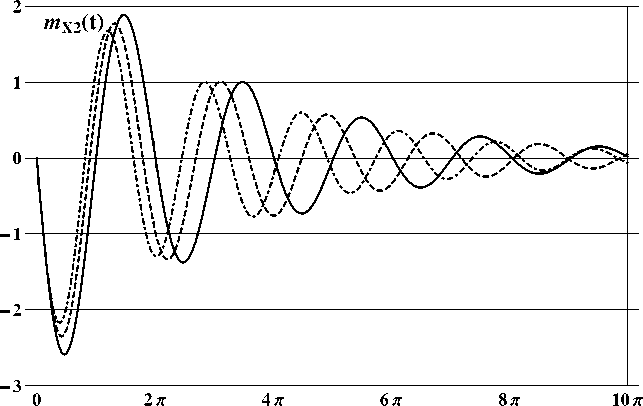
Рис.2

Результаты расчетов математических ожиданий и элементов матрицы дисперсий, проводившихся с помощью программы на входном языке пакета Mathematica [55], для следующих значений параметров:

α =0 . 1 ,β =0 . 2 ,γ =0 . 125 ,

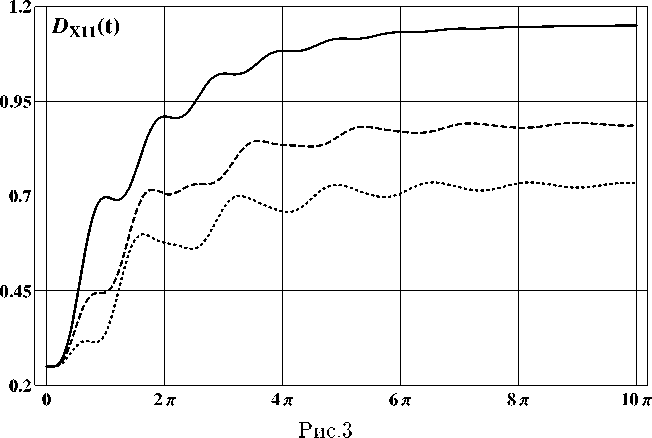
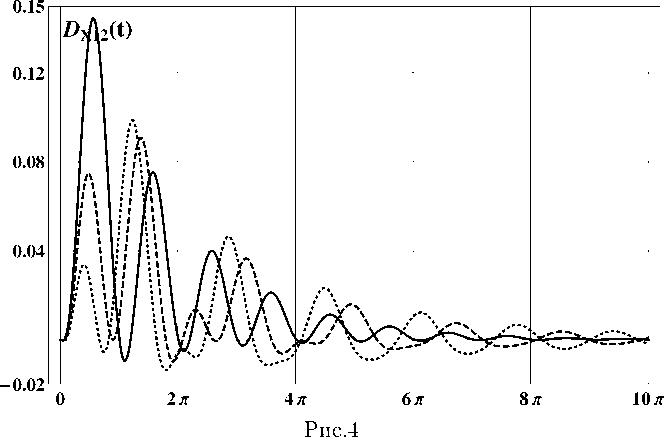
μ =1 . 0 ,T =10 . 0 π, L =4 ,ω =1 . 0 , h =2 . 0 ,q =0 . 6 ,h∗ = h k = 0 . 005 π, m X (0) = col(3 . 0 , 0 . 0) , D XX (0) = diag(0 . 25 , 0 . 25) отображены на рис. 1 (mx 1(t )); рис. 2 (mx 2( t )): рп<•- 3 (D_X 11( t )): pile. 4 (D_X 12( t )):

puc. 5 ( D x 22 ( t )) при в = 0 . 0- 0 . 25 ¹¹ 0 • 5 непрерывными, штриховыми и штрих-пунктирными линиями соответственно.

Анализ приведенных рисунков показывает, что интегральный член играет роль добавочного демпфирования, а его величина существенно влияет на величины частот колебаний и смещений равновесных значений математических ожиданий и элементов матрицы дисперсий.

Заключение

Рассмотренную в настоящей статье проЦеДУРУ можно отнести к схемам как расши-

рения пространства состояния, так и анализа систем с изменяющейся структурой, причем если расширение такого пространства осуществляется единожды на этапе выбора точности аппроксимации ~ O ((0 . 5 h * ) L ) матричного ядра системы, то изменение структуры (уравнений) происходит на каждом из сегментов A k- k = 1 , 2 , ...,N. причем для ре шения ОДУ для математических ожиданий и элементов матрицы дисперсий на этих сегментах применимы стандартные численные интеграторы.

Используемое в данной работе тейлоровское разложение матричного ядра системы возможно только при наличии достаточного числа двусторонних производных у этого ядра внутри сегментов Ak и односторонних на его концах. В случае слабосингулярных ядер, которые нередко используются в моделях вязкоупругости, рассмотренный алгоритм непригоден. Для анализа уравнений с подобными ядрами необходимо обращение к специализированным схемам [56].