Об одном методе решения задачи идентификации динамических систем

Известным подходом к решению задач параметрической идентификации динамических систем является сведение к задачам оптимизации параметров. Для решения возникающих задач, как правило, применяют методы конечномерной оптимизации неявно заданных целевых функций. Менее распространенным подходом является интерпретация задачи идентификации как задачи оптимального управления и применение аппарата теории и методов оптимального управления для поиска оптимальных параметров. При этом используют методы, основанные на реализации необходимых условий оптимальности управления [1] и локальные методы улучшения управления, в частности градиентные [2].

Предлагаемый в статье метод является модификацией развиваемых нелокальных методов улучшения и оптимизации управлений на основе решения конструируемых задач о неподвижной точке в пространстве управлений [3; 4] применительно к рассматриваемой задаче идентификации. Эти методы являются развитием нелокальных методов, которые были первоначально разработаны в классах линейных [5] и полиномиальных [6] по состоянию динамических систем и основывались на решении специальных задач Коши и краевых задач в пространстве состояний.

• 1    Задача идентификации

Задача идентификации динамических систем рассматривается в следующей постановке аналогично работам [1; 2].

Пусть измеряются выходные характеристики динамического объекта y ( t ) = ( У 1 ( t ),—, У, ( t )) на фиксированном интервале времени T = [ t ₀, t j. Относительно объекта известна дифференциальная система уравнений движения:

x( t ) = f ( x ( t ), о , t ), x ( t o ) = a , o e W , a e A , (1) в которой x ( t ) = ( x , ( t ),..., x_n ( t )) — вектор состояния, о = ( ® 1 ,..., to m ) и a = ( a^...,a n ) — векторы параметров. Множества W c R^l , A c Rⁿ выпуклы и замкнуты.

Ставится задача определить вектор параметров с = ( о , a ) со значениями в множестве Q = W х A , при котором заданная функция Ф ( с ) от параметров, характеризующая меру близости решений системы (1) x ( t ) = x ( t, с ), t e T к функции y ( t ) = ( y 1 ( t ),..., y_s ( t )), t e T , принимала наименьшее значение:

Ф ( о ) = [ F ( x ( t ), y ( t )) dt = [ F ( x ( t ), t ) dt ^ inf .        (2)

T

T

σ ∈ Ω

n

^{F ( x} , У ) = Е ^{X (} x - У ‘ ^).

i = 1

Отметим актуальный для приложений случай, в котором задача идентификации (1), (2) находит важное применение.

При моделировании многих задач математической физики возникает проблема поиска их решений, обусловленная большой размерностью и сложностью моделируемых систем дифференциальных уравнений. Известным подходом к исследованию таких задач является упрощение модели, сводящееся к замене исходных дифференциальных уравнений более простыми уравнениями меньшей размерности. Задачу упрощения и понижения размерности системы дифференциальных уравнений можно сформулировать в следующей постановке аналогично работам [1; 2].

По известной выходной характеристике y ( t ) = ( y ₁( t ),..., y_s ( t )) заданной системы дифференциальных уравнений:

^{y (} t ) = ^{7 (} У ⁽ t X t ), У ⁽ t 0 ) = У ⁰

требуется определить параметры системы (1) при n <  s , для которой заданная функция (2), характеризующая близость решений систем, принимает наименьшее значение.

Таким образом, задачу упрощения и понижения размерности дифференциальной системы можно рассматривать как частный случай задачи идентификации (1), (2).

• 2    Метод неподвижных точек

Задача (1), (2) рассматривается как задача оптимального управления при следующих предположениях.

Функции f ( x , о , t ), F ( x , t ) и их частные производные по переменным x и ω непрерывны по совокупности аргументов на соответствующих множествах Rⁿ х W х T и Rⁿ х T . Функция f ( x , о , t ) удовлетворяет условию Липшица по x в Rⁿ х W х T с константой L >  0: II ^{7 ( x} , ^о , t ) ^{- 7 (} У , ^о , t )|| <  L ||x ^- У 11 .

Условия гарантируют существование и единственность решения x ( t , < 7 ), t е T системы (1) для любого допустимого управления о еО .

Функция Понтрягина с сопряженной переменной ψ ∈ Rⁿ и стандартная сопряженная система в задаче (1), (2) принимают следующий вид:

H ( ^ , x , о , t ) = ( ^ , 7 ( x , о , t )) - F ( x , t ),

• Ч & ( t ) = — H x ( V ( t ), x ( t ), о , t ), t е T , ^ ( t i ) = 0.          (3)

Для допустимого управления о eQ обозначим ^ ( t , о ), t е T - решение стандартной сопряженной системы (3) при x ( t ) = x ( t, о ) и аргументе to , соответствующему вектору о . Обозначим частное приращение произвольной вектор-функции g ( y_x,..,y_t ) по переменным y s , y_s :

^А ys , ^+А ys , . ys 2 ^+A ys 2 ^{g (} y ¹ ’"'’ y ) =

= g ⁽ y i ,-, y s , ^+A y s , ,-, y s ₂ ^+A y s ₂ ,-, yi ) ^- g ⁽ y i ,-, yi )

Рассмотрим задачу улучшения управления в следующей общей постановке:

для заданного управления σ ^I ∈ Ω требуется найти управление σ ∈ Ω с условием А _о Ф ( о ⁷ ) = Ф ( о ) - Ф ( о ⁷ ) <  0 .

В соответствии с работой [4] определим модифицированную дифференциально-алгебраическую сопряженную систему в форме:

p ⁽ t ) = ^- H x⁽ P ⁽ t ), x ⁽ t ), ^to , t ) ^- r ⁽ t ), P ⁽ t l ) = ⁰,                   ⁽⁴⁾

(Hx ⁽ P ⁽ t )> x ⁽ t )> ^to - t ) ⁺ r ⁽ t )> y ⁽ t ) — x ⁽ t )) = ^A y ( t ) H ⁽ P ⁽ t )> x ⁽ t )> ^to - t ) ,      ⁽⁵⁾

в которой по определению полагаем r ( t ) = 0 в случае линейности функций F , f по x (линейная по состоянию задача (1), (2)), а также в случае y ( t ) = x ( t ) при соответствующих t е T .

В линейной по состоянию задаче (1), (2) модифицированная сопряженная система (4), (5) в силу определения совпадает со стандартной сопряженной системой (3).

В нелинейной по состоянию задаче (1), (2) алгебраическое уравнение (5) всегда можно разрешить относительно величины r ( t ) (возможно, не единственным образом).

Для допустимых управлений о eQ , о ⁷ eQ обозначим p ( t , о ⁷ , о ), t е T — решение модифицированной сопряженной системы (4), (5) при x ( t ) = x ( t , о ⁷ ), y ( t ) = x ( t, о ), to = to ⁷ . Из определения следует очевидное равенство p ( t , о , о ) = у (t, о ), t е T .

Обозначим P Y — оператор проектирования на множество Y с R k в евклидовой норме

P y ( z ) = arg min(|| y - z ||), z e R k .

y ∈ Y

Из работы [4] следует, что для решения задачи улучшения заданного управления σ ^I ∈ Ω достаточно решить следующую систему уравнений относительно о = ( to , a ) при заданном параметре a >  0:

to = P w ( to¹ + a j H to ( p ( t , о ⁷ , о ), x ( t, о ), to ⁷ , t ) dt + s ^to ),                (6)

T

А ю f H ( Р ( t , ° , ° ), x ( t , ° ), ю¹ , t ) dt =

T

/                                                      \             (7)

= И H _m ( p ( t , ° , ° ), x ( t, ° ), ю¹ , t ) dt + s " , ю - ю

T a = Pa(a1 + ap(10,°,°)),                     (8)

в которой в уравнении (7) по определению полагается s ™ = 0 в случае линейности функции f по ю (линейная по параметру ю задача (1), (2)), а также для ю = ю ¹ .

В нелинейной по параметру ю задаче (1), (2) уравнение (7) всегда можно разрешить относительно величины s ^ю (возможно, не единственным образом).

Таким образом, систему (6)-(8) всегда можно свести (возможно, не единственным образом) к приведенной системе уравнений с однозначно определенной величиной s ^ю .

Пусть система условий (6)-(8) имеет решение ° ^п = ( ю ¹¹ , a¹¹ ) (возможно, не единственное). Тогда имеет место оценка улучшения целевой функции:

А °" ф(°1) < - 0a р—ю । f - a aa11—a1112.

В частном случае задачи (1), (2), когда вектор начальных условий a е A не меняется и имеет заданное значение, задача улучшения управления сводится к системе уравнений (6), (7).

Структура полученных условий улучшения управления и используемая система обозначений решений фазовой и сопряженной систем в форме явной зависимости от управления позволяет интерпретировать систему уравнений (6)-(8) как задачу о неподвижной точке специального оператора управления. Это позволяет применить развитую теорию и методы неподвижных точек для эффективного поиска улучшающих управлений.

Выбирая однозначно определенные правила определения указанных выше величин r ( t ) и s ^ю , будем получать однозначно определенные операторы управления. Таким образом, возникают модификации предлагаемого метода неподвижных точек для улучшения управления с различными однозначно определенными операторами управления. Множества неподвижных точек возможных модификаций оператора управления позволяют сущест -венно расширить потенциал улучшения заданного управления.

Данная особенность предлагаемого подхода неподвижных точек позволяет конструировать специальные вычислительные технологии улучшения управления, в которых на каждой итерации улучшения выбирается наилучшее по определенному правилу управление. Такие технологии улучшения управления могут эффективно реализовываться с помощью параллельных вычислений на многопроцессорных компьютерах.

Выделим другую важную особенность предлагаемого метода.

Решение CT ¹ eQ задачи о неподвижной точке, отличающееся от улучшаемого управления ст ¹ eQ , обеспечивает строгое улучшение по целевой функции ввиду указанной ранее оценки улучшения. Это свойство позволяет методу неподвижных точек строго улучшать экстремальные неоптимальные управления ст ¹ eQ , удовлетворяющие дифференциальному принципу максимума [1] в задаче (1), (2), в случае существования неподвижных точек, отличающихся от ст ¹ eQ .

Метод решения задачи идентификации состоит в последовательном решении конструируемых задач о неподвижной точке для улучшения управления.

• 3    Итерационный алгоритм решения

Для численного решения задачи о неподвижной точке (6)-(8) для улучшения заданного управления ст ¹ выбирается следующий итерационный процесс при k >  0 :

CT ^{+ 1} = P w ( CT + a j H _m ( p ( t , CT , CT ), x ( t , CT ), CT , t ) dt + s ^m ),

T

A _to k j H ( p ( t , CT , CT ), x ( t , CT ), CT , t ) dt = T

, jHm(p(t,CT,CT),x(t,CT), CT,t)dt + sto,CT - CT \ T ak+1' = Pa(a1 + ap(to,CT,CT)).

Задается начальное приближение итерационного процесса ст ⁰ eQ при k = 0.

Расчет задачи о неподвижной точке (6)-(8) осуществляется до первого улучшения исходного управления CT . Далее строится новая задача улучшения для полученного управления CT I , и расчет повторяется. Итерации улучшения управления продолжаются до тех пор, пока не выполнится условие

| Ф ( ст ") -Ф ( ст ¹ )| <  8 ф ( ст ¹ )| , где 8 >  0 — заданная точность расчета.

Анализ принципиальной сходимости рассматриваемого итерационного процесса к решению задачи о неподвижной точке при достаточно малых параметрах проектирования a >  0 проводится аналогично работам [4; 6] на основе известного принципа сжимающих отображений, применяемого в работе [7].

Предлагаемый метод неподвижных точек характеризуется тем, что улучшающие управления определяются решениями соответствующих задач о неподвижной точке при любом значении параметра проектирования a > 0. В частности, при достаточно малых a > 0, обеспечивающих принципиальную сходимость конструируемого итерационного процесса последовательных приближений к решению задачи о неподвижной точке.

В целом, оптимизация управлений на основе расчета конструируемых задач о неподвижной точке предлагаемым итерационным методом последовательных приближений сводится к чередующемуся решению задач Коши для фазовых и сопряженных переменных.

Эффективность предлагаемого алгоритма решения задачи идентификации иллюстрируется на расчете модельной задачи упрощения и понижения размерности дифференциальной системы уравнений.

• 4    Модельная задача «Кинетика ядерного реактора»

Рассматривается задача понижения размерности системы дифференци альных уравнений, описывающей кинетику ядерного реактора [1]: у, = 641,02у + 21,02 у 2 +141,03 у3 +120,192у 4 + +253,844у5 + 74,358у6 + 27,051у7 + 200,

у ₂ = 0,0123 ( у ₁ - у 2 ) , у з = 0,03 ( у ₁ - у 3 ) , & 4 = 0,112 ( у ₁ - у 4 ) , у = 0,301 ( у 1 - у 5 ) , у 6 = 1,149 ( у - у 6 ) , у 7 = 3,012 ( у - у 7 ) , у 1 (0) = ... = у 7 (0) = 0,25, T = [0,8].

Идентифицируемая упрощенная система имеет вид: x = w 1 x + w ₂ x ₂ + w ₃, x ₂ = w ₄ x 1 + w ₅ x 2 , X 1 (0) = v_p x 2 (0) = v 2 , T = [0,8].

В качестве минимизируемой целевой функции, характеризующей близость решений, рассматривается среднеквадратическая ошибка:

• 8 2                        ₂

I ⁽ w^v ) = JE ( x ⁽ t ) ^- у - ⁽ t ) )² dt , ^w = ( w 1 ’-> ^w 5 ) , ^v = ( ^v 1 , ^v 2 ) .      ⁽¹¹⁾

0 - = 1

Задача состоит в определении таких значений вектора параметров (w, v), при которых целевая функция (11) принимает наименьшее значе- ние.

В источнике [8] были получены следующие расчетные оптимальные значения параметров и целевой функции:

w * = - 0,1206; w * = 0,0692; w ₃' = 0,1296; w * = - 0,0065; w * = 0,0294; 1              ,            *2          ,                   3          ,                  4             ,             *5          ,

• a,                                    a,                                               a,       a,                                                                             \       /

  v 1 = 0,5809; v = 0,2610; I ( w , v ) = 0,0244.

Качественный и численный анализ системы (9) показал, что система является вычислительно неустойчивой ввиду существования собственного числа, соответствующего переменной x ₁ , которое имеет достаточно большую положительную вещественную часть. При численных расчетах этой системы обнаружилось расхождение между решением исходной системы (9) и идентифицируемой системы (10) с расчетными значениями параметров (12). Поэтому была поставлена и решена вспомогательная задача идентификации параметров системы (10):

y = U 1 У 1 + u 2 y 2 + u 3 y 3 + u 4 y 4 + u 5 y 5 + U 6 y 6 + u 7 y 7 + u 8 ,

Ут = 0,0123 ( y i - y 2 ) , У з = 0,03 ( y i - y 3 ) , y 4 = 0,112 ( y i - y 4 ) ,     (13)

y 5 = 0,301 ( y i - y 5 ) , У б = 1,149 ( y i - y 6 ) , У 7 = 3,012 ( y i - y 7 ) ,

У 1 (0) = ... = y 7 (0) = 0,25, T = [0,8].

,..., u ₈),

^ф ( ^u ) = £ Е ( y . ⁽ t ) ^- z - ⁽ t ) )² dt ^ min, ^u = ^{( u} i i = 1

где z(t) — приближенное решение, построенное следующим образом. Первые две компоненты вычисляются по модели (10) с расчетными оптимальными значениями параметров (12). Остальные компоненты восстанавливаются по уравнениям исходной модели (9) для переменных y3,..., y7.

Таким образом, z ( t ) является решением системы:

zi =-0,1206z1 + 0,0692z2 + 0,1296, z2 =-0,0065z1 + 0,0294z 2, z3 = 0,03(zi -z3), z, = 0,112(zi -z4), z5 = 0,301(zi -z5), z6 = 1,149(zi -z6), z7 = 3,012(zi -z7), T = [0,8], z1(0) = 0,5809, z2(0) = 0,2610, z3(0) =... = z7(0) = 0,25.

Для численного решения задачи идентификации (13) использовался описанный ранее метод неподвижных точек. Таким образом, были найдены следующие расчетные оптимальные значения управляющих параметров задачи (13):

ui₁ = - 87,9013; u 2 = 8,0383; u₃ = 13,0397; u 4 = 34,0451; u 5 = 22,0533; u₆ = 27,0638; z2 7 =- 14,9313; u₈ = 30,1494; Ф ( ui) = 0,00146.

В результате в качестве «понижаемой системы» рассматривалась тема (13) со значениями коэффициентов (14).

Минимизируемая целевая функция имеет вид: 82             ₂

^{ф (} w ) = JE ( ^x - ⁽ t ) ^- y. ⁽ t ) ) dt , ^w = ( w i ,..., ^w 5 ) .

сис-

0 1=1

Методом неподвижных точек были получены следующие расчетные значения параметров и целевой функции:

W =- 0,1102; w ₂ = 0,0414; w ₃ = 0,1292;

w ₄ = 0,0371; w ₅ =- 0,0904; Ф ( w ) = 0,0009.

На рис. 1 представлены графики траекторий переменных y ₁, y ₂ численного решения понижаемой системы и траекторий переменных x ₁, x ₂ численного решения идентифицируемой системы (15):

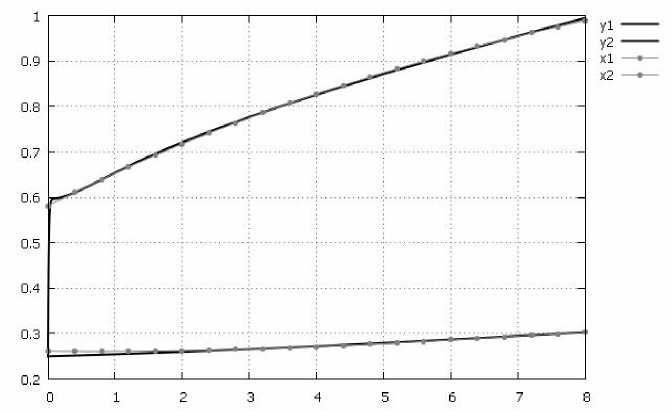
Рис. 1. y ( t ) — решение «понижаемой» системы, x ( t ) — полученное решение

Сравнительный анализ достигнутых расчетных значений целевой функции с известными данными о минимальной среднеквадратичной ошибке, полученными градиентными методами в [1], показал значительно лучшую эффективность метода неподвижных точек.

Предлагаемый метод неподвижных точек продемонстрировал в рамках расчета модельной задачи достаточно широкую область сходимости итерационного алгоритма по начальному приближению, удобство и простоту экспериментальной настройки скалярного проекционного параметра для регулирования качества и скорости сходимости итерационного процесса.

Заключение

Построенный метод неподвижных точек для улучшения управления в рассматриваемом классе нелинейных задач идентификации характеризуется свойством нелокальности, обусловленной фиксированностью параметра проектирования и отсутствием процедуры варьирования улучшающего управления в достаточно малой окрестности улучшаемого управления, характерной для градиентных методов. Предлагаемый метод обладает потенциальной возможностью строгого улучшения неоптимальных экстремальных управлений, удовлетворяющих дифференциальному принципу максимума. Такая возможность появляется в случае неединственности решения задачи о неподвижной точке. Градиентные методы такой возможностью не обладают.

Одно из основных отличий разработанного проекционного метода неподвижных точек от стандартного метода проекции градиента состоит в том, что параметр проектирования a >  0 фиксируется в итерационном процессе последовательных приближений. В методе проекции градиента этот параметр варьируется на каждой итерации приближений для обеспечения улучшения управления.

Указанные свойства предлагаемого метода неподвижных точек являются важными факторами повышения вычислительной и качественной эффективности решения задач идентификации нелинейных динамических систем и определяют перспективное направление развития методов идентификации.