Об одном подходе к поиску экстремальных управлений в дискретно непрерывных системах

Дискретно-непрерывные модели управляемых процессов имеют актуальность, поскольку многие современные приложения (экономические, технические и другие) не могут быть соответствующим образом описаны неизменными в течение рассматриваемого временного интервала дифференциальными уравнениями. В этом случае распространенным методом моделирования является дискретизация по управлению и состоянию, в результате чего появляются модели, неоднородные по своей структуре [1—5].

Такие дискретные модели также могут служить для анализа соответствующих непрерывных задач и поиска их приближенных решений, которые в дальнейшем могут быть использованы как начальные приближения для решений исходных задач. Этот подход прошел апробацию в различных областях [6; 7]. В некоторых объектах управление технически может изменяться лишь дискретным образом [8; 9].

Дискретизация только по управлению была рассмотрена во многих исследованиях (например, [10; 11]). В [12; 13] рассматриваются дискретнонепрерывные модели с кусочно-линейными аппроксимациями управления, в которых состояние системы на интервалах аппроксимации представляется в виде дифференциальных уравнений. В [12] задачи решаются при помощи градиентных методов, которые применяются к эквивалентным конечномерным задачам в пространстве управлений. В [13] для решения эквивалентных конечномерных квадратичных задач используются модификации методов принципа максимума.

В данной статье рассматривается новый подход к решению дискретнонепрерывных задач оптимального управления на основе представления условия оптимальности в форме задачи о неподвижной точке в пространстве управлений. Подход иллюстрируется примерами нахождения экстремальных управлений в задачах на экстремум нормы конечного состояния линейных динамических систем.

1 Метод неподвижных точек

Рассмотрим следующую задачу оптимального управления:

ф( u ) = ф( x (tN ))^ inf (1)

u = { и 1 ,..., U n } eQ

x(t) = fk (x(t), uk, t), x(t0) = x°, uk e Uk ^ Rm(k), t e Tk = [tk-1, tk ],k = 1, N,(2) в которой функция ^(x) непрерывно дифференцируема на Rn, функции fk (x, uk, t), k = 1, N и их частные производные по переменным x, uk непрерывны на множествах Rn х Uk х Tk, к = 1, N. Допустимые управления рассматриваются в виде N -мерных наборов m (k) -мерных векторов u = {u1,..., uN}, uk g Uk, k = 1, N. Обозначим О множество допустимых наборов векторов управлений. Множества Uk с Rm(k), к = 1, N компактны и выпуклы. Начальное состояние x0 и интервалы Тк, к = 1, N фиксированы.

Обозначим через x ( t , v ) , t g T = [ 1 ₀, t_N ] решение системы (2) при управлении v = { v 1 ,..., v_N } gO . Значения x ( t , v ) , t g T_k , к = 1, N определяются путем последовательного интегрирования системы (2) на интервалах Т_к при u_k = v_k , t g T_k , к = 1, N .

Задача (1)-(2) может рассматриваться как задача математического программирования, в которой необходимо найти такой набор векторов u = { U j ,..., u_N } при заданном разбиении интервала времени T на подынтервалы T_k = [ t_k _ 1 , t_k ] , к = 1, N , чтобы выполнялось условие (1).

Введя следующее обозначение частного приращения вектор-функции g ( У 1 , • , У1 ) ^по переменным y s , y_{s 2} ^:

^А Z , Z g ( У 1 , K , У / ) = g ( У 1 , K , ^Z S , , K , ^Z S, , K , У/ ) ^{_ s} 1 s 2                                        x                   ^{1               2}                /

_g(У1, K, yv -,ys2, K, У/), приращение функции (1) на управлениях u, v можно записать:

^Л v ^Ф( u ^{) = Л} x ( t N ,v ) ^ ( x ⁽ t N , u ) ) .                          ⁽³⁾

Также обозначим A x ( t ) = x ( t , v ) - x ( t , u ) , Л u ( t ) = v ( t ) - u ( t ) .

Рассмотрим кусочно-дифференцируемую вектор-функцию

W ( t ) = (^ ( t ) , k , w _n ( t ) ) , t g T с условием:

W ( tN ) = —Px (x (tN ,u)).

Тогда приращение (3) можно записать в виде:

Л v Ф( u ) = - W ( tN ) , Лx ( tN )) + o (||Лx ( tN )||) .

Рассмотрим тождество:

(W (tN ) , Лx (tN )) — ^ (10 ) , Лx (10 )) =

NN

= E (\ w ( ^t k ) , ^{Л x} ( ^t k ))^_ (w ( ^t k _ 1 ) , ^{Л x} ( ^t k _ 1 )) ) = E ^J k . к = 1                                                                     к = 1

Дифференциальная сопряженная система на интервалах Т_к , к = 1, N с переменными у _к ( t ) = ( w ^ ( t ) , ••■, W t ( t ) ) может быть определена при помощи функции Понтрягина Н_к в следующем виде:

^W k ( t ) = - H,_x ( w , ( t ) , ^x ( t , u ) , u k , t ) , t ^e T k с условиями:

Wn ( tN )= V (tN ), Wk (tk ) = Wk+1 (tk ), k = 1, N - 1.

Определим функцию w ( t ) , t g T следующим образом:

W (t ) = Wk (t), t G Tk, k = 1, N.

Каждое из слагаемых Jk, k = 1, N в тождестве (4) может быть записано следующим образом :

J k = (w_k ( t_k) , ^{A x} ( t_k)}- {w_k ( t k - 1 ) , A x ( t_k - 1 )) = j T dt ^_к ( t ) , A x ( t )) dt =

= IT { W k ( t ) , Ax ( t )) + (Wk ( t ) , A x (t, v), vf ( x (t, u ) , uk , t ))} dt =       (5)

= j . - (Hkx (Wk ( t)’ x (t’ u ), uk, t ), Ax (t )V , dt

T k [ ^+A x ( t,v ) ,v_t ^H k ( W k ⁽ t ) , ^{x (} t , u ) , uk , t ) J

В соответствии с [14; 15] (5) может быть представлено в виде: ^J k = I T ^A v k ^H k ( W k ( t ) , ^x ( t , v ) , u k , t ) ^{dt +} o (||^A u k 11) .

Тогда (3) принимает вид:

A . Ф ( u ) -- £ I T A v H k ( w . ( t ) , x ( t , v ) , u , , t ) dt + o ⁽ £ |A u ,\[ k = 1 ^k                                                    У k = 1          J

Введем следующую систему для переменной w ( t ) , t g T :

W (t) = -H,x (w (t), x(t), w,, t), t G T,, k = 1, N с начальным условием:

.

W (tN ) = -Px (x(tN )) .

Пусть w (t, v), t g T = [10, tN ] — решение системы (7)-(8), полученное путем последовательного интегрирования на интервалах Tk, k = 1, N при wk = vk, t g Tk, k = 1, N, x (t) = x (t, v), t g T. Тогда приращение (6) принимает вид:

N r                            (

^A v ^ф( u ) =- XJ T ^A v , ^H k ( w ( t , u ) , x ( t , u ) , u_k , t ) dt ⁺ o I EII^A u k || I . ⁽⁹⁾ k = 1 k                                                      У k = 1 J

Из (9) следует формула, в которой главная часть линейна по приращению управления:

(

^A v ^ф( ^u ) =- EL \^Hk ( w ( t , ^u ) , x ( t , ^u ) , ^u , , t ) , ^A uk}dt ⁺ o I U^A u k || I . ⁽¹⁰⁾

k = 1 k ' u                                               '           У , = 1           J

В линейной по управлению задаче (1)-(2), когда функции f_k , k = 1, N линейны по u , формула (9) совпадает с формулой (10).

На основе формулы (10) получаем необходимое условие оптимальности в задаче (1)-(2) для управления u gQ в следующем виде:

N

^f T \^H k _U ( у ( t ’ u ) ’ x ( t ’ u ) ’ u k , t ) ’ w k k = 1 ^k '

—

u^dt < 0, w = { w _p .K w N } , (11)

W k g U k , k = 1, N .

Представим неравенство (11) в виде эквивалентной системы:

uk^dt <  0, w g U k , k = 1, N .

! _Ti(^Hk_U ^У ( t ^, u ) ^, x ( t ^, u ) ^, u^k , t ) ^, w

—

Данную систему можно представить в виде системы уравнений

U k = argmax f T ^H^ ( у ( t , и) , x ( t , и ) , u_k , t ) , w^dt , k = 1, N .     (12)

Для поиска экстремальных управлений можно использовать известные градиентные методы, основанные на формуле приращения (10).

В данной работе предлагается поиск экстремальных управлений на основе решения задачи о неподвижной точке (12) в пространстве допустимых управлений u = { u 1 , к , u_N } .

2 Примеры

Рассмотрим иллюстрирующие примеры поиска экстремальных управлений, основанные на предлагаемом подходе неподвижных точек.

Пример 1. Рассматривается задача оптимального по энергии управления гармоническим осциллятором [16; 17]. Дискретно-непрерывная аппроксимация задачи рассматривается в классе кусочно-постоянных управлений на интервале T = [0; п] с точкой

0 = -

1 2

разделяющей ин-

тервал T на два непересекающихся интервала 0 = 0 ₀ <0 1 < 0 ₂ = п : X 1 = x ₂; x ₂ =— x 1 + u ; x 1 ( 0 ) = — 1; x ₂ ( 0 ) = 1;

|u ( t )| <  1; t g T = [ 0; - ] ;

^ф( u ) = 2 ( x 1 ² ( ^- ) + x 2 ( ^- ) ) ^ extr.

1.1. Задача на минимум целевой функции:

ф ( u ) = ¹ ( х 2 ( п ) + х ,² ( п )Ц inf .

2^              ^2У          uVV

Функция Понтрягина и стандартная сопряженная система имеют вид:

H ( у , х , u , t ) = ^ у , f ( х , u , t )^ — F ( х , u , t ) = i / 1 x ₂ + у ₂ ( u ■ =_— H ■ У = ^{— H} 1 = у 2 ; ^y k      ^xk ^; у 2 = ^{— H} x ₂ = ^— У 1 ;

— X 1 ) ;    (13)

Wk (ti)= 2 (x(ti)); ti = п; w(x(ti ))=2(x2 (n)+x22 (п));

Wi (п) = -^x (x(ti)) = -xi (n); w2 (n) = -^x2 (x(ti)) = -x2 (п).

Для допустимого u = { u_i; u ₂ } определим:

— при t е T =

0; - :

x_i ( t , u ) = - ( i + u_i ) cos ( t ) + sin ( t ) + u _i;

x ₂ ( t , u ) = ( i + u_i ) sin ( t ) + cos ( t ) ;

— при t e T ₂ =

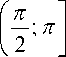
x _i ( t , u ) = - ( u_i + i ) cos ( t ) + ( i + u_i - u ₂ ) sin ( t ) + u ₂; x ₂ ( t , u ) = ( u_i + i ) sin ( t ) + ( i + u _i - u ₂ ) cos ( t ) .

Отсюда получаем систему, одинаковую на интервалах T ₁ и T ₂ :

W _i ( t , u ) = ( u_i + u ₂ + i ) cos ( t ) + ( u ₂ - u_i - i ) sin ( t ) ;

W ₂ ( t , u ) = - ( u_i + u ₂ + i ) sin ( t ) + ( u ₂ - u _i - i ) cos ( t ) ,

t g T = [ 0; п ] .

Используя функцию sign ( z ) , определяемую следующим образом:

sign ( z ) =

- i, z <  0;

j+ i, z >  0;

_ w g [ - i; i ] , z = 0,

и с учетом того, что H_u ( w , x , u , t ) = w ₂ ( t , u ) , задача о неподвижной точке необходимого условия оптимальности (12) принимает следующий вид:

^u i = sign ( J T w 2 ( t , u ) dt ) ;

u ₂ = sign ( J W ₂ ( t , u ) dt ) .

Вычислив интегралы, получаем систему уравнений: u _i = sign ( - 2 ( u _i + i ) ) ; u ₂ = sign ( - 2 u ₂ ) .

Перебрав девять возможных случаев, определяющих значения правых частей системы (i8), находим единственное решение u = { - i;0 } , являющееся оптимальным управлением рассматриваемой задачи. Соответствующее значение функционала составляет Ф ( u ) = 0 .

1.2. Задача на максимум целевой функции:

^ sup.

u e V

ф(u )=2 (x2 (п)+x 2 (п

Преобразуем задачу на максимум в эквивалентную ей задачу на минимум:

ф1 (11) = -2(x2 (п) + x22 (п)) ^ inf •

Функция Понтрягина и стандартная сопряженная система сохраняют вид (13)–(14), а граничные условия (15) для сопряженной системы принимают вид:

^1 (П) = -ф (x (t1 )) = Х1 (П ); V2 (П ) = -Vx2 (x (t1 )) = x2 (П )•

Фазовые траектории на интервалах T ₁ и T ₂ сохраняют вид (16)–(17).

Получаем следующую сопряженную систему, одинаковую на интервалах T ₁ и T ₂ :

V , ( t , и ) = - ( u , + u ₂ + 1 ) cos ( t ) + ( u₁ - u ₂ + 1 ) sin ( t ) ;

t g T = [ 0; п ] .

V ₂ ( t , u ) = ( u₁ + u ₂ + 1 ) sin ( t ) + ( U j - u ₂ + 1 ) cos ( t ) ,

Соответственно получаем систему уравнений:

u1 = sign (2 (u1 +1)); u 2 = sign (2 u 2), имеющую следующее множество решений:

{ u = { 1;1 } ; u = { 1; - 1 } ; u = { 1; 0 } ; u = { - 1; 1 } ; u = { - 1; - 1 } ; u = { - 1; 0 } } •

Из указанного множества максимум Ф ( u ) = 5 исходному функционалу доставляют управления u = { 1;1 } и u = { 1; - 1 } •

Пример 2. Задача на экстремум нормы конечного состояния для двухступенчатой системы [16; 18]. Дискретно-непрерывная аппроксимация задачи рассматривается в классе кусочно-постоянных управлений на интервале T = [0; 2] с точкой 01 = 1, разделяющей интервал T на два непе- ресекающихся интервала 0 = 00 < 01 <02 = 2 :

x ₁ = x ₂; ,x ₂ = u ; x ₁ ( 0 ) = 2; x ₂ ( 0 ) = - 1;

| u ( t )| < 1; t g T = [ 0;2 ] ;

^ф( ^u ) = 2 ( ^x 12 ( ² )^{+ x} 22 ( ² ) ) ^ ex*-

• 2.1.    Задача на минимум целевой функции:

^ф( ^u ) = 2 ( x ( ² )^{+ x} 22 ( ² )H u nf •

Функция Понтрягина и стандартная сопряженная система имеют вид:

H ( v , x , u , t ) = ( v , f ( x , u , t )) - F ( x , u , t ) = V 1 x 2 + V 2 u ;        (19)

. _ „ . V =-Hx = 0;

• ^{V k      x} k ^; | ^V 2 = ^- H l ₂ = ^- V 1 ;

  
  

V k ( t i ) = ^— ^ _k ( x ( t i ) ) ; t i = 2; H x ( t i ) ) = |( x i ² ( ² )⁺ x 2 ² ( ² ) ) ;

Vi (2) = —^xi (x (ti )) = — xi (2 ); V2 (2 ) = ^x2 (x (ti )) = — x2 (2).

Для допустимого u = { u _i; u ₂ } определим:

— при t e T_i = [ 0;i ] :

t '

x ( t , u ) = u--1 + 2;

i                 i 2

x ₂ ( t , u ) = u_i t — i;

— при t е T 2 = ( i; 2 ] :

x ₁ ( t , u )

t ²

= ^u 2 2 + ⁽ u ¹

—

ul. — u. ₊ 2;

x ₂ ( t , u ) = u ₂ 1 + u_i — u ₂ — i.

Отсюда получаем систему, одинаковую на интервалах T ₁ и T ₂ :

Vi (t,u ) = — 2 ui

—

u ; 2²

( \ ( 3 i y 2 (t, u) = I —ui + —u 2

t e T = [ 0; 2 ] .

t — 4 u_i — 2 u ₂ + i,

Поскольку H u ( y , x , u , t ) = v 2 ( t, u ) , задача о неподвижной точке принимает следующий вид:

u1 = Sign u 2 = Sign

Вычислив интегралы, получаем систему уравнений:

u_i = sign I —

u ₂ = sign I —

13 u

7 u

7 J 4^u 2 ⁺ 11;

u _? + 1 .

4 ² J

J 3

Данная система имеет единственное решение u = j ^_ ~ ;i, являющееся оптимальным управлением рассматриваемой задачи. Соответствующее значение функционала составляет Ф ( u ) ~ 0,038 .

• 2.2.    Задача на максимум целевой функции:

^ф( ^u ) = Д ( x i ² ( ² )^{+ x} 22 ( ² ) ) ^ ^SuP.

2^Х                         e V

Преобразуем задачу на максимум в эквивалентную ей задачу на минимум:

^ф 1 ( ^и ) = - 2 ( x ² ( ² ) + x 2 ² ( ² ) ) ^ i nf-

Функция Понтрягина и стандартная сопряженная система сохраняют вид (19)-(20), а граничные условия (21) для сопряженной системы принимают вид:

W1 (2 ) = —^ (x ( t1 )) = x1 (2 ); W2 (2 ) =-^x2 (x (t1 )) = x2 (2 )-

Фазовые траектории на интервалах T₁ и T ₂ сохраняют вид (22)-(23).

Получаем следующую сопряженную систему, одинаковую на интерва- лах T1 и T2 :

W 1 ( t , и ) =

3       1

+ и^ ;

2 1 2 2

3.1 )..,., ,

—и, +— \t + 4 и, + 2 — 1,

2 1 2 2 J 1       2

t е T = [0;2].

Соответственно получаем систему уравнений:

'            ( 13.

и₁ = sign I — и ₁ + —и ₂

.          ( 7.     5.

и ₂ = Sign I — u ₁ + —и ₂

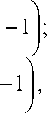
имеющую следующее множество решений:

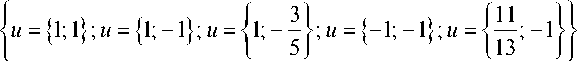
Из указанного множества максимум Ф ( и ) = 6,5 исходному функцио

налу доставляет управление и = { — 1; — 1 } .

Рассмотренные примеры демонстрируют возможность определения оптимальных экстремальных управлений предлагаемым методом непод вижных точек в рассматриваемом классе дискретно-непрерывных задач.

Во всех рассмотренных примерах полученные оптимальные управления совпадают с оптимальными решениями, полученными в работе [16] в рамках альтернативного подхода параметризации управляющей функции.

Заключение

В классе дискретно-непрерывных управляемых систем построено необходимое условие оптимальности в виде задачи о неподвижной точке в пространстве управляющих параметров. Полученная форма условия оптимальности позволяет находить экстремальные управления методом поиска неподвижных точек соответствующей задачи о неподвижной точке. Применение подхода неподвижных точек для решения дискретнонепрерывных задач оптимального управления определяет перспективное направление исследований в области методов оптимального управления.