Об одном принципе оптимальности траекторий в моделях экономической динамики

Рассмотрим модификацию модели Макарова [1], определяемой системой соотношений

K'_M <  v K t + I'_M,  I t„ >  0,

I'_M + at + , L i + <  f ( K t , L t )   ( i = i n)

Предполагается, что в экономике имеется n технологий. Технология i описывается парой ( F , v ) , где F — производственная функция, V — коэффициент сохранности фондов [2, 3]. Модель, которую обозначим Z , задается последовательностью наборов ( F t , v i ; F₂ , v ₂;...; F_n, v _n ) и числовой последовательностью ^{( L}t ) . Под состоянием экономики в момент t в модели Z понимается вектор

( ТУ' 1           n 1         n     1          n

K ,...,K , L ,...,L , a ,..., a )

где K‘ , L i , i = 1, n , объем фондов и численность рабочей силы соответственно, & , i = 1, n - удельное потребление в i- м производстве, причем K i >  0, L i >  0. , В модели (1)

I i означают инвестиции. Считается, что F определена при K > 0, L > 0., дифференци- руемая, неотрицательная, строго вогнутая, положительно однородная, возрастающая по каждой переменной функции, причем F (K ,0) = F (0, L ) = 0 [1-3].

Постановка задачи

Предположим, что в каждой момент времени t каким-то образом общая численность рабочей силы L распределяется по производствам,     т.е.     задан     вектор

L = ( L t ,..., Lt ) , где L i >  0, S n = 1 L = L , .

Таким образом, модель Z определяется вектором (k1,...,Ktn, щ1,...,a"). По набору a = (щ1,...,щп ) построим модель Z(a) и предположим, что ее состояние xt =(K1,...,K", L1,...,Ln) при данном a лежит на эффективной траектории Z(a), обладающей свойством

I , + 1 = K + 1 —V i K , >  0, L , + 1 >  0 (2) и имеющей характеристику ( P ) .

Введем 2 n простейших однопродуктовых моделей Z^l ( p ¹ ),   Z^l ( L‘ ), l = 1, n , задава-

емые одним

i

\

i b^f, b+1 va

bi i     bi i t

t

и

A

тем же набором

Введем следующие обозначения:

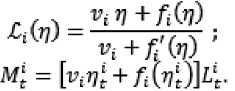
, в которых коэффициен-

ты b‘ , l = 1, n определяются по

характери-

Заметим, что функция является возрастающей. Формула (4) в соответствии с принятыми обозначениями примет вид

стическим ценам ( р ) <  Z ( a ) . В модели Z^l ( L )

состояния

считается

x модели

известным

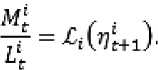
L_t , а в модели Z¹ ( a ¹ ) — удельное потребление a , i = 1, n .

Таким образом, распределив общую численность рабочей силы по производствам, считая L_t+ j >  0 для всех i в силу свойства (2)

Принцип оптимальности

Теперь рассмотрим принцип оптимальности, применяя который можно, с одной стороны, определить состояние модели Z ( L ) , а с другой – состояние эффективной траектории модели Z ( a ) .

Этот принцип оптимальности заключается в следующем: удельное потребление a = a ( L ) выбирается так, чтобы траектория ( K_t, L_t ) с заданной рабочей силой L_t была бы эффективной в простейшей модели ( F , v , a ) , которая получается при данном a .

Докажем последнее утверждение. Последовательность ( K‘_t, L_t ) с фиксированной рабочей силой L t при выборе a как функции от Lⁱ является эффективной траекторией модели Z¹ ( a ^l ) .

Согласно теореме 2.3 [2] такой выбор обеспечивает и эффективность траектории ( x_t ) модели Z ( a ) . Таким образом, последовательность коэффициентов bⁱ позволяет произвести построение моделей Z¹ ( L ) и

траектории, мы однозначно по формулам (3), (4) устанавливаем ставку заработной платы a и определяем состояние xt =(Kt,...,Kn, Lt,...,Ln, at,...,an)

модели Z .

Таким образом, вопрос сводится к распределению рабочей силы. Ниже мы остановимся на одном способе распределения.

Одинаковое удельное потребление

Изучим поведение траекторией модели Z , для которых общая численность рабочей силы считается постоянной и равна единице и ставка заработной платы в каждом из произ-

водств одинакова, т.е. a = a

...

n

= a = a.

Удельное потребление вычисляется по формулам (3), (4). Итак, требуется найти такое распределение общей численности рабочей

силы     L_t+ j, t = 1,... на

^{L l} + 1 ( x n = 1 ^Lt + 1 = 1 ) , ^что

( L t + 1 ) = Р ^( L 2 + ₁ ) =

рабочую  силу

...

= <  ( L + . ) .

Z‘ ( a ^l ), i = 1, n , , связь между ществляет описанный выше мальности.

По теореме 5.1 [2]

которыми осу-принцип опти-

Для решения этой задачи удобно использовать обратную к a‘_t+ j( L^ функцию L_t+ j ( a ^ j) . Из уравнений (3), (4) выразим L_t+l как функцию L_{t + 1} fa _{+ 1} (a t _{+ 1} )) = L_{t + 1} (p t _{+ 1} ) пере-

менной al₊₁

e 0,       .

fhQ -n fvQ ^a t + 1 n t + 1 =            777 i I ,

v+ ft (n+1)

где F +i — единственный корень уравнения fei f fe ik _; ^n t» + ^{f (} n t + i )

L t + 1            V + f F t + , ) '

I V)

Заметим сразу же, что П+1 (a) — возрастающая, а Lt+j (a) - убывающая функции, причем [2]

lim L _{t + 1} ( a ) = +^ , lim L_t+/a ) = 0.

a ^0                      s, a ^—

V

Пусть, далее

s s = min. —

V и   Lt+i(^) + Lt+i(^) + •••+ Lt+i(®) = Lt+i (a)-

Тогда L_t+((a) ) на ( 0, s ) является убывающей функцией и поэтому справедлива

Теорема 1. Уравнение L_t+^® ) = 1 имеет решение тогда и только тогда, когда lim_ffl^ LL_t+ 1( ® ) < 1, , причем указанное решение единственно.

Доказательство. Для функции Кобба-Дугласа [2, 3] s = +® и поэтому s = s .

Откуда lim®^s Lt+i(a) = lim® ... Lt+1(a) = °.

Теорема 1 утверждает, что при определенных условиях существует разбиение общей численности рабочей силы, при котором ставка заработной платы во всех производствах одинаково. Покажем, что такое разбиение единственно. На самом деле, пусть щ₊₁ -одинаковая, для всех ставка заработной платы

( а ,= a ,( L+ ,), y n ,L i ₊1= i).

у t + 1        t + 1 \ t + 1 /" i=H = 1 t + 1       f

Тогда в силу свойств функций п(®) и L(п), определяемых по формулам (3), (4), такому a+i соответствует единственная в каждом из производств численность рабочей силы Lt+[, i = 1, n.

Пусть xt =(KJ,...,K", a',...,®1) - траектория модели Z (L) и во всех соотношениях (1), характеризующих траекторию, реализует- ся равенство.

Положим f ( п ) = F ( п , 1 )-

Рассмотрим одно-продуктовую модель

Z‘ ( L ) =

ii bt^ F, bt^ V, wi bi i,  bi i, t и назовем число bi

Y = -a a t  it ut+1

= max

K , L > 0

v K + F ( K , L ) k + ® l

= max п > 0

^v i V ⁺ ft ⁽ п ) п ⁺ ® t

потенциальными возможностями модели

Z1 (l).

Фондовооруженность

iKi п = ^7 , на ко-

торой достигается максимум в (6), называется оптимальной. Поскольку F и v не меняются со временем, то Y зависит от ® , причем увеличивая (уменьшая) ® мы тем самым уменьшаем (увеличиваем) Yt, т.е. Yi (®) — убывающая функция. Заметим, что потенциальные возможности модели Z1 (L ) совпадают с темпом роста модели (F, v ,®‘t).

Обозначим через а ¹ удельное потребление, выбираемое согласно "золотому правилу Фелпса" по набору ( F , v ) и темпу роста рабочей силы, равному единице. Тогда неймановский темп роста модели ( F_i , v , ® ) равен единице [2, 4], т.е.

"-^fYf = 1 ,        (7)

п1 + а1

где п i — оптимальная фондовооруженность, соответствующая ю¹ . Так как Y_t ( ® ) убывающая функция, то Y_t >  1 при &‘_t <  Ю и Y_t <  1 при а >  ®¹ .

Вернемся к исходной траектории ( x_t ) . Поскольку в соотношениях

K t + 1 i V K + I t + 1 . I t + 1 2 0,

I + 1 + a t + 1 L + 1 i F ( K , L t I  ( 1 = 1л)

реализуется равенство, то получим соотношение, связывающее объемы фондов в соседние моменты времени:

Kt+1 = vKt+ F (Kt, Lt)-®t+1 Lt+1, поделив которое на L , получим

lt где К = ~f .

Справедлива

Лемма 1. Пусть для последовательно сти П выполняются равенства (8) и Г. > 1.

Если ц\ < П, где П i — оптимальная фондо вооруженность, то П.+j < П .

Доказательство. Из (7) и (8) следует равенство

П - П.+1 + ^ - ^+1 = v^+ fl(ni)-

• -1 Vni + fl (п.)]                  ’

l _t

По формуле Лагранжа

f(n)- f,(nt)=ft (o'.П -n\\.

где 0 - точка, лежащая между ц¹ и П , поэтому, учитывая, что 1 , >  1 , получим

П- Y+1 + o - o+i >

• >[v + fM W- nt)

Пусть П < ц‘. Предположим, что ц.+1 > П • Отсюда вытекает, (учитывая, что oi (п)   возрастающая функция), что wi+1 (n+1 )> wi+1 (п)= ^

Это, однако, противоречит (9). Поэтому ^П + 1 <  ^П .

Следствие

Если П <  П и П +1 >  П , то Г . <  1 .

Аналогично лемме 1 доказывается и

Лемма 2. Пусть для последовательности П выполняются (8) и Г . <  1 . Если П . > П , то П + 1 >  n .

Следствие

Если П > П и П.+1 < П , то l‘t > 1.

Пусть П удовлетворяет уравнению o i П ) = o i . В дальнейшем будем считать, что модели Z i ( L i ) занумерованы так, что ^ <  а ²<  ... <  o ⁿ .

Предел последовательности Li  (если существует) обозначим через L, i = 1, n. Предположим, что в каждый момент времени t выполняется условие теоремы 1, т.е. всегда существует Lt такие, что ^ = а и

У L_t i = L_t , i = 1, n , и целью экономической системы является распределение рабочей силы так, чтобы удельное потребление в каждом из производств было одинаковым.

Лемма 3. Пусть при некотором i выполняется неравенство o i <  Щ при всех , . Тогда существует предел последовательности Щ и равен o i .

Доказательство. Пусть   lim p <  o i .

Тогда существует подпоследовательность Щ и 5 >  0 такое, что О <  a ¹ - 3 при достаточно больших k . Далее, поскольку Y ( о ) — непрерывная убывающая функция и Y ( o i ) = 1 , то для любого £ >  0 существует такое 5£ ) , что Y ( o ) > 1 + £ для всех o таких, что o <  o i - 5 ( £ ) . Так как 5 ( £ ) возрастающая функция и 3 ( £ ) ^ 0 при £ ^ 0 , то существует такое £ , что 5 ( i ) <  5 .

Так как Р < o - 5 , то _k

• o. < oi - 5 < oi - 5(£) и

• Yk = Y ° )>1 + £.

Представим национальное богатство в виде м. = м.-1Y = м. - 2Y.-1Y =

...

= M 00 П Y . .

T = 1

где M‘_Q >  0.

Из сказанного легко следует, что

Mi = м0ПY ^+».

Однако в силу того, что о ( ц ) возрастающая функция, из соотношения O_t <  o i следует и соотношение ц‘ <  П .

Поэтому имеем

• м;= vK + F. (K., L, )<

• < vnl + Ft (ni, 1) << +”.

Это противоречие говорит о том, что lim a , >  o i и тем самым lim О . = o i .

Теорема 2

• а )    если а е [ а' , ш ^п ] то и а е О’,а ^п ] для всех , и а ^ О^п , Lⁿ _t ^ 1, L_t ^ 0, i <  n ;

• b )    если ш < ш ¹, то существует момент

времени T : Ш <  ш_т <  ш " , причем ш

( 0, ш J возрастает;

• c )    если ш >  Ш^п и ш >  Ш^п для всех то ш убывает, стремясь к ш ^п .

Доказательство. Докажем, что ш е [ ш , ш ^п ] следует, что ш е [ щ ‘, ш ^п ] .

на

t ,

из

Пусть ц е [ ш ⁱ, ш^п ] Предположим ш₊ 1> ш^п . Тогда ш₊ !> ш , и поскольку ш П ) возрастающая функция, то П _{+ 1} >  П , i = 1, " . Кроме того, П + 1 >  П " >  П . В этом случае 1 " <  1 согласно следствию к лемме 3. Далее, из (4) и (6) следует

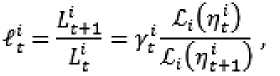
i = 1, n.

Отсюда, учитывая, что – возрастающая функция и Y 1 <  1 , имеем 1 1 <  1. Поэтому l i <  1, i = 1, n , что противоречит условию L 1 + ... + Lⁿ _t = 1 для всех t . Пусть теперь Ш ₊1< Ш ¹. Тогда П ₊₁<  П ¹<  П Привлекая следствие к лемме 2, получим, что 1 1 >  1.

Кроме того, Y t > ¹ и

.

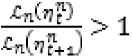
Поэтому из (10) следует, что и l" >  1 . Вновь нарушается условие L = 1 для всех t .

Применяя лемму 3, получим, что ш ^ ш^п . Отсюда вытекает, что для любого s >  0 существует T такое, что для всех t >  T имеет место ш^п — ш <  s .

Пусть     s = а"ш е [ш"-1,ш"], V t > T.

-

п — 1

ю ,

откуда

Следовательно, Y 1 <  1 для всех t >  T и для всех i = 1, n — 1 .

Поэтому национальное богатство Mlt = П _0 Yi ’ М\ в каждом из производств, не считая t , начинает убывать. А в n -м же производстве Y1 > 1 для всех t и потому М" возрастает. Кроме того, последовательность M n ограничена сверху (см. лемму 3).

Следовательно, M i имеет предел Mi , причем M" ^ 0. Далее, поскольку ш ^ шп, п то nt ^ П , где —m = ш • ш (П }

Здесь П >  П , i <  "  и Ц^п = П " .

Поэтому переходя в равенстве (5) к пределу, получим

_;        ^t-I М* .

Um = Um —=      = U ,

^“ f ^^(?7t) ДО?')

причем, Lⁿ >  0 .

Предположим, что и L >  0 , т.е.

М‘ > 0. Тогда, переходя к пределу в (8) и учитывая, что l‘i ^ 1, получим п + ш (ni )=vni+fi (ni}

Из этого равенства вытекает, что П = П . Это невозможно для i <  " , так как п >  п .

Отсюда вытекает, что L = 0, i <  "  и L " = 1.

Доказательство утверждений b ) и c ) аналогично доказательству утверждений b ) и c ) теоремы 1.

Следствие 1. Если ш существует для всех t , то L_t ^ 0, i <  " .

Следствие 2. Суммарное потребление в модели Z в случае, когда общая численность рабочей силы распределяется так, что 0 1 = ш ² = ... = ш = ш стремится к ш^п .