Об орбитах одной неразрешимой 5-мерной алгебры ли

DOI:

Данная статья посвящена изучению задачи о голоморфно-однородных вещественных гиперповерхностях пространства C ³ . Основной интерес в этой задаче в настоящее время связан (см.: [3; 4; 11; 13]) с невырожденными по Леви поверхностями, алгебры голоморфных векторных полей на которых имеют размерность 5.

При этом голоморфным реализациям 5-мерных алгебр в виде алгебр векторных полей на однородных гиперповерхностях часто соответствуют (см.: [1; 2]) вырожденные по Леви орбиты или однородные поверхности с размерностями алгебр симметрии, большими чем 5. В такой ситуации естественно интересоваться просто однородными (Коссовский) поверхностями, алгебры векторных полей на которых являются в точности 5-мерными.

Ниже рассматривается одна из пяти неразрешимых 5-мерных алгебр, обозначенная в [5] через д ₅ и имеющая следующие коммутационные соотношения:

[6 i , 6 2 ] = 2e i ,    [6 i , 6 3 ] = - 6 2 ,    [6 2 , 6 3 ] = 2е з ,    [d, 6 4 ] = 6 5 ,

[6 2 ,6 4 ] = ^е 4 ,   ^[е 2 ^,е 5 ^] = ^{— е} 5 ,   ^[е 3 ^,е 5 ^] = ^е 4 .

Главным результатом статьи является следующее утверждение о локальном устройстве однородных гиперповерхностей пространства C3, являющихся орбитами алгебры (1). Теорема 1. Пусть М — вещественно-аналитическая гиперповерхность в C3, невырожденная по Леви в некоторой точке. Если на М имеется 5-мерная алгебра голоморфных векторных полей со структурой д5, обладающая вблизи этой точки полным рангом, то М голоморфно эквивалентна (индефинитной) просто однородной поверхности

(v - ^y i ) ² + У 2 у 2 = y i ,                              (2)

где z _i , z ₂ , w — координаты в C ³ , х ₂ = Re z ₂ , y _k = Im z _k (k = 1, 2) , v = Im w .

1.    Упрощение базисов алгебр векторных полей

Используя технику работы [8], мы перейдем от рассмотрения абстрактной алгебры Ли (1) к соответствующей алгебре голоморфных векторных полей в C ³ . Элементы базиса такой алгебры будем записывать в виде

6 k = f k (z i ,Z 2 ,w) ^d- + g_k (z i ,Z 2 ,w) ^d- + h_k (z i ,Z 2 ,w) ^d- (k = 1,..., 5).      (3)

UZ i               Oz 2               OW

Здесь f k , g _k , h _k — голоморфные (вблизи обсуждаемой точки поверхности) функции. Для сокращенного представления формулы (3) будем использовать также запись вида

⁶ k ^(f k , ^g k , ^h k ).

Через z _i , z ₂ , w здесь и далее обозначаются координаты в пространстве C ³ . Их вещественные и мнимые части будем обозначать через x _k = Re z _k , y _k = Im z _k (k = 1, 2) , и = Rew , v = Imw . Пару координат (z _i ,z ₂ ) мы часто будем объединять в двумерный комплексный вектор z .

Подчеркнем, что свойство однородности изучается в статье в локальном смысле, то есть речь идет о действиях локальных групп Ли голоморфных преобразований, являющихся транзитивными вблизи некоторой фиксированной точки q поверхности М .

Другими словами, это означает наличие вещественной алгебры Ли g(M ) голоморфных векторных полей, определенных вблизи q и заметающих своими значениями касательные пространства к М во всех точках этой поверхности, близких к q .

Везде ниже будем считать обсуждаемую точку q однородной поверхности М совпадающей с началом координат пространства C ³ .

Из теории дифференциальных уравнений известно (см., например, [6]), что любое гладкое векторное поле можно выпрямить вблизи неособой точки подходящим координатным диффеоморфизмом. В работе [8], развивающей идеи Э. Картана [9], показано, что подобные упрощения можно производить с несколькими полями одновременно. Упрощение даже одного поля с учетом коммутационных соотношений, выполняющихся для конкретной алгебры, влечет за собой возможность упрощения и других полей.

Под упрощением здесь понимается сокращение числа аргументов у функциональных коэффициентов / _k , g _k , h _k полей вида (3). За счет голоморфных преобразований координат часто удается сократить количество аргументов у / _k , g _k , h _k до одного или двух (в случае, когда функциональный коэффициент зависит только от одной переменной Z 2 , мы используем обозначение / _k , g _k , h _k ).

Отметим, что в статье рассматриваются только невырожденные по Леви поверхности. Определяющие функции таких поверхностей зависят от всех трех комплексных переменных, и матрица Гессе (см. [7]) вторых производных, суженная на комплексную касательную плоскость к такой поверхности, является невырожденной эрмитовой матрицей.

Сформулируем здесь три леммы о векторных полях на невырожденных гиперповерхностях, являющиеся уточнениями использованных (и обоснованных) в [8] утверждений.

Лемма 1. Если на невырожденной по Леви гиперповерхности М с C ³ имеется пара коммутирующих голоморфных векторных полей 6 1 и 6 2 , линейно независимых над R , то голоморфной заменой координат эта пара может быть выпрямлена, то есть приведена (вблизи некоторой точки поверхности) к виду

6 1 = (0,0,1), 6 2 = (1,0, 0).

Лемма 2. Пусть два голоморфных векторных поля из базиса 5-мерной алгебры Ли имеют выпрямленный вид 6 1 = (1,0,0) , 6 2 = (0,0,1) , а еще два поля 6 3 , 6 4 имеют специальный вид

6 k = (X(z i ,w) + / k (2 2 ),g k ( z ₂) , L k (z i ,w) + h k (Z 2 )} (k = 3,4) (4)

с некоторыми голоморфными функциями / _k ( z ₂) , g _k ( z ₂) , h _k ( z ₂) и некоторыми линейными функциями l _k (z 1 ,w), L _k (z 1 ,w). Если при этом g ₃ (0) = 0 , то существует голоморфная замена переменных z 1 , z ₂ , w, переводящая поле 6 3 в состояние (l ₃ (z 1 , w), 1, L ₃ (z 1 , w)) и сохраняющая выпрямленный вид полей 6 1 , 6 2 , а также вид (4) поля 6 4 .

Замечание. Уточним, что при замене из леммы 2 голоморфные функции / ₄( z ₂) , g ₄ (z ₂ ) , h ₄ (z ₂ ) из представления поля 6 4 , вообще говоря, изменяются, в отличие от остающихся неизменными линейных функций l ₄ (z 1 ,w) , L 4 (z 1 ,w) .

Лемма 3. Если четверка базисных голоморфных полей 5-мерной алгебры д(М) полного ранга имеет вблизи некоторой точки М вид

6 1 = (/ 1 (Z 1 ,Z 2 ,Z 3 ), 0,h i (z i ,Z 2 ,Z 3 )) ,

6 2 = (/ 2 (Z 1 , Z 2 , Z 3 ), 0, ^(Z x , Z 2 , Z 3 )) ,

6 3 = (/ 3 (Z 1 ,Z 2 ,Z 3 ), 0,^ 3 (Z 1 ,Z 2 ,Z 3 )) ,

64 = (/4^1, Z2, Z3), 0, ^4(Z1, Z2, Z3 )) , то поверхность М является вырожденной по Леви (вблизи обсуждаемой точки).

Отметим, что утверждение леммы 3 вытекает из независимости определяющей функции обсуждаемой поверхности от переменных Z 1 , w при выполнении условий вещественной линейной независимости рассматриваемой четверки полей.

Основная техническая идея доказательства сформулированной теоремы 1 состоит в постепенном упрощении (за счет голоморфных преобразований) нескольких базисных полей. Конкретные шаги таких упрощений аналогичны вспомогательным утверждениям из работы [8]. После нескольких таких шагов алгебры с упрощенными базисами удается проинтегрировать и получить явные уравнения обсуждаемых однородных поверхностей.

2.    Голоморфные реализации алгебры д5

Так как в алгебре д ₅ , задаваемой коммутационными соотношениями (1), два поля 6 1 и 6 5 коммутируют, то, согласно лемме 1, мы можем их выпрямить (в окрестности некоторой точки, близкой к началу координат) до состояния

6 1 =     , 6 5 = или 6 1 = (1,0,0), 6 5 = (0,0,1).

UZ 1        dW

Рассматривая далее коммутационные соотношения [6 1 ,6 4 ] = 6 5 , [6 4 ,6 5 ] = 0 , мы получаем формулы для поля

6 4 = (/ 4 2 ),g 4 (Z 2 ), Z 1 + & _{4 2} )).

Аналогичные рассмотрения коммутаторов [6 1 ,6 2 ] = 26 1 , [6 ₂ ,6 ₅ ] = - 6 5 приводят к формулам

6 2 = (2Z 1 + / 2 (Z 2 ), g 2 (Z 2 ), w + ^ 2^2 )).

В силу леммы 3 можно утверждать, что вблизи начала координат пространства C ³ найдется точка на поверхности М , в которой либо g ₂ (Z ₂ ) , либо g ₄ (Z ₂ ) принимает ненулевое значение. Перенесем начало координат в такую точку и рассмотрим далее два случая упрощения базисных полей:

1-й случай: ^ 4 (0) = 0 ,

2-й случай: 5- 4 (0) = 0 , д 2 (0) = 0 .

Предложение 1. Базис (любой) голоморфной реализации алгебры д ₅ в первом случае можно привести голоморфным преобразованием к виду

6 1 = (1, 0,0),

6 2 = (2Z 1 , - Z 2 , w) ,

6 3 = ( - Z 2 , Z 1 Z 2 - W, - Z 1 W) ,

6 4 = (0,1,Z 1 ), 6 5 = (0,0,1).

Доказательство. Для доказательства предложения 1 рассмотрим базис с учетом уже полученных упрощений отдельных его элементов

6 1 = (1,0, 0),

6 2 = (211 + / 2 (1 2 ), 9 2 (1 2 ), W + h 2 (1 2

6 4 = (/ 4 (2 2 ),9 4 (1 2 ), 1 1 + ^ 4 (1 2 )) ,

6 5 = (0,0, 1) .

Применяя лемму 2 к полям e ₂ , 6 4 , имеющим вид (4), упростим поле 6 4 до вида е ₄ = (0,1,1 1 ) и продолжим рассмотрение коммутаторов, связанных с полем 6 3 .

Из [e ₃ ,e ₅ ] = e ₄ получаем

-

(1 ,1 ,D=(0

, 1,1 1 ),

так что

6 3 = (/ 3 (1), — w + д з (1), -1 1 W + Тц (1)).

Аналогично из [6 1 , 6 ₃ ] = — 6 ₂ получаем

(Hl’ 19 3 ’ ^{— W +} ih ) = ^{— (21} 1 ^{+ /} 2 , ^д 2 ,^{W + h})

и

6 3 = ( — 1 2 — 1 1 / 2 + / з , — W — 1 1 9 2 + 9 3 , — 1 1 W + 1 1 ^ 2 + h l ).

После таких рассмотрений остаются неиспользованными три коммутационных соотношения из десяти, имеющихся в алгебре, а именно

^[e 2 ^,e 4 ^] = ^e 4 , ^[e 3 ^,e 4 ^] = ⁰, ^[e 2 ^,e 3 ^] = ^2e 3 .                             ⁽⁷⁾

Первое из них имеет в развернутой форме вид

(21 1 + Л)(0,0,1) — ( (/ 2 ,9 2 , h 2 ) +1 1 (0,0,1) ) = (0,1,1 1 ),

• и из него можно получить уточнение вида компонент поля

6 2 = (21 1 + ^ 2 , — 1 2 + B ₂ , W + A 2 1 2 + C 2 ).

Здесь A ^ , B fc , C fe — некоторые комплексные константы.

Как следствие, уточняется и вид поля

• ⁶ 3 = (^{— 1 2 — A} 2 ¹ 1 + / з , ^{— W — 1} 1 ^{( — 1} 2 + ^B 2 ) + ^д 3 , ^{— 1} 1 ^W + ¹ 1 ^(A 2 ¹ 2 + О г ) + Н 3) .     (8)

Покомпонентное рассмотрение второго из тройки соотношений (7), то есть

(^{— 1 2 — A} 2 ¹ 1 + / 3 ) ^{(0, 0}, 1) ^— ( ^(/ 3 , ¹ 1 + ^д 3 , ^A 2 ¹ 1 + ^h 3 ) ^{+ 1} 1 ^{(0, —} 1, ^{— 1} 1 ⁾ ) = ⁰ приводит к следующим выводам:

/3 = A3; 93 = B3; A2 = 0, h 3 = A312 + С3, и к уточнению формулы (8) для поля 63. На этом этапе получаем

6 3 = (—z 1 + A 3 , z 1 z ₂ — B ₂ z i — w + B 3 , -z 1 w + С 2 z 1 + A 3 z 2 + С 3 ),

6 2 = (2z i , —Z2 + B ₂ , w + С 2 ).

Наконец, последнее соотношение [е ₂ , 6 3 ] = 2е ₃ примет (с учетом полученных уточнений формул для полей е ₂ , 6 3 ) вид

^2z 1 ^{( — 2z} 1 , ^z 2 ^{— B} 2 , ^—w + ^С 2 ) + ^(—z 2 + ^B 2 ^{)(0, z} 1 , ^A 3 ) + ^(w + ^С 2 ^{)(0, —} 1, ^{— Z} 1 ^{) — — ( — z} 2 + ^A 3 ^{)(2, 0}, ^{0) — (z} 1 ^z 2 ^{— B} 2 ^z 1 ^{— w} + ^B 3 ^{)(0, —} 1, ^{0) — — ( — z} 1 ^w + ^C 2 ^Z 1 + ^A 3 ^z 2 + ^С 3 ^{)(0, 0}, 1) = ^2е 3 .

Расписывая покомпонентно это равенство, получим

A 3 = 0; B 3 + С 2 = 0; — 2C 2 Z 1 — 4A 3 z 2 + (A 3 B 2 — ЗС 3 ) = 0.

Это означает, что

С2 = A3 = B3 = С3 = 0, а вся пятерка базисных полей обсуждаемой реализации алгебры д5 принимает (в первом случае) вид

6 1 = (1,0, 0),

• ⁶ 2 = ^(2z 1 , ^{— z} 2 + ^B 2 , ^w) ,

• ^е 3 = ^{( — z} 2 , ^z 1 ^(z 2 ^{— B} 2 ) ^{— w}, ^{— z} 1 ^w) ,                            ⁽⁹⁾

6 4 = (0, 1,z 1 ) ,

6 5 = (0,0, 1) .

Сдвиг переменной z * = z 2 — B ₂ упрощает этот набор формул до состояния (6). Предложение 1 доказано.

Предложение 2. Голоморфные реализации алгебры д ₅ во втором случае могут иметь только вырожденные по Леви орбиты.

Доказательство. Во втором случае начальные упрощения базиса позволяют записать четверку его элементов в виде

6 1 = (1,0, 0),

6 2 = (2z 1 ,1, w),

6 4 = ^A(z 2 ), 0, z 1 + К 4 (z 2 )) ,

6 5 = (0,0,1).

Обсудим в этом случае еще неиспользованные коммутационные соотношения. Так, равенство [6 ₂ ,6 ₄ ] = 6 4 имеет в развернутой форме вид

2z 1 (0, 0,1) + (/" 4 , 0, К 4 ) — / 4 (2, 0, 0) + (z 1 + К 4 (0, 0,1) = (f 4 (z 2 ) 0, z 1 + K 4 (z 2 )).

Из него следует, что

/ 4 (z 2 ) = A 4 6 ^3z 2 , K 4 (z 2 ) = С 4 6 2 ^{2 2}

с некоторыми комплексными константами A 4 , С 4 , так что

• е 4 ( A. , А ³ ' 2 ,0,2 1 + С 4 е ^2г 2 ).                                      (10)

Рассматривая далее коммутаторы [e 1 ,e ₃ ] = — e ₂ , [e ₃ ,e ₅ ] = e ₄ , получаем следующую информацию о компонентах поля e ₃ :

( 9f 3 дд з 9К з ) 52 1 ’52 1 'dd = ^{— (22 1} ' ¹'^ю),

(>22)='А,-.о.„ г,--^

Это означает, что поле e3 обязано иметь следующий упрощенный вид e3 = (— 22 — ЮА4 e3z2 + /з, -21 + 93(22), -21Ю + ЮС4е2г- + К 3(22)) .

Покажем, что в такой ситуации орбита голоморфной реализации обсуждаемой алгебры может быть только вырожденной по Леви. Для этого рассмотрим коммутатор ^[е 2 , ^е 3 ^] = ^2е 3 -

В развернутой форме получаем здесь

22 1 ( — 22 1 , — 1, — w) + ( 3A 4 we ³ ' ^- + / 3 , 9 3 , 2C 4 we^{2 z} 2 + К 3 ) +

+ w(—A 4 e ^3z 2 ,0, — 2 1 + C 4 e ^2z 2 ) — ( — 2 2 — wA 4 e ^3z 2 + / 3 )(2, 0, 0) —

• — (—2₄w + WC4 e^{2 z} 2 + К 3 )(0,0,1) = 2e 3 .

Первая компонента этого векторного равенства имеет вид

— 42 2 + ( З.Ап ³ ' ^- + / 3 ) — A 4 we ^3z 2 — 2( — 2 2 — wA. , A^{3 -} + / 3 ) = 2( — 2 2 — wA „ A ³ ' ^- + / 3 ) или

2A 4 we ^3z 2 + (/ 3 — 4/ 3 ) = 0.

Последнее равенство формально содержит переменные 2 2 и w (слагаемые с переменной 2 1 автоматически сократились). Необходимым условием его тождественного выполнения является равенство A 4 = 0 . Но в силу (10)

e ₄ = (0, 0, 2 1 + C 4 e ^{2z -} ).

Наличие в обсуждаемом базисе еще и поля e ₅ = (0, 0,1) означает, что определяющая функция Ф(2 1 ,2 2 , w) любой интегральной поверхности алгебры с таким базисом не зависит от переменной w . Следовательно, все такие поверхности (если они существуют) вырождены по Леви.

Предложение 2 доказано.

Замечание. Вопрос о существовании или невозможности существования таких вырожденных однородных поверхностей мы здесь не обсуждаем.

3.    Получение уравнения однородной гиперповерхности

Теперь мы получим уравнения однородных поверхностей, являющихся орбитами алгебры (6). Уравнение каждой такой поверхности М ищем в виде и = F (У1,Х2,У2).

При этом определяющая функция Ф = — v + F поверхности удовлетворяет системе трех уравнений в частных производных

Re ( е _к (Ф) | _м ) = 0, (к = 2,3,4).

Аналогичные уравнения, отвечающие полям е 1 , е ₅ и означающие независимость определяющей функции Ф от переменных Х 1 , и , фактически уже учтены в виде (11).

Итак, тройка уравнений (12) имеет в вещественной форме вид

9_?. ЭР „ ЭР

^2у 1 дУ 1 - ^Х 2 9^ 2

-

У 2 дР — ^F = ^0,

- 2Х 1 У 1 д^р- + (Х 1 Х 2 — У 1 У 2 — и) d^l + (Х 1 У 2 — Х 2 У 1 — F ) д^Р- + (x i F + у г и) = 0,    (13)

дР ,  дж ;

^— У 1 = 0.

Заметим, что во втором уравнении системы (13) имеются две группы слагаемых, содержащих переменные Х 1 и и . Но с учетом первого и третьего уравнений каждая такая группа тождественно равна нулю. Поэтому получаем упрощенный вариант системы (13) в виде

2У1 дР

У ¹ ду -

-

„ ат

^Х 2 дж ;

-

У 2 g— ^F = ^0,

^{— у} 1 ^у 2 дЖ ; + ^(х 2 ^у 1 - ^F ) Ц; = ⁰,

дР ,  дж ;

^— У 1 = 0.

Решение самого простого из этих уравнений F(у1,х2,у2) = Х2у1 + G(у1,у2) с произвольной аналитической функцией G(у1,у2) подставим в два оставшихся уравнения системы (14). Эти два уравнения имеют теперь вид dG

2у_ч-ОУ 1

-

dF _ dG _ у2dy = G,  Gdy =

-

У 1 У 2 .

Решение первого из них есть функция вида

1 С⁽У 1 ^,У 2 ⁾ = — Ф⁽У 1 У 2 ) У 2

с произвольной функцией одного переменного ϕ .

Тогда последнее уравнение изучаемой системы примет вид ОДУ

^^‘Ш - н = -^2, где ^ = У1У2, н = Ф2.

Решение этого ОДУ н = — ^ ² + С ^ с произвольной вещественной константой С позволяет записать решение системы (13) в виде

(Gу 2 ) ² + (у 1 У 2 ) ² = С (У 1 У 2 ).

После сокращения уравнения (15) на у 2 = 0 и перехода к исходным переменным задачи получаем уравнения искомых однородных поверхностей в виде

( v — / 2 У 1 ) 2 + У 2 у 2 = Cy 1 .

Остается заметить, что при C = 0 уравнение (16) описывает не 5-мерную (гипер) поверхность, а объединение двух вещественных 4-мерных поверхностей

Г = { У 1 = 0, V = 0 } и Г = { у 2 = 0, V = Х 2 У 1 } в комплексном пространстве C ³ .

При C = 0 замена

^Z 1 ^ (с) ^Z 1 ’ ^Z 2 ^ ^{C Z} 2

превращает параметр C этого уравнения в единицу, а само это уравнение задает индефинитную вещественную гиперповерхность (2).

Теперь для завершения доказательства теоремы 1 остается убедиться в простой однородности этой поверхности.

4.    Нормальные формы и задача об однородности

Ответы на многие вопросы, связанные с вещественными гиперповерхностями комплексных пространств, удается получать с использованием понятия нормальной формы Мозера (см. [10], а также [3; 4]).

Напомним, что уравнение всякой невырожденной по Леви вещественно-аналитической гиперповерхности М С C3 может быть приведено (вблизи любой своей точки) к виду v = {z,z} + N220 (z,z) + .... (17)

Здесь ( z, z ) — невырожденная эрмитова форма (форма Леви поверхности), N ₂₂₀ ( z,z ) — однородный многочлен бистепени (2, 2) по переменным z = (z 1 ,z ₂ ) и Z = (Z ₁ ’Z ₂ ) , а многоточия означают слагаемые более высоких степеней по переменным z , Z , и = Rew . При этом многочлен N 220 является элементом специального пространства Ы ₂₂ многочленов бистепени (2’ 2) , определяемого формой Леви поверхности.

Процедура приведения к такой нормальной форме является вполне конструктивной, хотя и достаточно громоздкой в силу ее многошагового характера. Для целей нашей статьи достаточно обсудить многочлены N 220 из уравнений вида (17) для нескольких семейств однородных поверхностей.

Относительно подробно мы рассмотрим нормализацию уравнения (16) при C = 1 , то есть

(v -Х2У1У + У2У2 = У1’ переписанного (после замены z = iz*) в виде

V =

^— ^ 1 ^У 2 +

Х 1 — ^ 1 ^ 2 .

Точкой поверхности, вблизи которой проводится нормализация, выберем Q(1, 0, i) G G C 3 . Разложение функции

^F = ^{— 1 — (1} + ^ 1 ^{) у} 2 + у^Т+хи -■ ⁽¹ + X 1 ^{) 2} ^ 2

в степенной ряд имеет вид

v — Fi + F2 + F3 + F4 + ..., в котором отдельные тейлоровские компоненты определяются формулами

1 2    1 2             1   3    3     2                5         3  2 2

F2 — —Ж1У2--Жч--Ж9,   F3 — --ж3--тЖчЖо,   F4 —--Жч--ЖчЖ9ж4.

• 2        1У2    8 1    2 2,     3    16 1    4 1 2,     4       128  1    16 1 2

При возвращении к комплексным переменным (с одновременным растяжением координат по формулам ж _к — z _k + z _k ) получаем

F2 — — 8 (z1 + Z1) + г (z1 + Z1) (z2 — Z2) — 2 (z2 — и эрмитову часть этого многочлена, то есть форму Леви обсуждаемой поверхности,

H(z, z) — ZZ2Z1 — ZZ1Z2 — Z2Z2 — 4Z1Z1.(19)

Для приведения этой формы к виду

H — Z 1 Z 2 + Z 2 Z 1

воспользуемся линейной заменой координат z1 — ^ (z* + z2),

Z 2 —

г f"2=(z*

к Уз ¹

+ ^Z * ) + ^{( z} * ^—

Z * )) ,

w — 2w * .

Замечание. Приведение эрмитовой формы к каноническому виду может быть реализовано различными линейными преобразованиями. Выбранное нами преобразование обеспечивает при переходе к комплексным координатам наличие только вещественных коэффициентов у наиболее важных при нормализации многочленов F ₃ , F 4 .

Вторым шагом после такой замены освобождаем полученное уравнение v — (Z1Z2 + Z2Z1) + F3(z, z) + F4(z, z) + . . .

от слагаемого F ₃ . При этом голоморфные слагаемые, входящие в F ₃( z,z ) (как, впрочем, и в остальные F _k ( z, Z) при к >  1 ), не оказывают влияния на старшие компоненты нормализуемого уравнения и «просто удаляются» из него (см. [10]).

Еще одна группа слагаемых из F ₃( z, Z) имеет вид

Q 1 ( z ) Z 1 + Q 2 ( z ) z 2

с квадратичными формами q1(z) — ^i + 2Тз) z2 + ^2 - Уз^ z1z2 + ^-2Уз +1^ Z2,

^Q 2 ^{( z ) —} ^^— 2 У^{3 —} 1^ ^Z 1 + (^{— 2 —} Уз ) ^Z 1 ^Z 2 + ^2 У^{3 —} 1) ^Z 2

от двух комплексных переменных z 1 , z ₂ .

С учетом (22) мы строим квадратичную вектор-функцию / ₂ (z) = (Q 2 (z), Q _i (z)) и поправочное слагаемое

△ 22 = —( / 2 , / 2 ) = ^— ^ ^Q 2 ^(z)Q i ^{(z) + Q} i ^(z)Q 2 ^(z) ^ .

После замены

z * = z + / 2 + ..., w * = w + . . .

уравнение нормализуемой поверхности примет вид

V = (ziz2 + z2z1) + H22(z, z) +    ^2   Hkl(z,z), k,l>2,k+l>5

где H 22 = F 22 + A 22 .

Приведем развернутую запись многочлена

^H 22 = ^A i ^{| z} i | 4 + A^Z i ^{| 2 | z} 2 | ² + ^A 3 ^{| z} 2 | 4 + (B^z 1 ^z i ^z 2 + 13 ^z i ^z 2 ^z 2 ) + + (CZ i Z 2 ^z 2 + C Z 2 ^Z 1 ^Z 2 ) + (DZ1Z 2 + D Z 2 Z 2 ),

каждый моном которого имеет вторую степень по переменной z и вторую — по z .

В нашем случае все коэффициенты этого многочлена являются вещественными и определяются формулами

A i

-

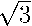
^А 2 =

3,

B = 7 + ^А

3   V 3

C=3

-

^{А з} = ^— 3 ⁺ 7 1’

4=, D = ².

/3’         3

При этом при «простейшей нормализации» многочлен N 220 из нормального уравнения обсуждаемой поверхности (21) равен (см.: [3;4]) проекции многочлена H ₂₂ в пространство Ы ₂₂ .

Лемма 4 ( предложение 1.2, [3] ). В случае формы Леви (z,z ) = z 1 z ₂ + z ₂ Z _i проекция многочлена (23) в пространство Ы ₂₂ описывается формулами

(^F 22⁾. V = A i | ^z i | ⁴ + ^A 2 ( ^{4 | z} i ^{| 2 | z} 2 | ^{2 —} (Z 2 Z 2 + ^z 2 ^{z 2 )} ) + A 3 ^{| z} 2 | 4 +

+ 2^i(z2ziz2 - ziz2z2) + i^2(ziz2Z2 - z^iz2), где

A i = A-у, A 2 = — ( A ₂ — 2 Re D), A 3 = A 3 , Ц4 = Im B, p. 2 = Im C.

В силу этой леммы получаем набор коэффициентов ( A _i , A _i , A _i , p _i , p ₂ ) многочлена N ₂₂₀ из нормального уравнения поверхности (18), равный

(—

—

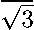
9,

+4=, °, °). V3

Растяжение переменных с одновременной симметрией

Z _i ^ — rtZi, z ₂ ^ -z ₂ , w ^ — r ² w

сохраняет нормальный вид уравнения (17) и форму Леви х1х ₂ + х ₂ х 1 обсуждаемой поверхности при произвольных положительных г , t .

Ненулевые коэффициенты многочлена N 220 изменяются при замене координат (25) по формулам

Ai ^ -^^Xi, А2 ^ -г2Л2, Аз ^ -—Аз и становятся положительными.

Полагая t ⁸ = А 3 / А 1 , г ^-4 = А 1 А 3 , мы превратим набор (24) в

^{( A} 1 , ^X 2 , А з , ^ 1 , ^ 2 ) = f

• 1,    3,1, 0, с) .                                  (26)

Итог описанной нормализации поверхности (18) можно сформулировать следующим образом.

Предложение 3. Существует нормальное по Мозеру уравнение вида (17) поверхности (18) , в котором коэффициенты многочлена N 220 имеют вид (26) .

Отметим, что такой набор является частным случаем наборов типа 1 из предложения 1.5 в [3]. В силу теоремы 3.6 из этой же работы размерность алгебры симметрий обсуждаемой поверхности не превышает 6.

Предложение 4. Поверхность (18) является просто однородной , то есть ее максимальная алгебра симметрий является в точности 5-мерной.

Доказательство этого утверждения следует из сравнения голоморфно инвариантного набора (26) с аналогичными наборами для однородных гиперповерхностей пространства C ³ , имеющих «богатые» алгебры симметрий и индефинитную форму Леви (20).

Согласно результату [11] (теорема 1.1), для любой голоморфно-однородной невырожденной по Леви вещественной гиперповерхности М С C ³ с нетривиальной алгеброй симметрий справедливо хотя бы одно из следующих утверждений:

• 1.    М голоморфно эквивалентна квадрике v = | z 1 1 ² ± | г ₂ | ² (и тогда многочлен N 220 в любом ее нормальном уравнении является нулевым),

• 2.    М голоморфно эквивалентна одной из трубчатых поверхностей приведенного в работе списка (содержащего 21 тип уравнений),

• 3.    М попадает в картановский или винкельманновский тип.

Остается уточнить, что поверхности картановского (и псевдо-картановского, см. [3]) типа имеют номер 4 в упомянутом выше классификационном предложении 1.5 из [3], а винкельманновский тип имеет в этом предложении номер 6.

Из 21 типа трубчатых поверхностей работы [11] 6-мерные алгебры симметрий имеют лишь 12 типов, включенных в таблицы 7 и 8. При этом все поверхности, попавшие в таблицу 7, имеют сводимые к винкельманновскому типу уравнения вида

V = ф ( Х х ) х ₂ + ^ (Ж 1 ).

В частности, это 8 типов поверхностей, имеющих 6-мерные алгебры симметрий ( α и β — вещественные параметры):

V = Х 1 Х 2 + х а , V = Х 1 Х 2 + 1пХ 1 , V = Х 1 Х 2 + Х ^ 1п Х 1 , V = Х 1 Х 2 + Х 3 1пХ 1 ,

V = Х 1 Х 2 + е ^ж 1 , V СО8Х 1 + х ₂ sin Х 1 = е ^вж 1 , V = Х 2 е^ж 1 — Х 21 ,

В таблице 8 имеется 4 типа поверхностей с 6-мерными алгебрами симметрий. Это

VX 1 = X 2 — £ X 1 , V = X 2 + £ X 1 , V = X 2 + £ X 1 ln Х 1 , V + £ 1 X 1 + £ 2 X 2 = 1,     (27)

где a G R , £ , £ 1 , £ 2 = ± 1 .

Отметим, что в этом списке содержатся уравнения поверхностей как с индефинитной, так и с положительно определенной формой Леви. При этом индефинитные поверхности из (27) приводятся несложными преобразованиями, аналогичными описанным в начале этого раздела, к виду

^V = ( | ^ 1 | 2 ^— | ^ 2 | 2 ) ⁺ ( | ^ 1 | 4 ⁺ 4 | ^ 1 ^{| 2 |} ^ 2 | ² + | ^ 2 | 4 ) + . . . .

Такой вид соответствует, согласно [3], так называемым псевдо-картановым поверхностям, входящим в качестве отдельного подтипа в тип 4 классификационного предложения 1.5 из [3].

Тем самым предложение 4, а с ним и основной результат настоящей статьи — теорему 1, можно считать доказанными.

Замечание. Вопрос о возможной голоморфной эквивалентности поверхности (18) какому-либо известному однородному многообразию с 5-мерной алгеброй симметрий мы здесь не рассматриваем. Семейство известных однородных (и, в том числе, просто однородных) поверхностей достаточно велико. Например, оно содержит все трубчатые многообразия над аффинно-однородными поверхностями из R ³ (обширный полный список таких поверхностей получен в [12]). Детальный анализ всего этого семейства в связи с обсуждаемой задачей выходит за рамки настоящей статьи.