Об осциллирующих решениях автономных дифференциальных уравнений с последействием

Как показали самые первые исследования уравнений с последействием [1], их решения, начиная с линейных уравнений первого порядка, могут иметь любое (в том числе и бесконечное) множество нулей. Это обстоятельство сделало актуальной задачу отыскания осциллирующих решений уже для скалярных функционально-дифференциальных уравнений. Решение данной задачи было начато с уравнений с сосредоточенным запаздыванием [1–5], которым до сих пор посвящена большая часть исследований (см. монографии [6–8] и библиографию к ним). Для этих уравнений необходимым и достаточным условием осцилляции всех решений является отсутствие вещественных нулей у характеристического квазиполинома [2, 6, 7]. Для уравнения с одним сосредоточенным запаздыванием X ( t ) + ax ( t - h ) = 0 на основе этого критерия

Работа выполнена в рамках госзадания Министерства образования и науки Российской Федерации (задание №2014/152, проект № 1890).

был найден коэффициентный признак осцилляции: все решения данного уравнения осциллируют тогда и только тогда, когда ah > ¹.

e

С развитием теории функциональнодифференциальных уравнений был найден удобный общий вид линейных автономных уравнений с последействием в форме интеграла Римана–Стилтьеса [9, 10]. Такая запись позволяет рассматривать одновременно и сосредоточенное, и распределенное запаздывание и устанавливать факты, общие для всего класса автономных функционально-дифференциальных уравнений.

В настоящей работе для автономного дифференциального уравнения с ограниченным последействием доказан критерий осцилляции решений в терминах нулей характеристической функции. Полученный результат был применен к уравнениям с двумя запаздываниями различной природы и позволил получить для них эффективные признаки осцилляции.

• 1.    Постановка задачи. Пусть N – множество натуральных; R – вещественных;

• 2.    Основной результат

R + - вещественных неотрицательных; С -комплексных чисел.

Рассмотрим линейное автономное дифференциальное уравнение с ограниченным последействием:

x ( t ) + f 0° x ( t — s ) dr ( s ) = 0, t ^G R ₊ , (1) где ю >  0, функция r : R ₊ ^ R имеет ограниченную вариацию, r ( 0 ) = 0. Интеграл понимается в смысле Римана–Стилтьеса. Следуя [11], назовем решением уравнения (1) локально абсолютно непрерывную функцию, удовлетворяющую (1) почти всюду. При отрицательных значениях аргумента полагаем решение доопределенным заданной начальной функцией.

Определение 1. Будем называть определенную на положительной полуоси непрерывную функцию осциллирующей , если она имеет на полуоси неограниченную справа последовательность нулей.

В исследовании уравнения (1) важную роль занимает его характеристическая функция

g ( Р ) = P + \ 0 e - ^{p 5 d}r ( Z ) , p ^{е С} .

Теорема 1 . Все решения уравнения (1) осциллируют тогда и только тогда , когда функция g не имеет вещественных корней .

Для доказательства теоремы 1 нам понадобятся следующие вспомогательные утверждения.

Лемма 1 [9]. Любое решение уравнения (1) при любом Хе R представимо в виде

x ( t ) = Е q m ( t ) e p m + z ( t ) , t ^{е R} + ,

Re pm >X где сумма берется по всем нулям pm функции g , для которых Re pm > X , qm - полином, степень которого на единицу меньше кратности корня pm, причем lim j (t) e~Xt = 0.

t ^+®

Рассмотрим функцию

v ( t ) = Е n = 1 R i cos ( P i^{ -ф i ) ,        ⁽²⁾

где n е N ,        R i >  0,        в i , ф i е R ,

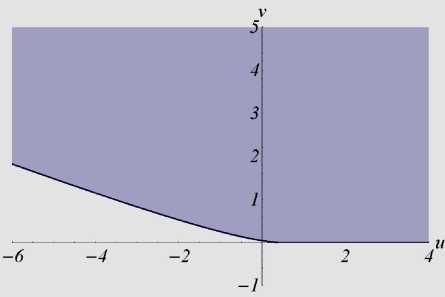
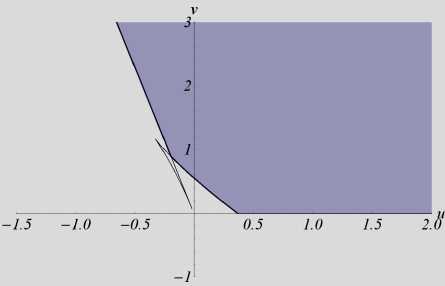
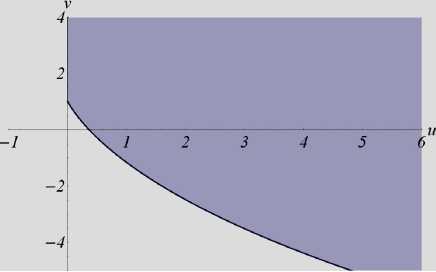
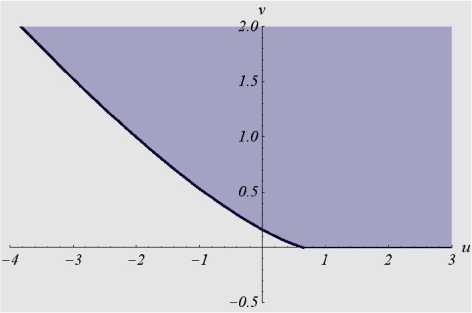
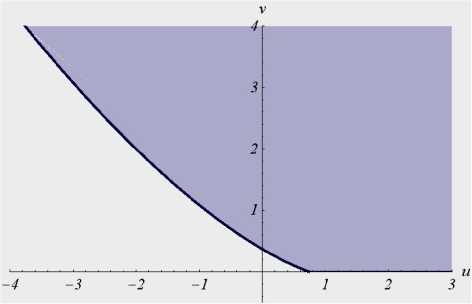
0

Лемма 2. Функция ф является осциллирующей.

Доказательство. Из теоремы Ролля следует, что между двумя нулями дифференцируемой функции лежит нуль ее производной. Значит, если бесконечно дифференцируемая функция осциллирует, то осциллирует любая ее производная.

Рассмотрим функцию nR

y⁽t ) = Е    ^{cos (e}it ^-ф0 .

i=1 ^вi

Докажем, что при некотором k е N функция y является осциллирующей.

Так как p1 <рi для любых i > 2, то можно выбрать k так, чтобы выполнялось неравенство

R1> Е Ri э4k    ^^ п4k .

’I       i=2 ^ei

Возьмем 0„ = ф1+2п n n      pi n е N . Вычислим

R nR

y (0n ) = dr+ Е лтcos(Рiеn -ф0> ₽1 i=2 в i

_R1    n _Ri

• >_R4k^Е_R4k > ⁰ ,

P1     i=2 Pi

n

y(9 n +nd- dr+ Е dr < 0.

P1     i=2 Pi

Следовательно, функция y является осциллирующей, а так как y^(4k) (t ) = ф( t), то лемма доказана. □

Доказательство теоремы 1.

Необходимость. Если функция g имеет вещественный корень Zq, то уравнение (1) имеет неосциллирующее решение e^Zqt.

Достаточность. Известно [9], что:

• а)    существует такое Xq е R, что функция g не имеет нулей при Re p > Xq ;

• б)    множество нулей функции g конечно в каждой вертикальной полосе на комплексной плоскости.

• 3.    Уравнение с двумя запаздываниями

Следовательно, количество нулей функции g с наибольшей вещественной частью конечно. Обозначим эти нули через p_i , их количество через n, Re Pi = a_max, Im Pi = вi. В силу леммы 1 любое решение уравнения (1) имеет вид

x(t) = e^amaxt Еn=1(4(t)cos (вit) +

+Bi( t)sin (в it )) + e( t), где Ai , Bi – полиномы, степени которых на единицу меньше кратности корня pi , |e(t)|< Nea0t, ao < amax . Однако ao больше вещественной части нулей функции g , находящихся слева от прямой Re p = amax.

Обозначим максимальную степень полиномов Ai, Bi, i = 1, n , через m0, а коэффициенты перед t^m0в этих полиномах – a_i и b_i соответственно. Получаем

---xt)—- = W (t ) + £ (t), tm 0 e amax t где lim £(t) = 0, w(t)=£”!aicos^it)+ bisin(Pit))• t ^tw

Очевидно, что функцию w можно привести к виду (2). Тогда по лемме 2 функция у осциллирует. Следовательно, функция x также осциллирует. □

Применим теорему 1 к исследованию осцилляции решений следующего уравнения:

x (t) + bx (t - h) + c ^__тx (s) ds = 0, t e R₊, (3) где b, c e R , h, т > 0.

Характеристическая функция уравнения (3) имеет вид:

g (P) = P + be ~ ph + c ' e_/t, p e C.

Лемма 3. Пусть при некоторых b0, c0 e R и h, т > 0, функция g 0 (P) = P + b0e -ph + c0 1-eF имеет хотя бы один вещественный корень.

Тогда для всех b, c e R таких, что b< b0, c< c0, функция g также имеет хотя бы один вещественный корень.

Доказательство. Очевидно, что при всех ZeR справедливо g(Z)<g₀(Z) • При некотором Z0 e R справедливо g0 (Z0) = 0, поэтому g (Z0) < g 0 (Z0) = 0 • С другой стороны, lim g (Z) = +w • Поэтому функция g имеет Z^+® хотя бы один вещественный корень. □

Лемма 4. Если выполнено любое из условий

• а) h > т, b< 0,

б h < т, c < 0, то функция g имеет хотя бы один вещественный корень.

Доказательство. Заметим, что lim g(Z) = +® • Помимо этого, если h >т и Z^+® b < 0 (или h <т и c < 0), то lim g (Z) = -®.

Z^-®

Поэтому функция g имеет хотя бы один вещественный корень. □

Лемма 5. Пусть h< т. Тогда для любых b e R , h, т > 0 найдется такое c0 e R₊, что для любого c > c0 функция g не имеет вещественных нулей, причем при некотором ZeR справедливо

Z + be-Z h + c 01-f = 0,1 - bhe ~Z h + c 0   1 e = 0.

d Z Z

Доказательство. Из условия g(Z) = 0

получаем c = Z+be-Zh

1-e-^•

Z

Считая c функцией от Z, продифференцируем последнее выражение по Z:

dc _ _ 1-bhe-Zh , Z+be-Zh d {l-edH dz             т f 1e-z^2 dz( z ) •

^Z I Z J

Найдем такое

Z₀ , что

dc dZ Z=Z0

dg

Учитывая g(Z0 ) = 0, получаем dZ

Z=Z0

= 0

.

Наконец, применив лемму 3, имеем ^c0 =^c(^Z0) • □

Аналогично лемме 5 доказывается сле- дующее утверждение.

Лемма 6. Пусть h > т. Тогда для любых c e R, h, т > 0 найдется такое b0 e R₊, что для любого b > b0 функция g не имеет вещественных нулей, причем при некотором Z e R справедливо

'Z + b0 e-^Zh + c ¹-e± = 0,

• 1    - b₀he ^Zh + c£ i-e-^l = 0.

• 4.    Эффективные признаки осцилляции

d Z Z

Леммы 5 и 6 указывают на необходи- мость исследования системы

C- be~C h + c — 0,   Ze R,

\                   C                         (4)

• 1 - bhe^Ch + c^ ¹e = 0. d^{C C}

Равенства (4) приводят к тому, что

_L    e^h %^Т(1+С^) e “^CZdZ _     h Z+1

• b —--77---- C —

^(Z—h)e^—CZdZ ,     1^-^h)e^—CZdZ ■

Эти равенства описывают некоторую кривую c — c (b). Исследуем ее свойства.

h

Обозначим У —~. Также введем а -положительный корень уравнения e- s — 1 - 2,                 (5)

а « 1,593624...

Случай у > 1. Для начала вычислим

„ eh-'e—CZdZ db         0

d -l„_____CZ. .12 g1 (C) ■ dc d C

—

gi^(Z)

2,

где g (C) — у | (hC +1)Z2 — h2CZ — h2)e~CZdZ , причем

dd^ —(1 + h C)J0Z2 (Z — h) e-CZ d Z.

Из леммы 4 вытекает, что если функция g не имеет вещественных корней, то b > 0. Значит, С^е[—^а, +®).

В

рассматриваемом

J0Z2 (Z — h) e4Z d Z< 0. Поэтому случае dg1(C < 0 при d C

C > —

1   dg 1(C)

h,

d C

> 0 при C < — h-. Кроме того, dC- (—h) — 0. Тогда функция g1 возрастает при C < — h , убывает при C >

—

_h , а при

C — — h" имеет максимум. Непосредственным вычислением убеждаемся, что g1 (—a)— e^ (1— Ya)(1— a) > 0, 17 а lim g1 (C) — 0.

C^+®

Следовательно, при

^Ce[^—T, ^

функция g1 положительна. Значит, dC > 0 и dC-< 0, откуда получаем, что c — c (b) при b > 0 является монотонно убывающей функцией.

Случай у < 1. Сначала исследуем уравнение |J(Z—h)e^—CZdZ — 0 .

Интегрируя левую часть этого уравнения, получаем

(1+(т—h )C+e tC( hC—1)) e—tC которое сводится к исследованию уравнения eS— 1 + 4ё .             (6)

Несложно показать, что уравнение (6) при у < 2 имеет ровно два корня (один из них равен нулю, другой отрицательный – обозначим его 02), при Y > 2 также имеет ровно два корня (один из них равен нулю, другой положительный - обозначим его 01), при у — 2 -один корень, равный нулю. С учетом этого получаем, что неравенство c > 0 выполняется лишь при следующих значениях C:

Ce[—h,01) при y< 2, Ce[—h ,0) при Y—2, Ce[—h,02) при 2

В случае, когда Y — "1, C — — h оба уравнения системы (4) совпадают и обращаются в равенство

bhe + -c^ — 1.

a( 2—a)

Далее полагаем y^^. Перепишем систему (4) (при фиксированном y< 1) в виде

be~Cy + c f e-CZdZ — —C,

‘                    ,                                 (7)

• —bye~Cy — cf Ze4ZdZ — — 1.

Считая b и c функциями от C, про- дифференцируем оба равенства по C . Имеем

f e ' !’d « = ", d|Y e “Zy + d| jo Ze “ZZ d = = b у2 e Z + c j Z2 e 'd Z.

[—h, I1), если т>2h, [—h,0), если т = 2h, db dc

Очевидно, что d- и d- не могут быть

OH

—

-1, — I, если ah <т< 2 h, h’ т ]’                             ’ одного знака, также невозможно, чтобы только одно из данных выражений обращалось в нуль. Чтобы одновременно выполнялось dZ = 0, dZ = 0 , необходимо, чтобы b у2 e Zy

+ c j Z2e KdZ = 0. Объединяя это усло- вие с системой (7), а затем, исключая b и c , получаем, что y2 (-I, +10 ) —y- 12 -12 = 0,         (8)

11   1

где 10 = j₀e d^, 11 = £-e d^, 12 = j^ e d^ ^.

Рассматривая уравнение (8) как квадратное относительно у, убеждаемся, что оно всегда имеет два вещественных решения Yj 2 (-), так как его дискриминант больше нуля:

12 (-²12 + 4-11 + 410) = 12 j (% + 2)2 e-^ d Z > 0.

Имеем две функции У = У₁₂(Z), Y1 (Z)>Y₂(Z). Исследуем случай пересечения прямой у = const с Y1 (-). Функция Y1 (Z) имеет горизонтальную асимптоту у = 1 и единственный минимум в точке Z₀~ -4,639 . Ей соответствует y₀~ 0,866. При всех у е (у₀,1) будет две точки пересечения прямой у = const с кривой у = у1 (Z). Таким образом, при у<У0 кривая c = c (b) задается монотонно убывающей функцией, при у > У0 кривая c = c (b) при c > 0 имеет одно самопересечение. Значения - = Z1 и - = Z 2 определяют

—1, если т = аh, h

(% Zi u[-2,—h ], если h<т<а h, ^—^a, +w), если т< h.

^г0 (^т,^h ) = ‘

На плоскости Ouv зададим кривую

_    e^hZ-( 2—2 e^т-+т-)

1+(т—h)-+e^т-(h-—1), .

v = —    e ■Z-2 (1+h-)    , - o

1+(т—h )Z+e^т-( hZ—1)

Определим область D0 (т, h) следующим образом. При т< h к области D0 (т, h) отнесем все точки (u, v), лежащие выше кривой Г0 (т,h), причем и > 0. При т>h к области D0 (т, h) отнесем все точки (и,v), лежащие выше кривой Г0 (т,h), причем v > 0 .

На основе изложенного выше получаем следующий результат.

Теорема 2. Все решения уравнения (3) осциллируют тогда и только тогда, когда точка (b,c) принадлежит области D0 (т, h).

На рис. 1 изображены три сечения области D₀ .

точку самопересечения, причем получающаяся "петля" лежит ниже кривой c = c (b), по- строенной при

^Ze(%^zi    -2-^-h] ^(см.

рис. 1, второй график). Часть кривой без "петли" задается монотонно убывающей функцией.

Введем

Рис. 1. Область D0 (т,h) при h = 1, т = 4 (вверху), при h = 1, т = 1.08 (в середине) и при h = 0.8, т = 1 (внизу)

Аналогично можно найти условия осцилляции решений следующих уравнений:

x(t) + bx(t - h) + cx(t - т) = 0, t g R₊, (9)

x(t) + bjtt-hx(s)ds + c^__тx(s)ds = 0, t g R₊.(10) В обоих уравнениях b, c g R , h, те R₊ . Случай h = т содержится в теореме 2, поэтому, не нарушая общности, далее считаем, что h< т .

На плоскости Ouv зададим кривую

Г1 (т, h ) =

u = 1+т eZ h, т- h

v = _ zh e^, ^Г- 1 +да).L       т-h           L h /J

.

К области D1 (т, h) отнесем все точки (u, v), лежащие выше кривой Г1 (т, h), при- чем v > 0 .

Теорема 3 [12]. Все решения уравнения (9) осциллируют тогда и только тогда, когда точка (b,c) принадлежит области Di (т, h).

На рис. 2 изображено характерное сечение области D₁ .

Рис. 2. Область Di (т, h) при h = 0,5, т = 2

На плоскости Ouv зададим кривую

Г2 (т, h) =

sezhp—H

-^h^h _h₊he^ ’

Zezт( 2 ezh -zh-2) т-тeZh-h+he’ZG[-h’H’, где a - положительный корень уравнения (5).

• К области D2 (т, h) отнесем все точки (u, v), лежащие выше кривой Г2 (т, h), причем v > 0 .

• 5. Некоторые следствия

Теорема 3. Все решения уравнения (10) осциллируют тогда и только тогда, когда точка (b,c) принадлежит области D2 (т,h).

На рис. 3 изображено характерное сечение области D₂ .

Рис. 3. Область D2 (т,h) при h = 1, т = 2

Сформулируем несколько легко проверяемых достаточных признаков осцилляции.

Следствие 1 [6]. Пусть b,c g R + и bh + cт >1.

e

Тогда все решения уравнения (9) осциллируют.

Пусть а - положительный корень уравнения (5). Обозначим k = а(2 - а). Тогда k « 0,64761...

Следствие 2. Пусть b, c е R+ и bh²+ cт²> k .

Тогда все решения уравнения (10) осциллируют.

Следствие 3. Пусть b, c е R+ и bhe + cT2 > 1 k

Тогда все решения уравнения (3) осциллируют.

Заметим, что признак осцилляции, сформулированный в следствии 3, является точным: при Т = а он является критерием осцилляции всех решений уравнения (3).