Об участии в работе тонкой гофрированной стенки стального двутавра на продольные усилия
Автор: Степаненко А.Н., Тишков Н.Л.
Журнал: Вестник Восточно-Сибирского государственного университета технологий и управления @vestnik-esstu
Рубрика: Технические науки
Статья в выпуске: 4 (61), 2016 года.
Бесплатный доступ
В статье рассмотрена и уточнена работа тонкой гофрированной стенки стального двутавра на продольные усилия, возникающие в изгибаемых элементах. Для оценки относительной величины зоны тонкой гофрированной стенки с треугольным профилем гофров, работающей совместно с поясами на продольные усилия, выполнен численный эксперимент в программном комплексе ЛИРА-САПР. Произведен математический анализ напряженно-деформированного состояния 75 гофрированных балок, в результате чего получены максимальные и минимальные значения участков гофрированной стенки, работающей совместно с поясами балок, получены дробно-степенные регрессии.
Балка, гофрированная стенка, треугольный профиль гофра, поверхность стенки, математический анализ
Короткий адрес: https://sciup.org/142143235
IDR: 142143235 | УДК: 624.074.421
Текст научной статьи Об участии в работе тонкой гофрированной стенки стального двутавра на продольные усилия
При определении положения центра тяжести приведенного сечения пояса двутаврового стержня с непрерывно гофрированной тонкой стенкой в [1] предлагается учитывать в совместной работе с ним на нормальные усилия половину сечения стенки при возможных параметрах гофров в ней.
В действительности совместно с каждым поясом в большинстве случаев работает только небольшая часть стенки (0,1…0,3 ее высоты), и только при длине полуволны гофра ( S ) больше высоты сечения стенки ( h ) на нормальные усилия работает вся стенка (с вогнутыми эпюрами напряжений). Установлено также, что гофрированная стенка стального двутавра работает аналогично плоской в комбинированной конструкции (например, если двутавр расположен в железобетонной плите или колонне).
Методы исследования
Для приближенной оценки относительной величины зоны тонкой гофрированной стенки с треугольным профилем гофров, работающей совместно с поясами на продольные усилия, выполнен численный эксперимент на 75-ти гофрированных балках длиной 7200 мм.
С использованием МКЭ получены картины распределения нормальных напряжений ( J x ) по длине и высоте их стенок с пятью размерами гофров s х f (рис. 1): 450x90, 225x90,
150х90, 150х60 и 150х30 мм. Размеры сечений элементов опытных балок представлены в таблице 1.
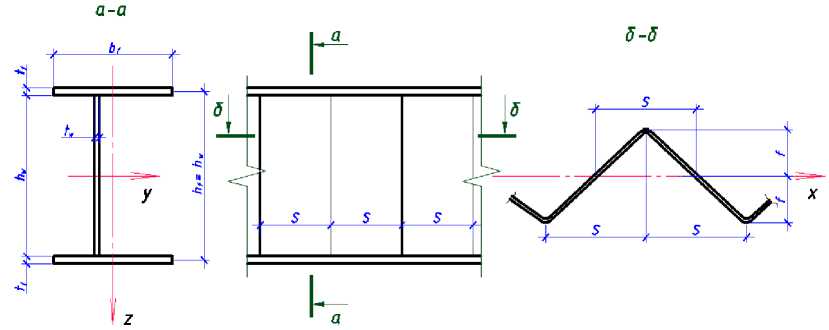
Рисунок 1 – Схема поперечного сечения опытных образцов и профиля гофров их стенок
Длина пластинчатых КЭ стенок и поясов всех образцов принята равной s /4, ширина конечных элементов стенок (КЭ41) - hw / 20 при hw = 720 мм и hw / 10 при h 560 и 360 мм.
Таблица 1
Размеры сечений элементов опытных балок
|
hw ⋅ t w |
bf ⋅ tf |
||||
|
369 x 9 |
270 x 9 |
180 x 9 |
180 x 6 |
180 x 4,5 |
|
|
720 x 3,6 |
+ |
+ |
+ |
||
|
720 x 2,4 |
+ |
+ |
+ |
||
|
720 x 1,8 |
+ |
+ |
+ |
||
|
560 x 1,8 |
+ |
+ |
+ |
||
|
360 x 1,8 |
+ |
+ |
+ |
||
Все опытные образцы нагружались поперечной равномерно распределенной по верхнему поясу нормативной погонной нагрузкой как наиболее часто встречающейся в изгибаемых элементах зданий и сооружений.
Результаты исследования
Фрагмент изополей нормальных (продольных) напряжений в стенке опытной балки (с размерами: hw ⋅ tw = 720 ⋅ 2.4; bf ⋅ tf = 720 ⋅ 2.4и S ⋅ f = 225 ⋅ 90 ), полученный с использованием Программного комплекса ЛИРА-САПР, приведен на рисунке 2.
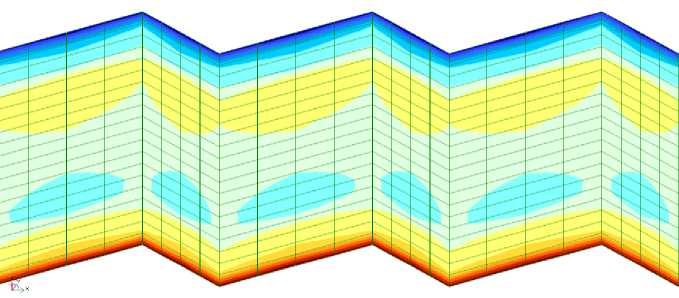
Рисунок 2 – Изополя нормальных напряжений фрагмента гофрированной стенки (13,5 ⋅ S ≤ x ≤ 19,5 ⋅ S ) опытной балки
Эпюры нормальных напряжений для 4-х характерных поперечных сечений стенки этой балки (по вершинам 2-х гофров и по серединам смежных с ними граней гофров, расположенных ближе к опоре балки и к середине ее длины) приведены в таблице 2.
Таблица 2
Эпюры нормальных напряжений в поперечных сечениях стенки балки с размерами: h w • t w = 720 • 2.4 ; b f • t f = 720 • 2.4 и 5 • f = 225 • 90
|
Сечения по граням гофров при расстоянии от опоры |
Сечения по вершинам гофров при расстоянии от опоры |
|||||
|
x = 3 ■ 5 |
x = 16 ■ 5 |
x = 3,5 • 5 |
x = 16,5 • 5 |
|||
|
.1МП |
"Эл |
|||||
По картинам изополей и эпюрам нормальных напряжений в поперечных сечениях стенок для всех опытных балок определены размеры участков стенок, «работающих совместно с поясами» ( cW - у верхнего и cW - у нижнего поясов) (рис. 3).
6 8
С w
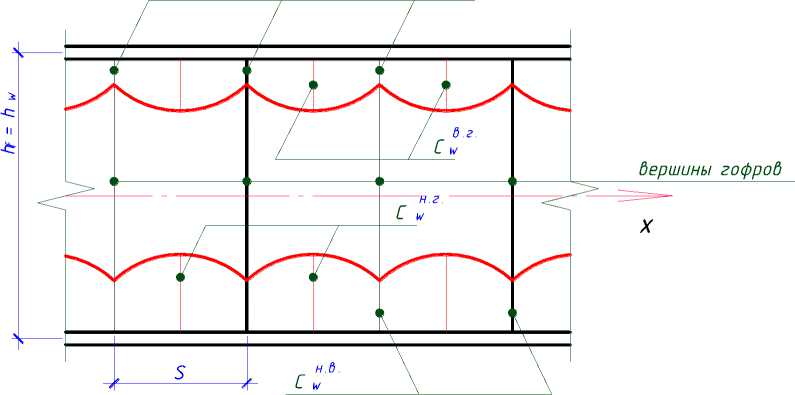
Рисунок 3 - Схема размеров участков стенки гофрированной балки, работающих совместно с поясами
При этом установлено, что размеры этих участков не зависят от величины o x (при о у * 0 ), всегда переменные в пределах ширины грани гофра (с максимумами у середин граней и минимумами на вершинах гофров) (рис. 3, табл. 3), а размер этих участков у верхних поясов опытных балок в большинстве случаев меньше, чем у нижнего пояса (иногда до 20 %). При других схемах нагружения гофрированного двутавра (осевое сжатие, чистый изгиб, сосредоточенная поперечная сила) припоясные участки стенки, работающие с поясами, симметричны.
Таблица 3
Относительная высота участков гофрированной стенки, работающая совместно с ее поясами
|
b f *t f |
s*f |
h*t w = 720 * 3,6 |
h*t w = 720 * 2,4 |
h*t w = 720 * 1,8 |
|||||||||
|
У вер го |
шины ра |
По грани гофра |
У вершины гофра |
По грани гофра |
У вершины гофра |
По грани гофра |
|||||||
|
в . в c w |
н . в c w |
c wв . г |
н . г c w |
в . в c w |
н . в c w |
c wв . г |
н . г c w |
в . в c w |
н . в c w |
c wв . г |
н . г cw |
||
|
360*9 |
450*90 |
0,26 |
0,285 |
0,29 |
0,33 |
0,25 |
0,29 |
0,28 |
0,34 |
0,25 |
0,29 |
0,28 |
0,34 |
|
225*90 |
0,145 |
0,14 |
0,16 |
0,18 |
0,14 |
0,155 |
0,15 |
0,185 |
0,14 |
0,16 |
0,14 |
0,19 |
|
|
180*90 |
0,10 |
0,12 |
0,12 |
0,14 |
0,10 |
0,115 |
0,115 |
0,14 |
0,10 |
0,12 |
0,10 |
0,15 |
|
|
180*60 |
0,10 |
0,11 |
0,125 |
0,14 |
0,10 |
0,12 |
0,12 |
0,14 |
0,10 |
0,11 |
0,12 |
0,14 |
|
|
180*30 |
0,10 |
0,10 |
0,125 |
0,13 |
0,10 |
0,10 |
0,12 |
0,135 |
0,10 |
0,11 |
0,12 |
0,13 |
|
|
270*9 |
450*90 |
0,25 |
0,28 |
0,30 |
0,33 |
0,25 |
0,285 |
0,29 |
0,335 |
0,25 |
0,28 |
0,28 |
0,33 |
|
225*90 |
0,15 |
0,185 |
0,17 |
0,18 |
0,14 |
0,155 |
0,16 |
0,19 |
0,14 |
0,15 |
0,15 |
0,18 |
|
|
180*90 |
0,10 |
0,12 |
0,12 |
0,14 |
0,11 |
0,115 |
0,12 |
0,145 |
0,10 |
0,11 |
0,11 |
0,15 |
|
|
180*60 |
0,10 |
0,11 |
0,13 |
0,13 |
0,10 |
0,10 |
0,13 |
0,135 |
0,10 |
0,10 |
0,12 |
0,14 |
|
|
180*30 |
0,10 |
0,10 |
0,13 |
0,13 |
0,10 |
0,10 |
0,135 |
0,135 |
0,10 |
0,10 |
0,13 |
0,14 |
|
|
180*9 |
450*90 |
0,27 |
0,28 |
0,31 |
0,33 |
0,27 |
0,29 |
0,30 |
0,34 |
0,26 |
0,30 |
0,29 |
0,33 |
|
225*90 |
0,15 |
0,155 |
0,17 |
0,18 |
0,15 |
0,155 |
0,165 |
0,185 |
0,15 |
0,16 |
0,16 |
0,18 |
|
|
180*90 |
0,10 |
0,11 |
0,135 |
0,14 |
0,13 |
0,135 |
0,12 |
0,14 |
0,10 |
0,12 |
0,12 |
0,15 |
|
|
180*60 |
0,10 |
0,11 |
0,125 |
0,13 |
0,10 |
0,12 |
0,12 |
0,14 |
0,10 |
0,11 |
0,13 |
0,13 |
|
|
180*30 |
0,10 |
0,11 |
0,13 |
0,13 |
0,10 |
0,10 |
0,125 |
0,135 |
0,10 |
0,10 |
0,12 |
0,13 |
|
|
180*6 |
450*90 |
0,25 |
0,28 |
0,28 |
0,33 |
0,39 |
0,42 |
0,45 |
0,50 |
0,48 |
0,49 |
0,48 |
0,50 |
|
225*90 |
0,14 |
0,15 |
0,15 |
0,18 |
0,20 |
0,20 |
0,25 |
0,26 |
0,34 |
0,37 |
0,39 |
0,44 |
|
|
180*90 |
0,10 |
0,11 |
0,11 |
0,15 |
0,18 |
0,18 |
0,18 |
0,20 |
0,23 |
0,24 |
0,28 |
0,29 |
|
|
180*60 |
0,10 |
0,10 |
0,12 |
0,14 |
0,18 |
0,18 |
0,18 |
0,18 |
0,20 |
0,21 |
0,26 |
0,27 |
|
|
180*30 |
0,10 |
0,10 |
0,13 |
0,14 |
0,19 |
0,19 |
0,19 |
0,19 |
0,20 |
0,20 |
0,25 |
0,26 |
|
|
180*4,5 |
450*90 |
0,26 |
0,30 |
0,29 |
0,33 |
0,39 |
0,42 |
0,46 |
0,50 |
0,48 |
0,49 |
0,48 |
0,50 |
|
225*90 |
0,15 |
0,16 |
0,16 |
0,18 |
0,20 |
0,20 |
0,26 |
0,27 |
0,33 |
0,33 |
0,39 |
0,43 |
|
|
180*90 |
0,10 |
0,12 |
0,12 |
0,15 |
0,19 |
0,19 |
0,19 |
0,19 |
0,23 |
0,23 |
0,28 |
0,29 |
|
|
180*60 |
0,10 |
0,11 |
0,13 |
0,13 |
0,18 |
0,18 |
0,19 |
0,19 |
0,20 |
0,20 |
0,26 |
0,27 |
|
|
180*30 |
0,10 |
0,10 |
0,12 |
0,13 |
0,18 |
0,18 |
0,19 |
0,19 |
0,19 |
0,19 |
0,25 |
0,25 |
|
Так как величина размера участка стенки, работающей совместно с поясом, зависит от всех размеров сечения стержня и размеров гофров, то наиболее приемлемым приближением (с точки зрения количества определяемых коэффициентов регрессии) представляется множественная дробно-степенная регрессия [2]. Ее можно представить в виде cw = a1'
hw
a 2
a
s
V f 7
( b
a 4
V s 7
I f Г
V f 7
, A a 6 hw bf
hw
a 7
V f 7
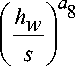
где cw - опытное значение определяемой величины; ai - коэффициенты регрессии.
Линеаризуя регрессию логарифмированием, можно получить неоднородное линейное уравнение
Г, к 7 к (ьА (ьА h 5 ft ft
1g ( cw ) = g( ( a 1) + a 2• , g -w + a 3 g a4 tg -+ ... f +
t
к 5 7
к
h
+a6 • ^ Tw bf
h
+ а 7 • g -^
h
+ a8 • ^ I — к 5
с неизвестными коэффициентами b = g(a1) , a2....a8 , которые можно найти методом наименьших квадратов из решения переопределенной системы уравнений (75 х 8), составленной из опытов для перечисленных в таблице 1 уровней параметров влияния с использованием средств Mathcad. В рассматриваемом опыте определено 4 характерных размера cwi (см. рис. 3), необходимых для непрерывного описания искомой величины в произвольном поперечном сечении стенки (при тy « 0), которые можно представить для большей части длины опытных балок (hw < x < L — hw ) в виде:
в в.в в.г в.в cwx = cw + (cw — cw )• I cos(n • x / S) I — для верхней зоны стенки;
н н.в н.г н.в cwx = cw + (cw — cw )• | cos (П • x / S ) | — для нижнеи зоны стенки.
Максимальные (по граням) и минимальные (по вершинам гофров) значения размеров участков гофрированной стенки (рис. 3), работающих совместно с поясами в балках с размерами, близкими к приведенным в таблице 1, можно оценить условиями, полученными из решения переопределенной системы уравнений:
0,79 0,070,04
в.в f cwx 0,576 0,88 0,02 - 0,5;
hwb^f
0,780,19
c w.X = i,28—-097^- - 0,5;
hw ,
0,780,11
н.в cwx 0,44 0,03 0,85 0,01 - o,5;
tw *hw *bf н.г cwx
= 0,65 -
0,02 0,74 0,08 0,06
t w -S V • b f
0,90 hw
- 0,5.
Достоверность предлагаемых оценочных условий проверяется рекомендациями, предложенными в [3].
Список литературы Об участии в работе тонкой гофрированной стенки стального двутавра на продольные усилия
- Степаненко А.Н. Стальные двутавровые стержни с волнистой стенкой. -Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2001. -178 с.
- Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. -М.: Наука, 1970. -432 с.
- Ахназарова С.Л., Кафаров В.В. Оптимизация эксперимента в химической технологии. -М.: Высшая школа, 1978. -319 с.


