Область устойчивости в пространстве параметров рекурсивных нейронных сетей с топологией многомерного куба

Мы рассматриваем нейронные сети с топологией многомерного куба с одинаковыми запаздываниями во взаимодействии между нейронами в сети. Такие модели сетей используются при построении многопроцессорных вычислительных систем суперкомпьютеров [1].

Сеть с топологией n -мерного куба образуют нейроны с метками, являющимися n -мерными векторами компоненты, которых либо 0, либо 1. Два нейрона сети связаны тогда и только тогда, когда их метки отличаются только одной координатой. Связи для трехмерной сети изображены на рис. 1.

В результате линеаризации вокруг стационарного решения уравнений нейронной сети с топологией n -мерного куба получается линейное матричное разностное уравнение

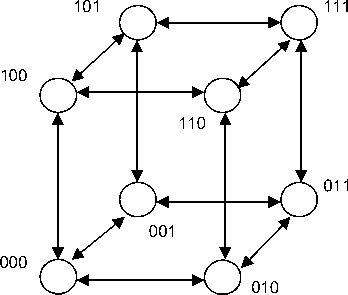
Рис. 1. Нейронная сеть с топологией трехмерного куба

xs = YIxs-1 + Qnxs-k, s = 1,2. , где xs – вектор сигналов нейронов в момент s . Вектор xs размерности 2n характеризует отклонения сигналов нейронов от стационарных, I - единичная 2n x 2n матрица, /(-1 < у < 1) - коэффициент затухания колебаний нейронов, Qn - матрица размера 2n x 2n, характеризующая взаимодействия между нейронами в сети, k – запаздывание во взаимодействии между нейронами.

Уравнение (1) принадлежит классу матричных разностных уравнений вида:

x. = Ax„ , + Bx„ k, s = 1,2..., s        s—1        s — к которые обладают важным для нас свойством: матрицы A,B могут быть приведены к треугольному виду одним преобразованием. Поэтому мы имеем возможность применить метод конуса устойчивости [7] для устойчивости этих уравнений.

Пусть z0 и z1 – метки связанных между собой нейронов, и одна из координат z0 равна 0, в то время как соответствующая координата метки z1 равна 1. Обозначим силу воздействия нейро- на с меткой z0 на нейрон с меткой z1 посредством a , а силу обратного воздействия посредством

• b . Тогда блочная 2 n x 2 n матрица Q n в (1) определяется рекуррентно равенствами:

  Q 1 =

  
  

  0 b

  I

  V a 0 )

  
  

  Q n =

  
  

  '^Qn.■ al

  
  

  bI

  Q n - 1

  
  
  
  

Краткие сообщения

Мы ставим задачу изучить область устойчивости системы (1) в пространстве параметров γ , a , b , k при разных значениях n .

Конус устойчивости для диагностирования устойчивости нейронных сетей

В работах [7, 8] введены конусы устойчивости для диагностирования устойчивости систем вида (2) с матрицами A , B , одновременно приводимыми к треугольному виду. Аналогичные конусы устойчивости для дифференциальных уравнений введены в [9]. Для решения задачи устойчивости нейронных сетей с топологией связей n -мерного куба нам понадобится техника конусов устойчивости, которую мы здесь изложим.

Определение 1. Конусом устойчивости для уравнения вида (2) для данного k мы называем множество точек M = (u1,u2,u3)∈ R3 , такое что u1 +iu2 = exp(ikω) - hexp(i(k -1)ω), u3 = h,(4)

где параметры h , ω связаны соотношениями:

sin kω   ππ

0 ≤ h ≤           ,- ≤ ω≤ .(5)

sin(k - 1)ω kk

Теорема 1 [7]. Пусть A,B,S ∈ R2n×2n и S-1AS = AT,S-1BS = BT , где AT ,BT – треугольные матрицы с диагональными элементами λj,µj соответственно (1 ≤ j ≤ 2n) . Построим точки M = (u1,u2,u3)∈ R3 (1 ≤ j ≤ 2n) так, что u1j + iu2j = µj exp(-ik argλj), u3j = λj .(6)

Тогда уравнение (2) асимптотически устойчиво, если и только если все точки M_j лежат внутри конуса устойчивости (4), (6) для данного k . Если некоторая точка M _j лежит вне конуса устойчивости, то уравнение (2) неустойчиво.

Теорема 1 сводит задачу диагностирования устойчивости системы (2) порядка (2 ⁿ × 2 ⁿ ) к геометрической задаче в R 3 : асимптотическая устойчивость системы равносильна условию, что все точки M_j (1 ≤ j ≤ 2 ⁿ ) лежат внутри конуса устойчивости (4), (6) для данного k .

Собственные значения матрицы Qn

Теорема 2. Собственные числа µnj (1 ≤ j ≤ 2n) матрицы Qn удовлетворяют рекуррентному соотношению где µ11

= ab , µ ₁₂ = - ab .

^ n + 1,j = 1

µ _nj + ab , если 1 ≤ j ≤ 2 ⁿ

X^ nj

- ab , если 2 ⁿ + 1 ≤ j ≤ 2 ^{n + 1}

Доказательство. Очевидно, µ11 = ab , µ12 = - ab . Ввиду (3) характеристический много- член fn (µ) для (1) имеет вид fn(µ)=det((µI-Qn-1)2-abI).

Из (7), (8) следует fn+1(µ) =det((µI-Qn)2 -abI) =det(Qn -I(µ- ab)) det(Qn -I(µ+ ab)).

Ввиду (9) уравнение  fn+1(µ) = 0 распадается на два уравнения:  fn(µ- ab) = 0 , fn (µ+ ab) = 0 . Теорема 2 доказана.

Диагностирование устойчивости сети с топологией многомерного куба

Определение 2. Овалом устойчивости для уравнений вида (2), для запаздывания k > 1 и параметра γ мы называем кривую M(ω) = (u1(ω), u2(ω)) такую, что u1(ω) + iu2(ω) = exp(ikω) - γ exp(i(k -1)ω) ,

Иванов С.А.                                  Устойчивость рекурсивных нейронных сетей с топологией многомерного куба где toe (-to1,to1~), to1 - есть наименьший положительный корень уравнения sin kto

।Y = sin( k - 1)to "

Овал устойчивости для данного запаздывания k и данного γ – это сечение конуса устойчивости (см. определение 1) плоскостью и 3 = Y . Овалы устойчивости при 0 <  у <  1 рассматривала Е. Каслик [4]. Благодаря теоремам 1, 2 для диагностирования устойчивости уравнения (1) достаточно проверить одну точку M ( и 1 , и 2 ) = и 1 + iu 2 = n4ab . Поэтому имеют место следующие теоремы.

Теорема 3. Пусть даны произвольные n, k e Z+, к > 1. Пусть 0 < у < 1. Построим в R2 овал устойчивости (см. определение 2) для данных к,у. Построим точкуM = (и1,и2)e R2 так, что и1 + iu 2 = n~Jab sin to(y) cos(к - 1)to(y),

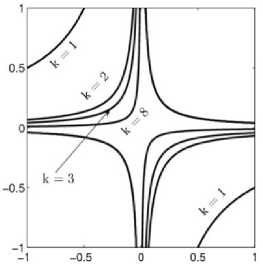
Рис. 2. Область устойчивости системы (1) в плоскости ( a , b ) при фиксированных

Y = 0,4, n = 3 и переменном запаздывании k

Если точка M лежит внутри овала устойчивости, то система (1) асимптотически устойчива. В противном случае система (1) неустойчива.

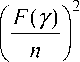
то

Теорема 4 . Если 0 <  ab <

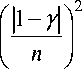
или 0>ab> система (1) асимптотически устойчива. Здесь F(у) = где to(y) есть наименьший неотрицательный корень уравнения

। । = sin kto cos( k - 1)to

Если число ab находится вне границ указанных интервалов, то система (1) неустойчива.

Области устойчивости системы (1) отражены на рис. 2.