Обобщение модели эмоционального воспитания
Автор: Пенский Олег Геннадьевич, Черников Кирилл Викторович
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 2 (2), 2010 года.
Бесплатный доступ
Доказана общая теорема о стремлении к постоянной величине значения воспитания забывчивого субъекта при непрерывном воспитательном процессе. Предложены безразмерные функции, определяющие эмоциональную память индивидуума.
Эмоции, воспитание, математическая модель
Короткий адрес: https://sciup.org/14729658
IDR: 14729658 | УДК: 519.86;
Текст научной статьи Обобщение модели эмоционального воспитания
В работах [1, 2] предложена формула эмоционального воспитания забывчивого субъекта, которая имеет вид
R ( t ) = r ( т ) + 0 i r i - 1 + 0.0 .— г - 2 +
+ &№ - 2 r - 3 + ... + 000 2 .. 0 1 Г о , ( )
где 0i - безразмерные коэффициенты памяти, зависящие от времени, 0 < 0 < 1, rj - эле ментарные воспитания, j = 1, i, j - порядко-tj вый номер такта [1], r = jМ}(т)dr, tj -0
полное время действия на субъекта эмоции
Mj (t), t - время, т - текущее время дейст- вия последней эмоции.
Известно [1], что элементарные воспитания удовлетворяют неравенству
I rj|< q.(2)
При стремлении значения i к бесконечности соотношение (1) примет вид
ж
R = S ri—i n Oj.(3)
i=i
Теорема. Ряд (3) сходится.
Доказательство. Покажем, что ряд (2) сходится абсолютно.
Так как выполняется неравенство 0 < 0 < 1, то существует такое 0 меньшее
единицы, что справедливо соотношение
0 i < 0 < 1, где i = 1, ж .
В силу неравенства (2), формулы (3) и равенства для определения суммы членов геометрической прогрессии [3] можно записать соотношение ж i —1 ж
S i r —.| П 0 j < S q 0 = -A.
i = 1 j = 1 i = 0 1 — 0
Таким образом, ряд (3) сходится абсолютно и, следовательно, он сходится [4].
Теорема доказана.
Следствие. Воспитание забывчивого субъекта, соответствующее концу тактов, стремится к постоянной величине воспитания при бесконечном увеличении времени непрерывного воспитательного процесса.
Доказательство. Так как ряд (3) сходится, то при увеличении времени непрерывного воспитательного процесса ( i ^ ж ) воспитание субъекта, соответствующее концу тактов, будет стремиться к постоянной величине.
Таким образом, следствие доказано.
Оценим величину погрешности воспи- тания при условии, когда для оценки суммы ряда (3) применяется k членов ряда.
Очевидно, что погрешность bk+1
ж i — 1
У r п 0, ij i=k+1 j
при конечном суммирова-
нии k членов ряда (3) будет удовлетворять
Определение 1. Обобщенной функцией
неравенству
ь < q^-к +1 i - в
•
Согласно работе [1], формула (3) определяет воспитание при непрерывном воздействии на субъекта эмоциями. Но легко видеть, что в конце полных воспитательных циклов [1], количество которых равно n , общая функ- [ n ]
ция воспитательного процесса V, . , опреде- ln ,in
ляющая воспитание, полученное в результате этих циклов, удовлетворяет соотношению
V [ p ] =
1 p , i p
( i p - [ p ] Y
П в к к = 1
V
7_
[ p ] r i p + 1
i p + 1 к (i p
p xVr[p] П f[p] x Tp p]TZ[p-1]
+ / Гк-П‘ в + пц у, к 1 j=i J i=i i lp -i> ip - k=1 V
p
l p - 1 > i p - 1
p = 2, n ,
V[1] = i1, l1
< l 1
- [1П
П в к к = 1
V
' 1 + 1 к
^+ Z r - 1 п в 1] ,
к = 1
J = 1
где [ i ] - обозначение переменных, соответст-
вующих воспитательному циклу с номером i , - - [p]
i = 1 ,n , в к соответствует тактам без эмоциональных воспитаний цикла с номером p , к - номер такта без эмоциональных воспитаний, l p - количество тактов цикла с номером p без
эмоциональных воздействий, i p - количество тактов воспитательного цикла с номером p при непрерывных эмоциональных воспитательных воздействиях.
Очевидно, что для забывчивого субъекта [1] справедливы неравенства
I V pi p К F ■ i p
F lp, ip
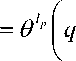
1 - в
+ вpFl
p - 1 , i p - 1
p = 2, n ,
I V [1 ]\ < Ft ; , F t = q ^ i —, I l 1 , i 1 I l 1 , i 1 1 1 , i 1 1 у в
= [ p ]
где в = max( в j , в}p ] ),
i = 1, ip , J = 1, i p , p = 1, n • Введем несколько определений.
памяти W1 n.] назовем величину, удовлетво- ln,in
-[n] Vin ряющую соотношению W i i = —n,n-q
Определение 2. Обобщенным индика-
тором пресыщения воспитания назовем функ-
IV l[n] l ( 1 - в ) цию вида W,["] = ——------ n , n nq
•
Исходя из вышеприведенных определений, следует, что обобщенная функция памяти и обобщенный индикатор пресыщения воспитания являются безразмерными функциями.
Очевидно, что обобщенный индикатор пресыщения воспитания удовлетворяет неравенству 0 < W[n] < 1. Так же легко видеть, ln ,in что для равномерно забывчивого субъекта с равноценными эмоциями обобщенная функция памяти эквивалентна функции памяти, обобщенный индикатор пресыщения воспитания эквивалентен индикатору пресыщения воспитания [1].
В настоящее время авторами публикации разрабатывается компьютерная программа моделирования поведения эмоционального робота, алгоритм которой основан на вышеприведенных обобщенных моделях эмоционального воспитания субъекта. Программа будет моделировать эмоции робота, возникающие в результате звуковых раздражителей.
Список литературы Обобщение модели эмоционального воспитания
- Пенский О.Г., Зонова П.О., Муравьев А.Н. и др. Гипотезы и алгоритмы математической теории исчисления эмоций. Под общ. ред. О.Г.Пенского/Перм. ун-т. Пермь, 2009. 152 с.
- Пенский О.Г. Математические модели эмоционального воспитания//Вестн. Перм. ун-та. Математика. Механика. Информатика/Перм. ун-т. Пермь, 2009. Вып. 7(33). С.57-60.
- Самарский А.А., Михайлов А.П. Математическое моделирование. М.: Физматлит, 2005. 320 с.
- Кудрявцев Л.Д. Краткий курс математического анализа. М.: Физматлиз, 2002.400 с.


