Обоснование гипотезы Сазерленда — Эйнштейна для магнитных полей астрофизических объектов в рамках геометрического подхода

В ряде своих работ (1900-1908 гг.) Сазерленд [1–4] предположил следующую модель магнитного поля Земли. Первичное поле обусловлено вращением поверхностного (отрицательного) и объемного (положительного) зарядов. При этом заряды компенсируют друг друга, то есть, скомпенсированы создаваемые ими электрические поля, но не магнитные. Поэтому мы и не можем

Работа выполнена при поддержке программы 10 «Экспериментальная лабораторная астрофизика и геофизика» Национального центра физики и математики.

• ¹    E-mail: inna.babenko@list.ru

• ²    E-mail: zhilkin@inasan.ru

наблюдать сильных электрических полей. Но при этом он отмечал, что наличие внешнего магнитного поля, как раз и является доказательством сильного внутреннего электрического поля.

В 1925 году Эйнштейн (неизвестно был ли он знаком с работами Сазерленда) [5] высказал предположение об очень малом (вне пределов разрешимости современной аппаратурой) различии значений зарядов тяжелых положительно заряженных и легких отрицательно заряженных частиц. Это приводит к возникновению избытка заряда у достаточно массивных астрофизических объектов, для которых объемный положительный заряд, кулоновское поле которого компенсируется редуцируемыми отрицательными частицами. А вращение астрофизических объектов приводит к генерации наблюдаемого дипольного магнитного поля.

Но в 1925 году А. Piccard и E. Kessler показали [6], что значения зарядов протона и электрона одинаковы до 20 знака (1О ^-20 ) и тем самым поставили под сомнение гипотезу Эйнштейна, которая в итоге стала не актуальной и была забыта. На данный момент экспериментально подтверждается сохранение зарядов протона и электрона до 21 знака (10 ^-21 ) [7].

Гипотеза Сазерленда-Эйнштейна в свое время обладала рядом моментов, которые требовали объяснения и доработки, но в рамках сложившихся физических концепций не могли быть объяснены. Однако, различия положительно и отрицательно заряженных частиц возможно в рамках геометрической физической концепции [8].

Основу геометрического подхода составляет общая теория относительности и ее обобщения в виде многомерных геометрических моделей (типа Калуцы или Клейна, теорий с кручением, с сегментарной кривизной и др.), в которых поля-переносчики геометризуются, то есть трактуются как проявление геометрии искривленного пространственного-временного многообразия подходящей топологии размерности.

К идее малой зарядовой асимметрии и предлагаемому на этой основе объяснению магнитных полей астрофизических объектов можно было прийти на рубеже 20-х – 30-х годов в рамках многомерных геометрических моделей физических взаимодействий, где физические поля, в частности, электромагнитное, описываются смешанными компонентами многомерного метрического тензора Gµα . Здесь индекс µ пробегает 4 значения: 0, 1, 2, 3, а индекс α может принимать значения: 4, 5, .... Соответствующие полям заряды, в частности, электромагнитный, описываются через цик лическую зависимость волновых функций заряженных частиц от 5-й или иных дополнительных координат. Анализ показывает, что в рамках общего термина «5-мерная теория Калуцы-Клейна» можно говорить о двух различных теориях, имеющие дело с разными дополнительными размерностями и описывающие разные стороны физической реальности: геометризацию электромагнитных взаимодействий («вариант Калуцы») и геометризацию масс («вариант Клейна») [6].

Синтез теории Калуцы и Клейна можно осуществить в рамках 6-мерной геометрической модели с двумя дополнительными координатами: x ⁴ и x ⁵ . Волновые функции частиц зависят от двух координат. В данной модели редукция на 4-мерное пространственно-временное сечение осуществляется с помощью диадного метода (1+1+4 - расщепления) в калибровке типа дважды хронометрической, введенной в ОТО. Взаимодействие частиц описывается посредством диадного оператора 4-мерного дифференцирования, инвариантного при преобразованиях двух дополнительных координат и ковариантного относительно 4-мерных преобразований, где одна из комбинаций оператора отождествляется с векторным потенциалом электромагнитного поля. При этом появляется еще одна дополнительная комбинация, которая также должна быть отождествлена с векторным потенциалом электромагнитного поля. И тогда одно из слагаемых в диадном операторе приводит к чрезвычайно малым поправкам к электромагнитному взаимодействию из-за того, что возникающий при дифференцировании по x ⁴ заряд (масса) на много порядков меньше электромагнитного заряда. В рамках многомерных геометрических моделей можно найти, что масса индуцирует дополнительный (“массовый”) электрический заряд Aq = 2\/Gm).

Учитывая, что, например, для электрона масса me ^ 9, 1 • 10-28 г, получаем для него отношение дополнительного заряда к основному q/q 三 e/e ^ 10-21. Очевидно, что такая поправка в электромагнитное взаимодействие частиц лежит далеко за пределами точности эксперимента. Однако, для больших электрически квазинейтральных масс, когда электрические заряды частиц двух знаков в среднем компенсируются, ”массовый вклад” в электромагнитное взаимодействие, обусловленный квадратичным по зарядам слагаемым, может оказаться существенным [9].

Это значит, что для описания пространства-времени вокруг статических сферически симметричных объектов (в идеальном случае) следует вместо метрики Шварцшильда использовать метрику типа Рейсснера-Нордстрема. Соответственно, для вращающихся идеализированных объектов пространство-время должно описываться не метрикой Керра, а метрикой типа Керра-Ньюмена, где дополнительная константа (электрический заряд) выражается через значение масс частиц. Добавки к общерелятивистским эффектам окажутся довольно незначительными. Однако вокруг таких объектов должны возникать как электрическое, так и магнитное поля. Как известно, дипольный магнитный момент µ KN источника Керра–Ньюмена определяется формулой µ KN = qa где q — электрический заряд источника, а a — момент импульса источника. Полагая источник шаром и подставляя значение q , выражение для дипольного магнитного момента такого идеализированного объекта можно переписать в виде

µ KN ^≡ µ GR

4 GmR2Ω, 5c

где m — масса, R — радиус, Ω — угловая скорость источника [10].

Поэтому, если рассматривать астрофизические объекты, как абсолютно твердые и идеально проводящие тела, то у подобных объектов дополнительный (объемный) электрический заряд будет компенсироваться абсорбированными (поверхностными или приповерхностными) зарядами противоположного заряда, так что результирующее электрическое поле будет отсутствовать, однако в общем случае это не означает, что магнитное поле также будет скомпенсировано. Вокруг таких объектов следует ожидать некоторое эффективное магнитное поле, слагающееся из двух частей: 1) из первичного магнитного поля (1) дополнительного электрического заряда, обусловленного массой, и 2) вторичного магнитного поля, создаваемого поверхностными зарядами. Причем, данные магнитные поля являются дипольными и могут частично компенсировать друг друга. Но для реальных астрофизических тел свойственно наличие объемных наведенных зарядов и токов вращения. В итоге результирующее магнитное поле зависит от распределения поверхностных зарядов. При этом получается, что магнитные поля у астрофизических объектов отсутствуют, если эти два магнитных поля полностью компенсируют друг друга. Но если эти два поля компенсируют друг друга лишь частично, то астрофизические объекты обладают магнитными полями разной напряженности в зависимости от физических и химических условий, влияющих на распределения абсорбированных зарядов, а также мощности проводящего слоя.

Так как первичный электрический заряд и дипольный магнитный момент остаются практически неизменными, то такие эффекты как изменения полярности дипольного момента планеты или звезды, дрейф магнитного полюса, отклонение магнитного полюса от географического можно связать с процессами перераспределения абсорбированных электрических зарядов.

В качестве приложения описанной теории рассмотрим экзопланеты, относящиеся к типу горячих юпитеров [11]. Эти планеты являются газовыми гигантами, расположенными близко к родительской звезде. Из-за сильных приливных эффектов их собственное вращение синхронизуется с орбитальным и вследствие этого дифференциальное вращение в недрах планеты существенно ослабляется. В результате эффективность динамо в этих планетах резко падает. Поэтому можно считать, что магнитные поля этих астрофизических объектов обусловлены одним и тем же механизмом. Это позволяет предположить, что магнитный момент любого горячего юпитера µ = xµ GR , где коэффициент x имеет одинаковое значение для всех планет этого типа. Для типичного горячего юпитера HD 209458b наблюдательные оценки магнитного поля [12] приводят к величине µ = 0.1µ _J , где µ _J = 1.53 · 10 ³⁰ Гс · см ³ — магнитный момент Юпитера, что дает x = 0.0084.

• 1.75

• 2.00

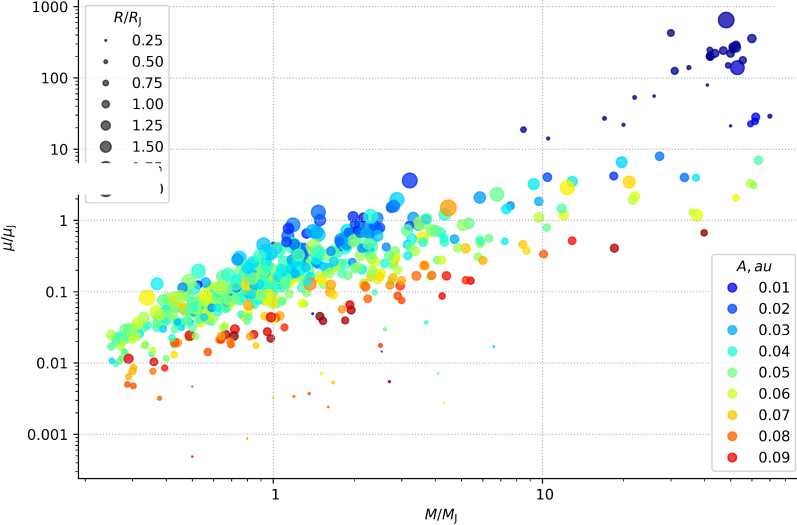
Рис. 1. Распределение магнитных моментов µ горячих юпитеров по их массам M . Размер кружков соответствует радиусу планеты R , а цвет — большой полуоси орбиты A .

На основе этих оценок можно найти магнитный момент любого горячего юпитера по известным значениям массы, радиуса и орбитального периода. На рис. 1 представлено распределение рассчитанных магнитных моментов µ горячих юпитеров (исходные данные взяты с сайта по массам M . Размер кружков соответствует радиусу планеты R. Видно, что большинство горячих юпитеров имеют магнитные моменты, лежащие в диапазоне значений 0.05 ≤ µ/µJ ≤ 0.5. Тем не менее, имеются планеты как с аномально низкими (µ < 0.01µJ), так и с достаточно сильными (µ = 5 – 10µJ) магнитными полями. В первую группу попадают компактные горячие юпитеры малого радиуса. Ко второй группе относятся массивные планеты, находящиеся очень близко к звезде. Такие планеты имеют короткие орбитальные периоды и, кроме того, из-за сильного нагрева излучением звезды их атмосферы нагреваются и вследствие этого расширяются. Данные соображения количественно обосновывают гипотезу Сазерленда-Эйнштейна.

В заключение необходимо отметить, что теоретическое обоснование гипотезы Сазерленда-Эйнштейна о причине возникновения магнитных полей астрофизических объектов, где магнитное поле у таких тел возникает, как суммарный эффект от наложения двух противоположных вкладов магнитных полей, генерируемых вращающимися с телом объемным и поверхностным зарядами, строилось в рамках геометрического подхода на основе синтеза пятимерных теорий Калуцы и Клейна. Данная теория позволила получить формулу для последующего эмпирического расчета магнитного момента определенного типа астрофизических объектов.

Важно сказать, что на основе этих оценок можно найти магнитный момент любого горячего юпитера по известным значениям массы, радиуса и орбитального периода (исходные данные взяты с сайта , что количественно обосновывает гипотезу Сазерленда Эйнштейна.

Изложенный выше материал данной статьи позволяет под новым углом зрения взглянуть на происхождение магнитных полей астрофизических объектов. А также внести теоретический и практический вклад для построения полной и обобщающей теории генерации магнитных полей астрофизических объектов и прогноза свойств данных полей.