Обоснование оптимальных параметров проектирования спецодежды для рабочих различных отраслей АПК

Износостойкость материалов в натурных условиях эксплуатации является сложным процессом, и его характер зависит от свойств, структуры, переплетения и отделки текстильных материалов при изготовлении спецодежды, а также от условий эксплуатации. В данный момент отсутствуют достоверные лабораторные методы оценки эксплуатационных свойств, и это проводит к необходимости проведения испытания тканей в процессе в натурных условиях. Разработанная математическая модель позволяет оптимизировать параметры проектирования спецодежды с учетом изменяющихся условий труда и характеристики используемых текстильных материалов.

Обьекты и методы исследования

При постановке экспериментов и обработке их результатов ставилась задача анализа и обоснования параметров проектирования специальной одежды рабочих различных отраслей АПК во всей области исследуемого факторного пространства. Также было необходимо определить оптималь- ные условия и исследовать окрестность в области факторного пространства для следующих физико-механических свойств, которые в дальнейшем были приняты за параметры оптимизации:

– разрывная нагрузка ткани по основе, НP o ;

– разрывная нагрузка ткани по утку, НP y ;

– истирание по плоскости, циклы.

Поиск многомерных зависимостей для разрывной нагрузки плотности ткани по основе, по утку и истиранию по плоскости осуществлялся в условиях ограниченного объема лабораторных данных и априорной неопределенности относительно вида функций регрессии для этих показателей.

Вначале были проведены однофакторные эксперименты, в которых исследовалось влияние температуры окружающей среды, продолжительности воздействия солнечных лучей, волокнистого состава материала и пылепрони-цаемости на разрывную нагрузку ткани по основе. Результаты этих однофакторных экспериментов, проведенных в трехкратной повторности, представлены в таблице 1.

Таблица 1 – Результаты однофакторных экспериментов на прочность ткани

Опыт	Фактор				Повторность			Среднее P o
	Т,°С	τ, час	φ, %	П, %	P o1	P o2	P o3
1	0	2	90	1,5	2020	2180	2220	2140
2	10	4	85	1,8	1780	1710	1730	1740
3	15	6	70	2,5	920	945	955	940
4	20	8	65	3,2	820	800	810	810
5	25	10	60	5,2	790	780	800	790
6	30	12	55	8,0	695	674	680	683
7	35	14	50	11,0	556	540	530	542
8	40	16	45	15,0	470	481	456	469

По данным таблицы построены точечные диаграммы и проведен подбор аппроксимирующих функций в виде полиномов второго и третьего порядков. Для пылепроницаемости более близкой оказалась логарифмическая функция.

На основе формулы (1) уравнение регрессии для управляемых в эксперименте факторов примет вид в качестве формулы (2):

д           k           k y = b0 + S bX + S bjxXj,   (1)

д y - значение критерия;

b_i - линейные коэффициенты;

действия факторов.

b _ij - коэффициенты двойного взаимо- pp   p

Y = f(xi,x2,...,Xp) = b0 + £btxtV^bjxx + £ bykxXjxk

i = 1              i , J = 1                   i , J , k = 1

• x i – независимые регулируемые переменные;

• p - управляемые факторы.

В формуле (2) члены первого порядка x i характеризуют главные эффекты, члены второго порядка x i x j (i ^ j) учитывают эффекты взаимодействия, дополнительные к линейным, эффекты совместного действия факторов x i и X j , а члены x i x_jx k (i ^ j ^ k) - эффекты совместного тройного взаимодействия факторов x i , x j и xkна исследуемые физикомеханические свойств ткани – разрывная нагрузка ткани по основе и по утку, истирание по плоскости. Расчет и анализ данных о тканях для проектирования специальной одежды механизаторов проводились на экспериментальных данных, которые позволили разработать и провести исследования на достоверных математических моделях. Нами учтены и обработаны все повторности лабораторных данных.

Это позволило более тщательно поста- вить эксперимент и максимально использовать всю информацию при построении адекватных моделей для параметров проектирования специальной одежды механизаторов.

В состав моделей прочности ткани в качестве независимых аргументов, которые менялись в ходе эксперимента, были включены 4 параметра:

• x 1 – температура окружающей среды во время уборки урожая (Т °С);

• x 2 – время воздействия солнечных лучей на материал (τ, ч);

• x 3 – волокнистый состав исследуемого материала (φ, %);

• x 4 – пылепроницаемость (П, %).

В соответствии с проводимыми экспериментами были приняты определенные условия планирования для исследуемых факторов и параметров проектирования специальной одежды механизаторов, а также выбраны диапазоны их варьирования, которые приведены в таблице 2.

Таблица 2 – Уровни варьирования факторов в экспериментах с ткани для специальной одежды механизаторов

Регулируемый фактор	Уровень варьирования			Шаг варьирования
	– 1	0	+ 1
x 1 – температура окружающей среды Т °С	0	20	40	20
x 2 – время воздействия солнечных лучей τ, ч	0	20	40	20
x 3 – волокнистый состав материала φ, %	40	65	90	25
x 4 – пылепроницаемость П, %	3	9	15	6

Для восстановления функций, характеризующих прочностные свойства тканей, был поставлен полный факторный эксперимент, план которого приведен в таблице 3.

Представленный план полного факторного эксперимента содержит множество всех точек в четырехмерном пространстве, координатами которых являются +1 (верхний уровень) или –1 (нижний уровень). Планы полного факторного эксперимента являются ортогональными планами первого порядка. С их помощью можно определить свободный член уравнения b0, коэффициенты bi, коэффициенты bij при парных взаимодействиях факторов, коэффициенты bijk при тройных взаи- модействиях факторов.

По данным таблицы 3 проводился корреляционный анализ с целью выявления влияния, влияют ли исследуемые факторы на физико-механические показатели ткани – разрывная нагрузка по основе и по утку, истирание по плоскости. Чтобы оценить степень этого влияния, когда исследуемые факторы имеют несколько градаций, составлены корреляционные таблицы и построены эмпирические линии регрессии. Посредством чего были установлены взаимосвязи и форма парных зависимостей между факторами x1,…,x4 и выбранными показателями (разрывная нагрузка по основе и по утку, истира- ние по плоскости).

В результате работы компьютерной программы «Correlations» статистического пакета SPSS 14.0 получена количественная мера взаимосвязи между исследуемыми факторами в виде симметричных относительно главной диагонали матриц парных коэффициентов корреляции [1,2].

Таблица 3 - Ортогональный план эксперимента для исследования прочностных показателей текстильных материалов

Опыт	Кодированные факторы				Функция отклика
	x 1	x 2	x 3	x 4	Y 1 = P o	Y 2 = P y	Y 3 = И
1	+	+	+	+	1715	940	15930
2	–	+	+	+	1720	945	15950
3	+	–	+	+	1700	930	15900
4	–	–	+	+	1730	950	15970
5	+	+	–	+	1670	900	15750
6	–	+	–	+	1685	910	15860
7	+	–	–	+	1690	920	15875
8	–	–	–	+	1665	890	15750
9	+	+	+	–	1740	960	16000
10	–	+	+	–	1750	975	16100
11	+	–	+	–	1755	980	16150
12	–	–	+	–	1758	985	16190
13	+	+	–	–	1752	920	15885
14	–	+	–	–	1655	910	15880
15	+	–	–	–	1600	790	15410
16	–	–	–	–	1586	780	15340

Таблица 4 – Коэффициенты парной корреляции в экспериментах с тканями для специальной одежды

Показатель	Выходная переменная			Входная переменная
	Y 1 = P o	Y 2 = P y	Y 3 = И	x 1 = T	x 2 = τ	x 3 = φ	X 4 = П
Y 1 – разрывная нагрузка плотности	1,000	0,942**	0,934**	0,089	0,247	0,688**	-0,026
ткани по основе, Н		p<0,001	p<0,001	p=0,743	p=0,356	p=0,003	P=0,925
Y 2 – разрывная нагрузка плотности	0,942**	1,000	0,991**	-0,005	0,257	0,704**	0,093
ткани по утку, Н	p<0,001		p<0,001	p<0,984	p=0,337	p=0,002	P=0,732
Y 3 – истирание по плотности, циклы	0,934**	0,991**	1,000	-0,039	0,216	0,685**	0,008
	p<0,001	p<0,001		p=0,885	p=0,421	p=0,003	P=0,975
x 1 – температура окружающей среды	0,089	-0,005	-0,039	1,000	0,000	0,000	0,000
(Т °С)	p=0,743	p<0,984	p=0,885		p=1,000	p=1,000	P=1,000
x 2 – время воздействия солнечных	0,247	0,257	0,216	0,000	1,000	0,000	0,000
лучей,ч.	p=0,356	p=0,337	p=0,421	p=1,000		p=1,000	P=1,000
X 3 – волокнистый состав (φ), %	0,688**	0,704**	0,685**	0,000	0,000	1,000	0,000
	p=0,003	p=0,002	p=0,003	p=1,000	p=1,000		P=1,000
x 4 – пылепроницаемость, (П), %	-0,026	0,093	0,008	0,000	0,000	0,000	1,000
	p=0,925	p=0,732	p=0,975	p=1,000	p=1,000	p=1,000

В таблице 4 приведены коэффициенты парной корреляции для общей (n = 16) совокупности экспериментальных данных, которые были получены в опытах с тканями для специальной одежды механизаторов по ортогональному плану.

Исследуя полученные коэффициенты корреляции таблицы 4, можно отметить, что многие пары переменных имеют тесную связь.

Отслеживается стабильное положитель- ное влияние x3 – волокнистого состава на все прочностные параметры ткани, подтвержденное значимыми коэффициентами парной корреляции.

Наблюдается очень тесная связь (с r свыше 0,9) между исследуемыми физикомеханическими показателями ткани. Регулируемые параметры x1, x2, x3, x4 имеют между собой нулевую корреляцию, то есть являются взаимно независимыми. В таблице 4 для каждого коэффициента корреляции между входными x1, x2, x3, x4 и выходными показателями - разрывная нагрузка по основе и по утку, истирание по плоскости, приводится соответствующий ему уровень значимости коэффициента корреляции.

В таблице 5 приводятся результаты расчета моделей регрессии для исследуемых показателей прочности ткани – разрывная нагрузка по основе и по утку, истирание по плоскости.

В верхней части таблицы 5 приведены результаты расчета полных моделей с линейными, парными и тройными взаимодействиями, которые в большей части дублируют эффект влияния на прочностные показатели ткани. В нижней части этой таблицы представлен окончательный вариант регрессионного моделирования показателей ткани, полученный после исключения статистически незначимых компонентов уравнения регрессии.

Анализируя данные таблицы 5, следует отметить высокую значимость влияния многих составляющих в полученных уравнениях регрессии на показатели - разрывная нагрузка по основе и по утку, истирание по плоскости. Наибольшее влияние на результирующий показатель оказывают те члены уравнения регрессии, у которых t-критерий Стьюдента

P o =1698,2+12,6875 x 2 +35,3125 x 3 +x 1 x 2 –10,5625 x 1 x 3 –14,9375 x 2 x 3 –12,0625 x 2 x 4 – – 15,9375 x 3 x 4 + 15,5625 x 2 x 3 x 4 ,

P y = 917,8 + 14,6875 x 2 + 40,3125 x 3 + 5,3125 x 4 – 5,3125 x 1 x 3 – 17,8125 x 2 x 3 – – 14,0625 x 2 x 4 – 22,1875 x 3 x 4 + 18,4375 x 2 x 3 x 4 ,

И = 15871,25 + 48,1250 x 2 + 152,5000 x 3 – 19,375 x 1 x 2 – 20,0 x 1 x 3 – 76,875 x 2 x 3 – – 48,75 x 2 x 4 – 88,125 x 3 x 4 + 18,125 x 1 x 2 x 3 + 80,0 x 2 x 3 x 4 ,

Значимость влияния исследуемых факторов и их комбинаций на физико-механические показатели ткани характеризуется величиной t-критерия Стьюдента [3].

Из значений t-критерия Стьюдента следует, что большинство членов в полученных уравнениях регрессии оказывают существенное влияние на исследуемые показатели ткани – разрывная нагрузка по основе и по утку, истирание по плоскости. Среди главных эффектов незначимым оказался фактор x 1 – температура окружающей среды во время уборки урожая (°С). Графически этот факт отражают диаграммы Парето, представленные на рисунке 1, на примере разрывной нагрузки по основе.

Проверка качества рассчитанных регрессионных моделей проверялась коэффи- по абсолютной величине превосходит 1,96. Такое же заключение можно сделать по рассчитанному значению статистического уровня значимости р. Компонент регрессии считается существенным, если для него величина уровня р ≤ 0,05.

При использовании метода пошаговой регрессии Backward в расчетах были приняты уровни значимости q=0,05 для критерия F-Entry (F-включения) и q=0,10 для критерия F-Removal (F-исключения). Вовлечение в модель переменных x i , их двойных x i x j и тройных x i x j x k взаимодействий производилось за соответствующее число шагов регрессионной процедуры. На каждом её этапе проводился перерасчет и анализ всех статистических характеристик моделей для обоснования параметров проектирования специальной одежды механизаторов [3].

Используя результаты регрессионного моделирования, полученные в пошаговой итерационной процедуре Backward с указанными выше параметрами уравнений(е, ж, з) для обоснования параметров проектирования специальной одежды механизаторов, полученные после исключения незначимых факторов, примут следующий вид уравнений (6-8):

циентами множественной корреляции, детерминации, критериями Фишера и Дарбина-Ватсона с оценкой их значимости при соответствующем числе степеней свободы, что представлено в таблице 5.

Коэффициент множественной кореляции между наблюдаемыми значениями, предсказанными по уравнению регрессии, характеризует множественную корреляцию между выходной величиной Y, с одной стороны, и всей совокупностью входных величин x 1 ,...,xр, с другой. Нулевое значение R указывает на то, что отклик Y не зависит (линейно) от набора переменных x 1 ,...,xр, а значение R=1 указывает на полную линейную зависимость. Коэффициент R есть мера полезности параметров b j (j= 1,…,p) в модели регрессии.

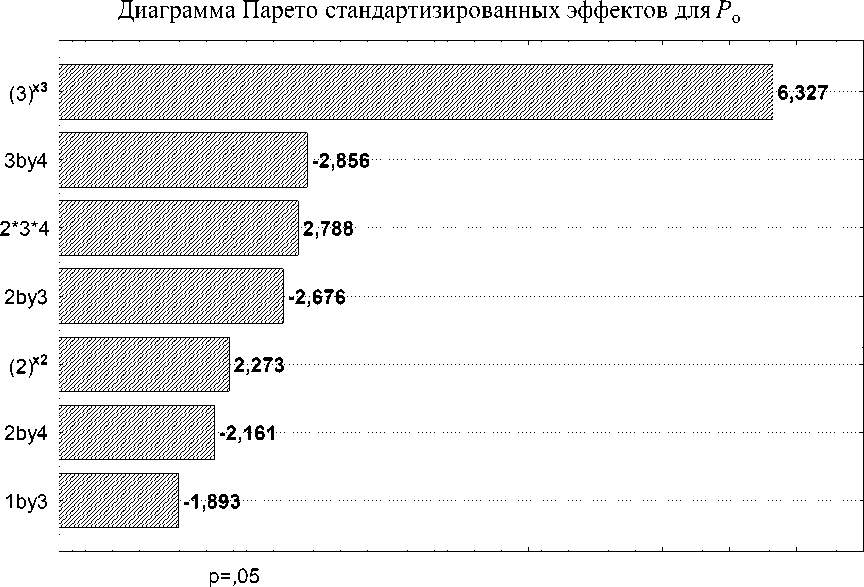
Оценка эффекта (абсолютное значение)

Рисунок 1 – Диаграмма Парето для оценки влияния факторов на разрывную нагрузку ткани по основе.

Таблица 5 – Проверка адекватности и достоверности моделей прочности тканей для спецодежды комбайнеров

Статистические критерии адекватности модели регрессии	Показатель прочности ткани
	Po (4.24)	Py (4.25)	И (4.26)
Множественная корреляция R ……............….	0,9515	0,9953	0,9955
Коэффициент детерминации R 2 …....................	0,9054	0,9907	0,9910
Критерий Фишера F……………......................	10,935	93,476	73,100
Число степеней свободы df: k 1 ; k 2 …................	7; 8	8;7	9; 6
Значимость F……………………......................	1,55Е-03	2,02E-06	1,93E-05
Критерий Дарбина-Ватсона d ….....................	3,1114	2,6013	2,8191

Коэффициент детерминации R 2 , равный квадрату скорректированного на число степенной свободы коэффициента множественной корреляции, служит для измерения совокупного влияния, оказываемого всеми исследуемыми факторами x 1 ,..., x р на результат – показатель прочности ткани [4].

Коэффициент детерминации R 2 указывает долю вариации отклика, выраженную регрессией показателей – разрывной нагрузки ткани по основе и по утку, а также истирание ткани по плоскостипо x 1 ,...,x р , и характеризует качество и достоверность аппроксимации. Чем больше R 2 , тем лучше модель аппроксимирует с выбранными показателями ткани.

Критерий Фишера F проверяет значимость всего уравнения регрессии. Расчетное значение критерия Фишера F сравнивается с табличным критическим значением при соответствующем уровне значимости q (q = 0,05 или q = 0,01) и числе степеней свободы df1 = p и df2 = n – p – 1 соответственно для числителя и знаменателя.

Наличие сериальной корреляции в регрессионных остатках ei ( e i = y i - € i , i = 1,...,n) показателей прочности ткани для специальной одежды механизаторов устанавливалось критерием Дарбина-Ватсона d.

Многомерные регрессионные модели, полученные после исключения незначимых компонентов, достаточно полно характеризуют влияние исследуемых факторов на физико-механические показатели ткани, так как имеют высокие коэффициенты множест- венной корреляции, которые лежат в пределах от 0,951 до 0,995. Эти уравнения хорошо описывают экспериментальные данные, так как сумма квадратов, обусловленная регрессией, составляет более 90% от полной суммы квадратов. Критерий Фишера меняется от 10,935 до 93,476 и имеет уровень статистической значимости менее 0,001. При сопоставлении расчетных и табличных значений критерия Дарбина-Ватсона, сериальная корреляция в остатках регрессионных моделей отсутствует на уровне q=0,05. Все это свидетельствует о достоверности и высокой адекватности полученных моделей.

Результаты и их обсуждение

Модели для оценки физико-механических свойств ткани, полученные для всей совокупности опытных данных методом пошаговой регрессии, хорошо аппроксимируют данные поставленных экспериментов. Модели имеют высокую 95%-ную достоверность и, согласно F-критерия Фишера, статистически значимы на уровне p<0,001.

Статистические критерии наряду с отсутствием сериальной корреляции в регрессионных остатках показали высокую информативность и достоверность полученных моделей. Эти модели позволили определить оптимальную область регулируемых факторов, вне которой улучшение прочностных показателей не принесет пропорционального эффекта, воздействующих на процесс проектирования специальной одежды механизаторов.

Выводы

Таким образом, по результатам статистической обработки и анализа экспериментальных данных построены достоверные регрессионные модели для прочностных показателей ткани в зависимости от исследуемых факторов. В модели регрессии включались статистически значимые и наиболее важные факторы и их комбинации, объясняющие формирование показателей ткани.