Обоснование параметров установки дополнительных почвообрабатывающих орудий в пахотных агрегатах с учетом движения почвенного пласта по поверхностям корпуса плуга
Автор: Чигарев Юрий Власович, Савиных Петр Алексеевич, Назаров Федор Игоревич, Крук Игорь Степанович, Романюк Вацлав
Журнал: Молочнохозяйственный вестник @vestnik-molochnoe
Рубрика: Технические науки
Статья в выпуске: 4 (32), 2018 года.
Бесплатный доступ
В статье получено уравнение движения пласта по отвалу в зависимости от скорости агрегата, характеризующего кривизну траектории угла, силы тяжести пласта, прилагаемой силы тяги и силы сопротивления, обусловленной переупаковкой частиц почвенного пласта при его подъеме по отвалу. Получены аналитические выражения для определения времени движения пласта по отвалу, определения координат падения пласта на поверхность поля и оценки времени падения. Полученные результаты могут быть использованы в области сельскохозяйственного машиностроения при проектировании оборотных плугов и дополнительных орудий, предназначенных для поверхностной обработки почвенных пластов к ним.
Плуг, орудие, обработка, почвенный пласт, частица, сила, скорость, движение, траектория, зависимость
Короткий адрес: https://sciup.org/149126689
IDR: 149126689 | УДК: 631.363
Текст научной статьи Обоснование параметров установки дополнительных почвообрабатывающих орудий в пахотных агрегатах с учетом движения почвенного пласта по поверхностям корпуса плуга
Экономическая и технологическая эффективность дополнительной поверхностной обработки почвенного пласта одновременно со вспашкой определяется конструкцией пахотного агрегата. Технологический процесс совмещения вспашки и поверхностной обработки почвенных пластов осуществляется следующим образом. Почвенный пласт подрезается и начинает подъем по лемеху, далее происходит скольжение по поверхности отвала, поворот и частичное крошение. Пласт почвы отбрасывается с поверхности отвала под углом к горизонтальной и вертикальным плоскостям и падает на поверхность поля на некотором расстоянии от корпуса плуга. Наименьшее расстояние установки дополнительных устройств определяется условием полного оседания частиц почвы, которым была передана энергия движения корпуса плуга до начала воздействия на почву рабочих органов дополнительных орудий (рис. 1) . То есть в момент соприкосновения рабочего органа дополнительного устройства почвенный пласт должен быть неподвижен.
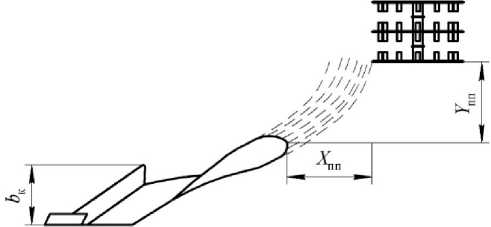
Рисунок 1. Схема установки дополнительных почвообрабатывающих устройств относительно корпуса плуга
Как показывает практика, нерациональная установка почвообрабатывающих устройств относительно корпуса плуга влияет на энергоемкость, материалоемкость и качество выполнения технологического процесса.
Результаты и их обсуждение
Дальность отбрасывания частиц почвенного пласта отвалом определяется скоростью движения агрегата, типом и параметрами отвала, размерами и состоянием пласта [1‒10]. Для изучения закономерностей оборачивания и отбрасывания почвенного пласта корпусом плуга применяются следующие допущения: пласт принимается за материальную точку, скорость агрегата со временем не меняется, поверхность отвала имеет постоянный радиус кривизны [10‒14]. Почвенный пласт подрезается лемехом корпуса и движется по поверхности отвала. Данное движе- ние рассматривается как относительное, подвижная система отсчета связана с отвалом. При подрезании слоя почвы начальная величина относительной скорости принимается равной величине скорости агрегата. Отметим, что отвал имеет довольно сложную конфигурацию, поэтому определять его поверхность как окружность, можно с большим приближением. В нашем случае кривизна отвала описывается не радиусом окружности, а уравнениями циклоиды, которую образуют точки окружности радиуса rц (рис. 2).
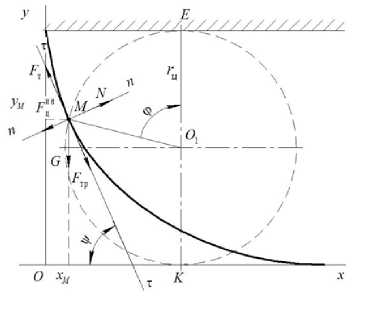
Рисунок 2. Кинематика движения почвенного пласта
Рассмотрим движение пласта массой m п на поверхности отвала. Свяжем с точкой подвижную систему координат ( τ, n ). Ось τ - τ касательная к циклоиде, n - n нормаль. Точка движется вдоль касательной к траектории движения, которая в каждый момент времени меняет направление. Запишем уравнение движения относительно оси τ - τ . На точку будут действовать сила тяжести G = mn9 ( у ускорение F = us свободного падения, м/с2), сила внутреннего трения частиц пласта почвы * тр
(μ коэффициент сопротивления (вязкости), Н∙с/м; S - скорость почвенного пласта, м/с), s=BM путь, пройденный точкой М за время t1, м), сила тяги ^r и центробежная сила инерции F^ =-mnan (^ нормальное ускорение), сила реакции поверхности отвала N . Здесь и далее точками над буквами обозначаем производную по времени t1. Сила сопротивления обусловлена внутренним трением движения частиц пласта почвы (крошение, перемешивание, переупаковка порового пространства) [10‒15].
Имеем:
mn—=-mngsuiip-F^ + FT
,
где ψ ‒ угол наклона касательной, проведенной к циклоиде в точке М, к горизонту, град.
Учитывая, что ^тр F , уравнение (1) можно записать в следующем виде mn^=-mn9™^-F^ + ^
где s=BM путь пройдённый точкой М за время t1.
Данное уравнение содержит три переменные s, t1, ψ. Предположим, что по- верхность отвала может быть описана уравнением «перевернутой» циклоиды, где rц ‒ радиус катящегося по горизонтальной линии (потолку) круга (см. рис. 2):
x = ^Ц(<Р + simp)’ у = гц(1 + cos
где φ ‒ угол между прямой, проведенной из центра круга О1, перпендикуляр- но потолку и отрезком, соединяющим точку М и центр круга О1.
Из уравнений (3) составим выражение для производной: dy=_ rusiiiffl = _ 2an®cos|
В тоже время дифференциал дуги циклоиды есть выражение:
ds = |l + (—)2dx .
Подставив равенство (4) в (5) д ифференц иал дуги циклоиды будет:
dS “ ]1+ tg 2dX .
Из первого уравнения (3) найдем:
dx =гц(1 — cos ср) dtp = 2rusin2 —
Тогда дифференциа л пути (6) будет равен:
ds =
11 +
ctg -^2rusm -^dcp
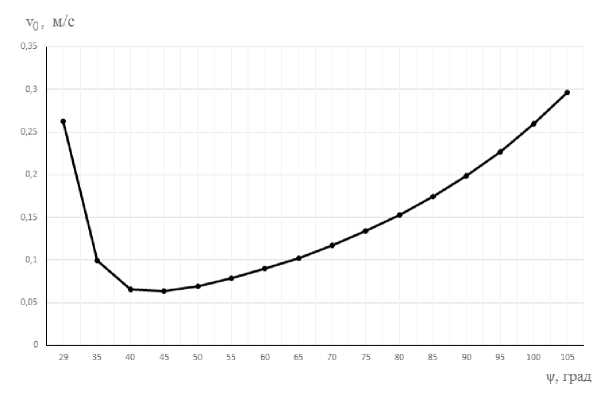
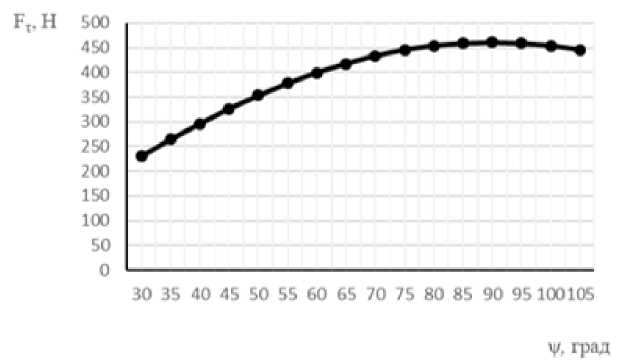
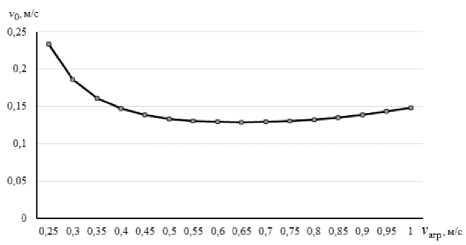
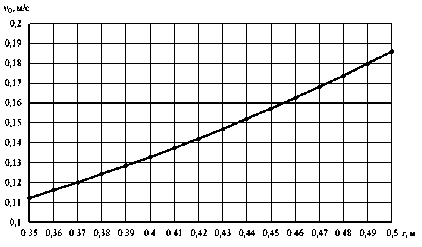
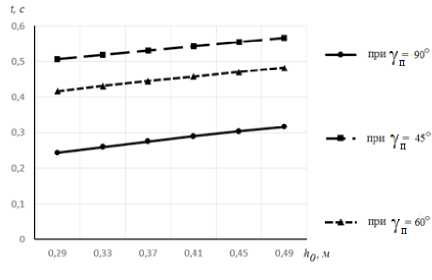
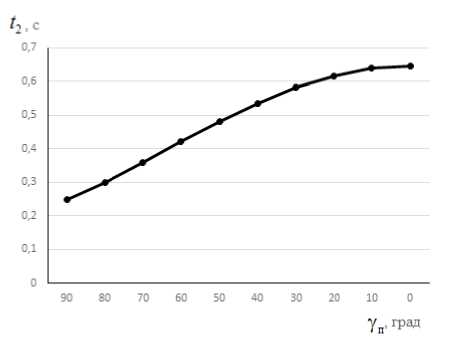
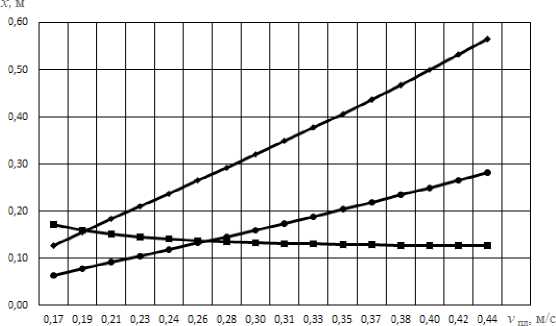
= 2гцзт—d После интегрирования (8) путь проходимого точкой почвы по плугу будет: Отсюда: s = о э ■ ^ J / 'PI 0 2гц sinyd 21^ = 4гц(1 - cosy) . cos— = 1 — 2 s ^\ . Согласно рисунку 2 можно записать: dx Учитывая равенство (4) путем простых преобразований получим: sinip = tgipcos i/j = . Сравнивая равенства (10) и (11) получим: s sin^ = 1-- 4гц. Уравнение движения (2) частицы почвы по поверхности плуга с учетом (12) запишется в виде: . ds где , . , Уравнение преобразуем к виду: mn9s mns = -mng + —— pis + FT. или - , 9s 9 FT s = — g 4- —---—s 4—- . Введем обозначение: A=^~ B-/- D=^x mn; 4гц; ™n . Тогда равенство (13) с учетом (14) приводит к уравнению: , где . Решение уравнения (15) запишем в виде суммы: S = Si + s2, где s1 ‒ общий интеграл уравнение, s2 ‒ частный интеграл уравнения. Решение однородного уравнения s + ,4s — Ss = 0 о Si = eAti ищем в виде 1 . Характеристическое уравнение I2 + 42 - S = 0 имеет корни: _-4± ^A2 4- 4B ^12 - ; Поэтому решение (16) имеет вид: , где t1 ‒ время движения почвы по корпусу плуга, с. Частное решение запишем в виде: . Так как s = 0,s = 0 то из уравнения (15) получим: Учитывая равенства (18) и (20) решение уравнения (15) будет: . В начальный момент времени t0 = 0, s0 = 0, (vп0 скорость почвенного пласта в начале лемеха), м/с. Продифференцируем равенство (21) по t1, получим: . Подставив начальные условия в равенства (21) и (22) получим систему уравнений: Данная система имеет решение, так как: . Решая систему (23) найдем: . , Следовательно: ’ Л 7л2 + 45 (24) _ ^2 _ EA i + vno ’ Д - 7л2 + 45 . (25) Подставим c1 и c2 в равенство (21) получим уравнение движения пласта почвы по поверхности плуга: s = ^2+1по ^^ _ gjl + Vno ^ti + £ 7л2+45 7л2+ 45 Взяв производную по времени (26) получим скорость движения пласта: = (^гЦпоЖ^^ _ (^VlnoUzg^ti 77^+45 7л2 + 45 . (27) Преобразуем равенства (26) и (27) к виду: s = , 7 \EA2eAltl + VnoC21^ - vnoeA2tl - E^e^] + 5 = / / [E(^2e21tl - Л^^1) + vno(e21tl - eA2t1)] + E Заметим, что: s =M^2^eAltl +vno21e+tl -vno22eAztl -Щ2е ;^[EA1A2(e+t1 -е+^ +^ , . Из физических соображений должно выполняться условие: . Из приведенных выше рассуждений следует, что сила тяги пласта почвы должна быть больше его силы тяжести, т.е. . Анализ равенств (28) и (29) показывает, что s и будет расти, если , т.е. сила тяги пласта почвы должна быть больше ее силы тяжести в каждой точке траектории движения по поверхности отвала. Для определения силы тяги вдоль плуга составим уравнения равновесия относительно касательной и нормальной осей. Рассмотрим систему сил, действующих на материальную точку пласта. Cилу тяги агрегата разложим на две составляющие вдоль осей FT и Fn: ; ; где mпч ‒ масса материальной точки пласта, кг. Откуда сила тяги: тр 4- тпчд sinip = fN + тпчд sinip. Определим N: , где F0 ‒ сила тяги плуга, Н. Подставив равенство (34) в (33), получим силу тяги: Ft =f (Fq sin ip 4- тпчд cosip) + mmg sinip = {Fq sinip 4- mn4g(f cos ip 4- sinip). При ψ=0, сила тяги действующая на пласт почвы будет равна тяге плуга в случае покоя: . Вход пласта на плуг происходит при 30°, а сход при 90°. ip = - При из равенства (34) имеем: . При сходе пласта с поверхности плуга f = 0 и следовательно: . В формулах (28) и (29) разложим (i = 1, 2) в ряд Тейлора, ограничиваясь линейными членами. Тогда равенство (28) можно записать в виде: s - j^Lr ^[^С1 + ^i£i) _ ^i(l + ^i)] + vno(l + ^^ - 1 - 4^1) ] = /,2 [^(^2 - ^1) + Vno] + Тл^+4В [vno(^l ^2)]- Откуда найдем время движения пласта почвы по отвалу корпуса плуга: , 11 [VnoGi -л2)]=з~ 1 №-->1) +»По]- 7л2 + 4В 7л2+4В т.е. _ s^Ia2 + 4g - E^-AJ - vno vno Pl “ ^2) . (40) Зная время движения пласта по отвалу, определяемое по формуле (40), по формуле (29) можно определить его скорость VD = S вдоль траектории s, в том числе и скорость на кромке отвала, которая в момент времени t1 будет равна . С помощью формул (14), (29), (34), (40) можно исследовать кинематику движения пласта, закономерность изменения его скорости движения по поверхности плуга в зависимости от изменения угла ψ. Как видно из рисунка 3, скорость точек пласта относительно корпуса плуга в начальный момент времени резко падает, что связно с началом деформации почвенного пласта на лемехе плуга (сгруживание). Далее почва попадает на отвал и начинает ускоряться. Рисунок 3. Зависимость скорости движения пласта от его положения на корпусе плуга (угла ψ) Согласно рисунку 4 сила тяги пласта на поверхности плуга по траектории циклоиды так же растет до 85°, после чего начинает падать. Рисунок 4. Зависимость силы тяги от угла наклона траектории При построении графиков учитывался максимально возможный путь материальной точки пласта. Построены зависимости изменения скорости движения пласта от скорости агрегата (рис. 5) и пути, пройденного по траектории (рис. 6). Рисунок 5. Зависимость скорости движения Рисунок 6. Зависимость скорости v0 от длины пласта на выходе с отвала от скорости движе- пути s ния плуга Полученные выше параметры движения частиц почвы были связаны с ее относительным движением относительно движущегося плуга. Далее частица пласта вылетает с верхней кромки отвала, двигается в пространстве относительно неподвижной системы координат (рис. 7). Начальная скорость полета частицы пласта будет равна ее конечной скорости на кромке отвала, которую можно получить из формулы (27) или (28) подставив в нее время движения частицы почвы по отвалу. Полет пласта почвы при отсутствии сил сопротивления воздуха можно описать уравнениями движения [15]: тпх = О, mny = О< mnz = — тд. (41) . Подставим равенство (46) в третье уравнение (45) получим уравнение траек- тории: z = ^O + y)2 2v^( cos Яд + cos £n)2 . ^syn(x + y) , , ’ -----------------------' "O' cosan + cos^n Определим время падения пласта почвы из третьего уравнения (45), принимая z = 0: О^^+уо^созУп. + Ао , , 2Vq cos yn ± 4v§cos2yn + S^Aq 2$ . Время падения будет соответствовать положительному значению выражения (48). Как видно из формулы (48), время падения частицы почвы на поле зависит от скорости на кромке отвала, высоты корпуса плуга и угла между осью Оz и вектором Y = — скорости на кромке отвала. При 2 имеем минимальное времени падения: . Изменение времени падения, определяемого по зависимостям (48) (при м/с) и (49), представлено на рисунке 8. Полагая, что поступательное движение плуга осуществляется вдоль оси у, определим координату (x; y) места падения пласта почвы на поверхность поля. Учитывая равенство (49), из первых двух уравнений (45) получим: . Отметим, что углы α, β, γ задаются конструктивными параметрами плуга (кромки отвала). Полученные значения координат будут показывать ближайшую к корпусу точку, поэтому к окончательному значению необходимо добавить высоту пласта (глубину обработки). а) б) Рисунок 8. Зависимости времени полета частицы t от высоты h0 (а) угла γп (б) На рисунке 9 показана зависимость дальности полета частицы от скорости корпуса плуга и траектории движения частицы, представлены графики, построенные на основании результатов расчета дальности падения частиц почвы, сошедших с кромки отвалов корпусов в зависимости от скорости движения плуга: а при принятой траектории движения почвы по отвалу в виде дуги окружности (поверхность отвала имеет постоянный радиус кривизны) [10], б при принятой траектории движения почвы по отвалу в виде дуги окружности с учетом экспериментального поправочного коэффициента [10]; в при принятой траектории движения почвы по отвалу в виде циклоиды на основании полученных в статье формул. Очевидно, что наиболее приближен к реальному поведению почвенного пласта график (в), так как у при повышении скорости пласт начинает лучше крошится и равномерно распределяется по борозде. -^ a) -~ б) * в) Рисунок 9. Зависимость дальности полета частицы от скорости движения корпуса плуга и принятой траектории Выводы В результате проведенных теоретических исследований получено уравнение движения пласта по отвалу в зависимости от скорости агрегата, характеризующего кривизну траектории угла, и силы тяжести пласта, силы тяги, силы сопротивления, обусловленной перекомпоновкой частиц почвенного пласта при его подъеме по отвалу. Получены аналитические выражения для определения времени движения пласта по отвалу, определения координат падения пласта на поверхность поля. Полученные результаты могут быть использованы в области сельскохозяйственного машиностроения при проектировании оборотных плугов и дополнительных орудий, предназначенных для поверхностной обработки почвенных пластов к ним.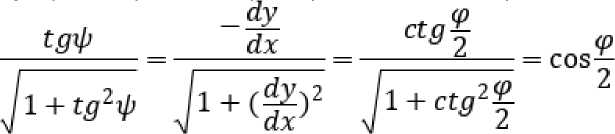
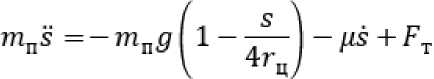
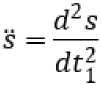
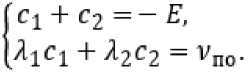
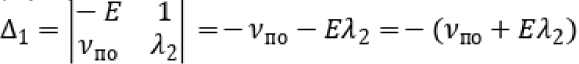
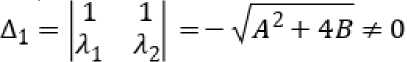
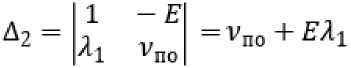
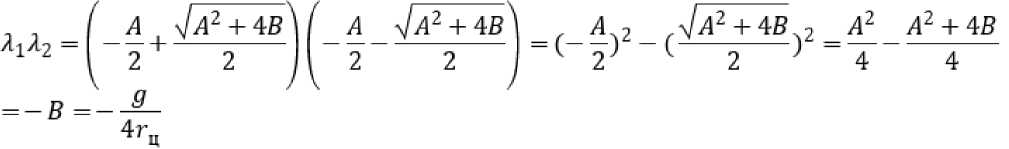
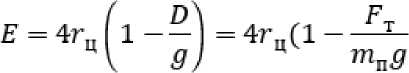
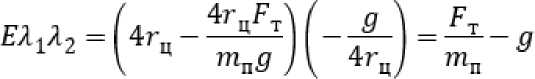
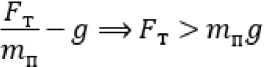
О У 1 / Г у
Рисунок 7. Траектория движения пласта почвы
После интегрирования имеем:
X = СЬ
* = c1t2 + c2,
У = ^
y = c3t2 + c4, ►
^z = -5t2 + c5,
^f2
Z =---+ Cctn +
2 j z о (42)
где t2 ‒ время полета частицы почвы, с.
При t2 = 0, z = h0, v = v0, (h0 высота от поверхности почвы до кромки отвала,
м).
%o=voc°san» *o = O'^
Уо^осо^п; Уо=°Л
±0=v0cosyn; z0 = hQ. (43)
Найдем ci (i = 1…6):
C1 = vo cosan/ c2 = 0, c3 =v0cos/?n, c4 = Oj c5 =v0 cosyn, c6 = Ло- J (44)
Подставим значения (44) в (42), получим уравнения движения: fx = v0t2 cosan, ly = v0t2 cos Дп.
1 z =-----M- vn cos yn, 4- nn-
2 и z * п и (45)
Из первых 2-х уравнений (45) получим:
,
откуда:
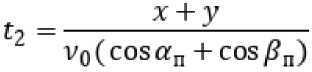
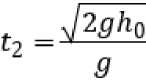
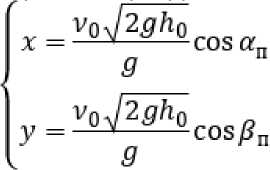
Список литературы Обоснование параметров установки дополнительных почвообрабатывающих орудий в пахотных агрегатах с учетом движения почвенного пласта по поверхностям корпуса плуга
- Сельскохозяйственные машины. Практикум: учебное пособие для студентов учреждений высшего образования по агрономическим специальностям/Э.В. Заяц ; ред. Э.В. Заяц. 2-е изд., доп. и испр. -Минск: ИВЦ Минфина, 2014. -432 с.
- Заяц, Э.В. Сельскохозяйственные машины: учебник для студентов учреждений высшего образования по агрономическим специальностям/Э.В. Заяц. -Минск: ИВЦ Минфина, 2016. -428 с.
- Капустин, В.П. Сельскохозяйственные машины: учебное пособие/В.П. Капустин. -М.: НИЦ ИНФРА-М, 2016. -280 с.
- Непарко, Т.А. Технологии и техническое обеспечение производства продукции растениеводства: учебное пособие для студентов учреждений высшего образования группы специальностей «Агроинженерия»/Т.А. Непарко, А.В. Новиков, И.Н. Шило; под общ. ред. Т.А. Непарко. -Минск: ИВЦ Минфина, 2015. -199 с.
- Щеголихина, О.В. Почвообразование, состав и особенности почв: практическое пособие для студентов специальности 1-75 01 01 «Лесное хозяйство»/О.В. Щеголихина, Н.В. Митин. -Гомель: ГГУ, 2017 -47 с.
- Лепешкин, Н.Д. Преимущества и недостатки вспашки в борозде и вне борозды/Н.Д. Лепешкин, Ф.И. Назаров, Д.В. Заяц//Белорусское сельское хозяйство. -2014. -№ 11. С. 92-94.
- К обоснованию динамических нагрузок, действующих на пахотный агрегат при навешивании на раму плуга катковых приставок/Ф.И. Назаров //Перспективи i тенденцiї розвитку конструкцiй та технiчного сервiсу сiльськогосподарських машин i знарядь: збiрник тез IV Всеукраїнської науково-практичної конференцiї, Житомир, 28-29, березня 2018 р. Житомирський агротехнiчний коледж; ред.: М.М. Тимошенко . -Житомир, 2018. -С. 263-266.
- Эффективность использования катковых приставок в пахотных агрегатах/С.Н. Герук //Перспективи i тенденцiї розвитку конструкцiй та технiчного сервiсу сiльськогосподарських машин i знарядь: збiрник тез III Всеукраїнської науково-практичної конференцiї, Житомир, 29-30, березня 2017 р. Житомирський агротехнiчний коледж; ред.: М.М. Тимошенко . -Житомир, 2017. -С. 220 223.
- Назаров, Ф.И. Совмещение операций основной и поверхностной обработки почвы/Ф.И. Назаров, И.С. Крук, Ю.В. Чигарев//Перспективи i тенденцiї розвитку конструкцiй та технiчного сервiсу сiльськогосподарських машин i знарядь: збiрник тез II Всеукраїнської науково-практичної конференцiї, Житомир, 78 квiтня 2016 р. Житомирський агротехнiчний коледж; ред.: М.М. Тимошенко . -Житомир, 2016. -С. 10-15.
- Проектирование катковых приставок для пахотных агрегатов. Рекомендации/И.С. Крук, Ф.И. Назаров, Ю.В. Чигарев, Г.Ф. Назарова, С.К. Карпович, Л.А. Маринич, Н.Г. Бакач, Н.Д. Лепешкин. -Минск: БГАТУ, 2017. -104 с.
- Определение параметров движения частиц почвенного пласта в процессе обработки оборотными плугами/И.С. Крук //Научно-технический прогресс в сельскохозяйственном производстве: материалы Междунар. науч.-прак. конф., посвящ. 70-летию со дня образования РУП «НПЦ НАН Беларуси по механизации сельского хозяйства», Минск, 1820 октября 2017 г. РУП «НПЦ НАН Беларуси по механизации сельского хозяйства»; редкол.: П.П. Казакевич (гл.ред) . -Минск, 2017. -С. 138 142.
- Обоснование параметров установки дополнительных орудий для поверхностной обработки почвенных пластов в пахотных агрегатах/И.С. Крук //Агропанорама. -2017. -№ 6. -С. 1016.
- Чигарев, Ю.В. Кинематические исследования движения почвенного пласта по поверхности корпуса плуга для обоснования параметров установки дополнительных почвообрабатывающих орудий в пахотных агрегатах/Ю.В. Чигарев, И.С. Крук, В. Романюк, Ф.И. Назаров//Проблемы интенсификации животноводства с учетом охраны окружающей среды и производства альтернативных источников энергии, в том числе биогаза: сб. ст. Институт технологических и естественных наук в Фалентах, отделения в Варшаве; редкол.: В. Романюк. Фаленты; Варшава, 2017. -С. 38-46.
- Гордеенко, О.В. Согласование технологических параметров дополнительных орудий при основной обработке почвы машинно-тракторными агрегатами с оборотными плугами/О.В. Гордеенко, И.С. Крук, Назаров Ф.И.//Передовые технологии и техническое обеспечение сельскохозяйственного производства: материалы Междунар. науч.-практ. конф., Минск, 30-31 марта 2017 г. Минск: БГАТУ, 2017. С. 365-369.
- Чигарев, А.В. Теоретическая механика: решение задач: учебное пособие для студентов учреждений высшего образования по техническим специальностям/А.В. Чигарев, Ю.В. Чигарев, И.С. Крук. -Минск: ИВЦ Минфина, 2016. -477 с.


