Обоснование выбора производительности вычислительных систем при неизвестных параметрах распределений рабочей нагрузки

Основным свойством, характеризующим объем работы, выполняемый вычислительной системой (далее – ВС) за определенный промежуток времени, является ее производительность [1; 9]. Требования к ней должны определяться в зависимости от планируемой рабочей нагрузки ВС и от требований к качеству ее обработки. Качество обработки в специализированных ВС часто характеризуется вероятностью отсутствия потерь заданий из-за превышения времени их обработки [3; 6]. Поскольку допустимое время пребывания заданий на обслуживании определяется динамикой развития внешних процессов, то требования к производительности ВС можно определить исходя из параметров входного потока и алгоритмов обработки информации. Однако на начальных этапах проектирования и модернизации ВС возникают трудности получения достоверных исходных данных.

В статье рассматриваются вопросы обоснования производительности вычислительных систем в условиях значительной неопределенности исходных данных, когда вероятностные законы для множества возможных значений параметров неизвестны. В этом случае задача обоснования характеристик требуемой производительности ВС, обеспечивающей устойчивость ее функционирования, сводится к задачам «игры с природой», для

Обоснование выбора производительности вычислительных систем при неизвестных ...

Гончаренко Владимир Анатольевич кандидат технических наук, доцент, преподаватель кафедры информационновычислительных систем и сетей. Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: устойчивость функционирования вычислительных систем, теория очередей, теория случайных процессов, адаптивное управление нагрузкой в информационно-вычислительных сетях. Автор более 90 опубликованных научных работ.

решения которых необходимы методы теории статистических решений (принятия решений в условиях неопределенности) [10].

Энтропийные подходы к учету неопределенности параметров

Неопределенность – это неполнота или недостоверность информации об условиях реализации решения, наличие факторов случайности или противодействия. Неопределенность различных явлений и процессов реального мира обуславливает необходимость разработки математических моделей, позволяющих учитывать этот объективно существующий фактор при принятии решений в любой практической области.

Меры неопределенности могут быть использованы для сравнения различных распределений. Мера неопределенности должна быть функционалом и не зависеть от конкретных значений случайной величины, непрерывной относительно аргументов, равной нулю при отсутствии всякой неопределенности, аддитивной , а также иметь максимум , отражающий наибольшую неопределенность.

В качестве меры неопределенности распределения вероятностей дискретной случайной величины обычно используется энтропия Шеннона

n

H = - ^ P k ln P k .

k = 1

Энтропия Шеннона является мерой неопределенности конечной схемы (случайного объекта с конечным множеством возможных состояний ).

Непрерывные случайные объекты (случайные объекты с континуумом возможных состояний ) не допускают введения конечной меры абсолютной неопределенности. Неопределенность реализации одного из бесконечного множества состояний может быть сколь угодно велика. Поэтому неопределенность выбора величины x из континуума значений X с плотностью распределения f ( x ) можно количественно определить относительно другой случайной величины с некоторым стандартным распределением. В качестве стандарта неопределенности для сравнения обычно берется неопределенность равномерно распределенной в единичном интервале случайной величины.

В качестве меры относительной неопределенности распределения вероятностей непрерывной случайной величины используется дифференциальная энтропия

∞

H _ε = - ∫ f ( x )ln f ( x ) dx .

Теория неопределенности предполагает, что последствия каждой альтернативы зависят от некой выборки всех возможных последствий, но лицо, принимающее решение (далее – ЛПР), не знает вероятности появления определенных последствий. Ему известен лишь набор возможных вариантов состояний внешней среды. В условиях неопределенности вероятностное распределение, соответствующее состояниям, либо неизвестно, либо не может быть определено [10]. Конструктивной идеей, позволяющей преодолеть объективно существующие трудности определения вероятностей в условиях неопределенности, является использование принципа максимума энтропии [11].

«Игра с природой» моделирует ситуацию, в которой одна сторона – «статистик» – человек или группа лиц с осознанной целью, вторая сторона – «природа» – комплекс внешних условий, при которых «статистику» приходится принимать решение. Для выбора оптимальной стратегии поведения в «игре с природой» используется ряд критериев. Каждый критерий наилучшим образом соответствует своей ситуации принятия решения и особенностям ЛПР.

Основные подходы к обоснованию производительности вычислительных систем в условиях неопределенности

Распространены три основных класса показателей производительности: продуктивность , реактивность и использование [9]. Показатели продуктивности используют при обосновании вычислительной мощности проектируемых ВС, удовлетворяющей определенному уровню рабочей нагрузки. При этом в качестве исходных данных обычно выступают объем вычислений и время выполнения этих вычислений [1]. В [6] на основе данных о рабочей нагрузке, а также в зависимости от ограничений, накладываемых на время ожидания обслуживания, определяется минимально необходимая производительность различных систем обработки информации. В [8] использован подобный подход для определения производительности ВС, обслуживающей рабочую нагрузку от нескольких объектов, состоящую из групп задач, сдвинутых друг относительно друга на некоторое время. При этом исходные данные могут быть заданы в форме начальных моментов распределений объема и времени вычислений. В [4; 7] решаются обратные задачи обоснования требуемой производительности вычислительных систем в терминах реактивности.

Сформулируем задачу следующим образом. Пусть параметры планируемой рабочей нагрузки ВС – интенсивность λ и трудоемкость обработки сообщений θ – заданы в виде множеств или диапазонов возможных значений [2; 5]. При этом предполагается, что об-

Обоснование выбора производительности вычислительных систем при неизвестных ...

работка сообщений должна производиться в реальном масштабе времени, т. е. до появления следующего требования. Производительность L ЭВМ определяется трудоемкостью θ и интенсивностью р обслуживания сообщений: L = р9 . Вероятность достижения цели функционирования определяется вероятностью отсутствия потерь сообщений из-за превышения времени пребывания на обработке Q . Если при реальной рабочей нагрузке Q примет значение больше 0,99, то цель функционирования достигается полностью; если же Q меньше 0,95, то информационно-вычислительный комплекс (ИВК) непригоден для выполнения поставленной задачи. Необходимо произвести выбор ВС с производительностью, обеспечивающей требуемое качество выполнения заданий и минимально возможные при этом материальные затраты.

Соотношение материальных затрат C на ВС с ее производительностью долгие годы определяли по закону Гроша: C = kL 0,5 , то есть получение добавочной экономии есть только квадратный корень от увеличения скорости. Другая трактовка закона гласит, что чем более дорог компьютер, тем отношение производительность/цена для него линейно лучше: L = kC ².

С достижением порога роста производительности и с развитием кластерных технологий каждый мегафлоп стал даваться труднее, и закон Гроша сначала трансформировался в линейный, а затем в степенной. Так, 100-машинный кластер нельзя сделать даже в два раза более мощным, чем 50-машинный, из-за ограничений закона Амдала. Аппроксимация закона Гроша для процессоров марки AMD Ryzen дала степенной коэффициент в диапазоне 1,02…1,4.

Рассмотрим конкретный набор исходных данных для отдельной ЭВМ. Интенсивность λ принимает одно из двух значений – λ1 или λ2 сообщения в секунду; трудоемкость θ также имеет два возможных значения – θ1 и θ2тысяч операций на обработку одного сообщения. Возможных состояний (стратегий) «природы» согласно исходным данным четыре: П1 = {λ1, θ1}, П2 = {λ2, θ1}, П1 = {λ1, θ2}, П1 = {λ2, θ2}. Пусть интервалы смежности и трудоемкость рабочей нагрузки распределены экспоненциально. Тогда для показателя эффективности результатов функционирования ЭВМ получим следующее выражение:

Р йц = P ( t <  t ^д ) = 1 - e ^{- (} ^ - ^{2 ) ?} .

Поскольку t = 1Д, а р = L /6, то для требуемой производительности L тр L >  L _mp = 2^ (1 + ln(1/(1 - Р _йц ))) .

Для четырех стратегий «природы» при Р _дц= 0,99, λ₁= 1 сообщ/с, λ₂= 2 сообщ/с, θ₁= 50 тыс. оп/с, θ₂ = 200 тыс. оп/с определим требуемые производительности:

П₁: L _тр = 280 258,5 оп/с; П₂: L _тр = 560 517,0 оп/с;

П₃: L _т^р_р = 1 121 034,0 оп/с; П₄: L ^р_тр = 2 242 068,0 оп/с.

Пусть имеются различные альтернативные ВС с производительностями:

A ₁: L = 1,5 млн оп/с; A ₂: L = 1,6 млн оп/с; A ₃: L = 1,7 млн оп/с;

A ₄: L = 1,8 млн оп/с; A ₅: L = 2,0 млн оп/с; A ₆: L = 2,2 млн оп/с;

A ₇: L = 2,5 млн оп/с; A ₈: L = 3,0 млн оп/с.

Введем в рассмотрение функцию полезности F _п. Будем считать, что максимальная полезность достигается, когда выбранное значение производительности ЭВМ совпало с требуемой, поскольку при этом цель функционирования достигается полностью, а материальные издержки минимальны. Представим функцию полезности F _п в виде матрицы, каждый член которой представляет собой произведение двух множителей:

f1 ij = f3 ij ■ fip ij , где i – номер выбираемой альтернативы; j – номер стратегии «природы».

Первый множитель f _{в ij} отражает выигрыш в материальных издержках при выборе ЭВМ и может быть представлен в следующем виде (Рисунок 1):

f =C :/C=(L /D ^0,5 f в ij       тр ij ' V тр ij

Второй множитель f _{пр ij} имеет смысл полезности принятого решения о производительности , при котором достигается соответствующее значение показателя качества Р _дц, но без учета материальных издержек.

При Р _дц > 0,99 f _{пр ij} принимает единичное значение, при Р _дц ≤ 0,95 – нулевое значение, а на интервале [0,95;0,99] – равномерно распределена (Рисунок 2):

f ip j = P^; 0,95 < р _дц < 0,99.

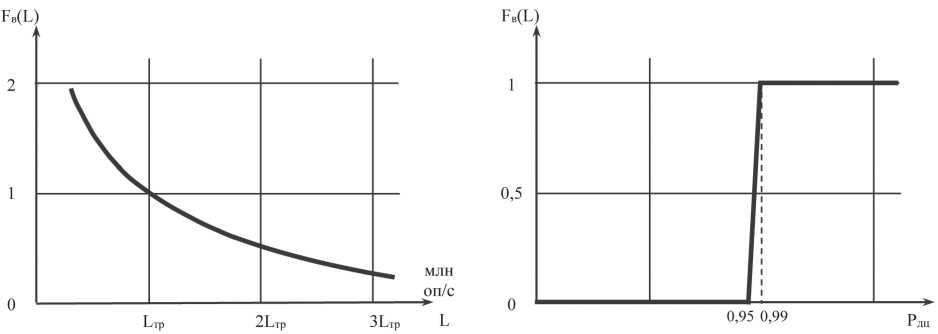
Рисунок 2. Зависимость функции полезности принятого решения F от вероятности достижения цели

Рисунок 1. Зависимость функции выигрыша F _в( L ) от производительности L при выборе ЭВМ

Рассчитанные значения функции полезности для различных вариантов производительности A _i и стратегий «природы» П_j приведены в Таблице 1.

Таблица 1

Значения функции полезности

	П 1	П 2	П 3	П 4
A 1	0,43225	0,61129	0,86450	0,00000
A 2	0,41852	0,59188	0,83705	0,00651
A 3	0,40603	0,57421	0,81205	0,32230
A 4	0,39458	0,55803	0,78918	0,55252
A 5	0,37434	0,52940	0,74868	0,83868
A 6	0,35692	0,50476	0,71383	0,98153
A 7	0,33481	0,47351	0,66963	0,94701
A 8	0,30565	0,43225	0,61129	0,86450

Обоснование выбора производительности вычислительных систем при неизвестных ...

Существуют различные критерии, согласно которым выбирается наиболее приемлемый вариант из имеющихся альтернатив. Рассмотрим несколько наиболее известных из них.

Критерий Вальда (наилучшего гарантированного результата, минимаксный), согласно которому оптимальным является выбор, гарантирующий полезность f _ij в любом случае не меньшую, чем для наихудшего альтернативного варианта при конкретной реализации параметров рабочей нагрузки:

fjj = ^maxmm(_ , ) .

Критерий Сэвиджа (минимума максимального риска). Под риском понимается разность между максимально возможной полезностью при конкретной реализации параметров и полезностью, обеспечиваемой при выборе конкретного варианта A _i:

r ij = max⁽ f_n jj ) - f_n jj .

Тогда критерий принимает вид

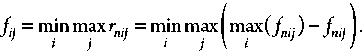
Как и критерий Вальда, критерий Сэвиджа – это критерий крайнего пессимизма, только пессимизм проявляется в том, что минимизируется максимальная потеря выигрыша по сравнению с достижимым в данных условиях.

Критерий максимального оптимизма ( максимакса ) основан на принципе, согласно которому выбирается вариант, обеспечивающий наибольший эффект в самой благоприятной ситуации. Данный критерий хорошо работает, когда потери для ЛПР в рассматриваемой ситуации малозначимы, или есть возможность повлиять на противоположную сторону, поэтому в «играх с природой», как правило, не используется:

f jj = ^{тахтах(} f „j ) .

ij

Критерий Гурвица ( пессимизма-оптимизма ). Является взвешенной комбинацией критерия Вальда и критерия максимального оптимизма:

f jj = maxi ^{к m}iⁿ⁽ f_n jj ) + (1 - к ) ^max( f_n jj )) ij                                       j

Критерий Байеса – Лапласа более оптимистичен, чем минимаксный критерий, однако предполагает большую информированность и достаточно длительную реализацию, p _j – вероятность состояния системы:

n fjj = max ^ Pjfn.j .

j = 1

Критерий Ходжа – Лемана характеризуется тем, что с помощью параметра выражает степень доверия к используемому распределению вероятностей. При v = 1 переходит в критерий Байеса – Лапласа, при v = 0 – в минимаксный критерий.

Критерий Гермейера обладает определенной эластичностью и определяется наименьшим произведением имеющегося результата на вероятность соответствующего состояния:

f jj = maxmin( P jf^j ) .

Составим на основе матрицы выигрышей матрицу рисков (Таблица 2).

Таблица 2

Матрица рисков

	П 1	П 2	П 3	П 4
A 1	0,00000	0,00000	0,00000	0,98153
A 2	0,01373	0,01941	0,02745	0,97502
A 3	0,02622	0,03708	0,05245	0,65923
A 4	0,03767	0,05326	0,07532	0,42901
м 5	0,05791	0,08189	0,11582	0,14285
A 6	0,07533	0,10653	0,15067	0,00000
A 7	0,09744	0,13778	0,19487	0,02452
A 8	0,12660	0,17904	0,25321	0,11703

Теперь можно принимать решения о выборе варианта ЭВМ в соответствии с одним из критериев. Проведем расчет по трем наиболее популярным критериям. Данные для выбора приведены в Таблице 3.

Таблица 3

Результаты расчета критериев выбора

	Критерий Вальда	Критерий Сэвиджа	Критерий Гурвица
	min( f ij )	max( r ij )	max( f ij )	κ = 0,8	κ = 0,9
A 1	0,00000	0,98153	0,86450	0,17290	0,08645
A 2	0,00651	0,97502	0,83705	0,17262	0,08956
A 3	0,32230	0,65923	0,81205	0,42025	0,37128
A 4	0,39458	0,42901	0,78918	0,47350	0,43404
A 5	0,37434	0,14285	0,83868	0,46721	0,42077
A 6	0,35692	0,15067	0,98153	0,48184	0,41938
A 7	0,33481	0,19487	0,94701	0,45725	0,39603
A 8	0,30565	0,25321	0,86450	0,41742	0,36154

В соответствии с критерием Вальда наиболее приемлемым является 4-й вариант. Согласно критерию Сэвиджа наиболее приемлемым является 5-й вариант. В соответствии с критерием Гурвица многое зависит от выбора коэффициента κ. При достаточно большом κ этот критерий близок к критерию Вальда (при κ = 0,9 – выбор 4-го варианта); при уменьшении κ начинает преобладать так называемый критерий максимального оптимизма (при κ = 0,8 – выбор 6-го варианта).

Таким образом, из имеющихся вариантов производительности наиболее приемлемыми являются А ₄, А ₅ и А ₆ . При ограничении материальных средств вполне приемлем вариант А ₄. Если же большее значение имеет обеспечение требуемого качества обслуживания заданий в сравнении с затратами, необходимо выбирать вариант А ₆. То есть могут быть сформулированы требования по производительности ко всем ЭВМ ИВК и произведен их выбор. Данный тип неопределенности относится к устранимым, поскольку по мере накопления информации уточняются параметры и характер рабочей нагрузки.

Обоснование выбора производительности вычислительных систем при неизвестных ...

На рассмотренном выше примере был использован подход к обоснованию производительности ЭВМ ИВК с применением показателей продуктивности. Аналогично может быть произведено обоснование выбора ЭВМ на основе показателей реактивности. Очевидно, что оба подхода взаимно дополняют друг друга при рассмотрении различных исходных данных и ситуаций выбора.

Выводы

Обоснование требований к характеристикам проектируемых информационновычислительных систем реального времени в условиях неопределенности параметров (в том числе действия возмущающих факторов) приводит к существенно более жестким оценкам данных характеристик. При обосновании производительности ВС возможны ситуации, когда мера неопределенности исходных данных неизвестна. В этом случае необходимо использовать методы теории полезности и принятия решений в условиях неопределенности и ввести в рассмотрение функцию риска (функцию затрат).