Образование конвективных валов на фоне продольного сквозного потока в активной неоднородной пористой среде со слабой закупоркой

Перенос примеси различных компонентов присутствует во многих задачах как фундаментального, так и прикладного плана. Количество примеси определяется её концентрацией в несущей жидкости. В относительно больших объёмах концентрация примеси зачастую распределяется неравномерно, что приводит к возникновению неоднородностей плотности и, в случае неустойчивой стратификации в поле силы тяжести, является причиной естественных конвективных течений. Эти течения могут генерироваться в неподвижных объёмах жидкости (или газа), а также на фоне основных вынужденных течений [1, 2] . В интенсивных потоках жидкости естественная конвекция, которая может быть вызвана не только неоднородностью концентрации, но и температуры, подавляется [3 –5] , поэтому её учёт целесообразен при относительно малых скоростях основного вынужденного течения. Обычно основной поток заключён в какой-нибудь канал, стенки которого создают сопротивление движению жидкости. Это сопротивление многократно возрастает, если жидкости дополнительно приходится просачиваться через пористый материал. Пористые среды значительно замедляют движение жидкости и тем самым создают условия для возникновения естественной конвекции (тепловой или концентрационной). В пористых средах можно создать большие неоднородности концентрации примеси или температуры, так как скорость фильтрации в них настольно мала, что не в состоянии размыть встречающиеся неоднородности.

Обычно задачи с прокачкой растворов сквозь пористую среду рассматриваются в связи с необходимостью очистки от примеси или для насыщения примесью основной жидкости или пористого материала. Очистка или насыщение возможно, если примесь ведёт себя некоторым образом согласованно с пористой средой, то есть является активной [6, 7]. При подходе в рамках сплошной среды такое взаимодействие усредняется, и учитываются кинетические уравнения с использованием сорбционных коэффициентов. При этом для описания транспорта примеси применима так называемая модель Mobile-Immobile Media (MIM-модель), где примесь делится на мобильную, движущуюся вместе с потоком несущей жидкости, и немобильную, оседающую на скелет пористой среды [8, 9]. В литературе представлен ряд задач [5, 10–12], в которых изучалось влияние коэффициентов адсорбции и десорбции на развитие естественной конвекции в пористой среде. В одних публикациях влияние сорбционных процессов на структуру этой среды игнорировалось [5, 10], а в других учитывалось и называлось эффектом закупорки [11, 12]. Показано, что уменьшение проницаемости пористой матрицы за счёт закупорки повышает порог возбуждения конвекции. Идентификация параметров транспорта примеси при её прокачке через пористую среду, таких как коэффициенты адсорбции и десорбции, концентрация насыщения (или максимальная концентрация) немобильной фазы, которые содержит нелинейная MIM-модель, производилась в [13, 14]. Результаты расчёта интегральных характеристик сквозного потока сопоставлялись с данными эксперимента. В пористых средах существенно усложнить задачу возникновения естественной конвекции на фоне основного вынужденного потока жидкости может неоднородность их фильтрационных параметров (пористости или проницаемости). Например, в относительно простой двухслойной системе горизонтальных пористых подслоёв [15], имеющих различные проницаемости, естественная конвекция принимает бимодальный характер, то есть в системе, в зависимости от её свойств, могут возникать конвективные подъёмно-опускные течения в пределах только одного из подслоёв (локальная конвекция) или в пределах всей системы (крупномасштабная конвекция). Впервые бимодальные нейтральные кривые устойчивости механического равновесия жидкости в слоистых системах, содержащих частично заполненную однородную неактивную пористую среду, опубликованы для систем в условиях подогрева снизу: в [16] для двухслойной и в [17] для трёхслойной. Подобные два вида конвекции наблюдались также при течении трёхкомпонентной смеси в двухслойной пористой среде [18] и однокомпонентной жидкости в среде с тремя пористыми подслоями [19]. Можно привести также ряд работ по анализу возникновения тепловой конвекции на фоне продольного [20, 21] и поперечного [22, 23] вынужденных течений в слоях, которые заполнены пористой матрицей частично. В данной работе рассматривается двухслойная пористая система, через которую прокачивается бинарная жидкость вдоль границы раздела горизонтальных подслоёв. Естественная конвекция в системе провоцируется перепадом концентрации тяжёлой примеси между внешними границами в изотермических условиях и в поле силы тяжести. Основной целью работы является исследование влияния сорбционных процессов (в том числе и эффекта закупорки) на устойчивость и структуру естественных конвективных течений с разной длиной волны, возникающих на фоне основного продольного сквозного течения. В статье продолжаются исследования, представленные авторами в [15], где внимание уделялось возбуждению стационарной конвекции после потери устойчивости механического равновесия жидкости, и подразумевало определение критических параметров колебательной конвективной неустойчивости вынужденного сквозного течения.

2. Постановка проблемы и методика решения

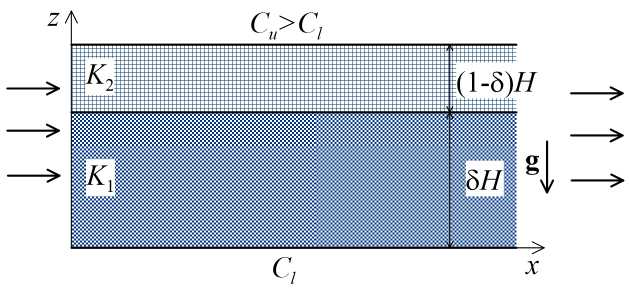
Рис. 1. Геометрия двухслойной пористой среды в поле силы тяжести при наличии продольного сквозного потока)

Рассмотрим неоднородную пористую среду, находящуюся в поле силы тяжести и состоящую из двух горизонтальных подслоёв, насыщенных бинарной смесью (Рис. 1). Проницаемость нижнего подслоя толщиной 6H равна K1, а верхнего подслоя толщиной (1 — 5) H, соответственно, K2. Пористая среда сверху и снизу заключена в непроницаемые границы. При наличии постоянного горизонтального градиента давления Vx P = —B (где B — положительная константа) в среде возникает плоскопараллельное продольное сквозное течение (течение Пуазейля). Бинарную смесь, насыщающую подслои, образуют лёгкая несущая жидкость и активная тяжёлая примесь (например, частицы наноразмера, тяжёлые металлы, бактерии и другое), которая может взаимодействовать с твёрдым скелетом пористой среды. Частицы смеси способны прилипать к пористой матрице и оставаться неподвижными в течение некоторого времени, а затем вернуться обратно в несущую жидкость. Их концентрация в несущей жидкости вблизи верхней границы составляет Cu = C0, а вблизи нижней границы—Cl = 0. Смесь неустойчиво стратифицирована по плотности в гравитационном поле, что при определённых условиях может привести к возникновению концентрационной конвекции на фоне основного течения Пуазейля. В работе для описания транспорта смеси в двухслойной пористой среде используется модель сплошной среды. Осаждение частиц учитывается в рамках нелинейной MIM-модели [8, 9], в которой подразумевается деление примеси на мобильную и немобильную фазы. Мобильная фаза движется вместе с несущей жидкостью. Концентрация мобильной фазы C определяется как отношению объёма мобильных «частиц» в несущей жидкости к полному объёму порового пространства, которое заполняется бинарной жидкостью. Немобильные частицы захватываются скелетом среды и имеют концентрацию Q, которая равняется отношению объёма осевших частиц к полному объёму пористой среды. Текущая пористость уменьшается с ростом концентрации немобильных частиц Q: ф = (ф0 — Q), ϕ0 — исходная пористость незагрязнённой среды. Проницаемость зависит от пористости и оценивается по формуле Кармана-Козени [2, 24]: K(ф) = Dpф3(1 — ф)-2/180, где Dp — средний размер неоднородности скелета среды. Для исследования конвективного движения смеси запишем уравнение Дарси, уравнение неразрывности, закон сохранения массы для мобильных и немобильных частиц в объёме среды и кинетическое уравнение распределения примеси между мобильной и немобильной фазами в каждом i-м пористом подслое (i = 1,2) [14, 15]:

—}u Ui =—VPi—Pf вс g(C—Ci)Y,(1)

K (фФ divUi = 0,

∂

- (фгСг +Qi) + (Ui V)C = div(Dфг VC),(3)

∂t

∂Q

~t^~ = a[Kd (Q0 — Qi)Ci — Qi], с граничными условиями:

z = 0:  Ci = Ci, Uiz = 0, z = 5H: Uiz = U2z, Pi = P2, Ci = C2, Dф1VzCi = Dф2VzC2,(6)

z = H: C2 = Cu, U2z = 0, где U — вектор скорости фильтрации, P — давление без учёта гидростатической добавки, D — коэффициент диффузии, g — вектор ускорения свободного падения, γ — орт вертикальной оси z , η — динамическая вязкость смеси, p = pf [1+вс(C-Cl)] — плотность смеси, pf — плотность несущей жидкости при C = Cl = 0, βC — концентрационный коэффициент объёмного расширения примеси, α — коэффициент переноса, Kd — коэффициент, пропорциональный отношению скоростей адсорбции и десорбции примеси, Q0 — максимально возможная концентрация немобильных частиц, которые могут быть захвачены пористой средой [6].

Следуя [15], введём масштабы: для длины — H; для времени — H2/(Dф01); для скорости фильтрации — Dф01 /Н; для концентрации мобильной фазы — (Cu — Cl) = C0; для концентрации немобильной фазы — Q0; для давления — (цDф01)/K(ф01). В безразмерной форме уравнения (1)-(7) приобретают вид в каждом i-м подслое [15]:

uJ        (3 — Ф i Ф o1 )

—VP i — R p C i y ,

n i [ ' Ф i ^{Q i} (1 — Ф i ф 01 )

div U i = 0,                                                  (9)

Φ i ϕ 01

∂Ci    ζ ∂Qi dt + ФiCo dt

+ ( U i V )C i = Ф i ЛC i ,

^Q = a(1—Qi)Ci — bQi,

∂t а соответствующие граничные условия будут выглядеть так:

z = 0: Ci =0, Uiz = 0, z = S:  Uiz = U2z, Pi = P2, Ci = C2, Ф1Vz Ci = Ф2Vz C2,(13)

z = 1: C2 = 1, U2z = 0.

В (8) – (14) использованы следующие обозначения:

П = / 1, i = 1,       Ф 1, i = 1,

П I Kr, i = 2,    Фi 1 фг, i = 2, где i = 1 отвечает нижнему подслою, i = 2 — верхнему подслою. и параметры: Rp = pf всgHK(ф01) C0 /(nDф0i) — концентрационное число Релея-Дарси, определённое по параметрам нижнего подслоя 1; фг = ф02/ф01— отношение пористостей незагрязнённых подслоёв; Kr = K02 /K01 — отношение проницаемостей незагрязнённых подслоёв; a = [аКаН2C0) /(Dф01) — коэффициент адсорбции; b = [аН2) /(Dф01) — коэффициент десорбции; Z = Q0/Ф01 — коэффициент засорения пористой матрицы; 8 — параметр, показывающий положение границы раздела подслоёв.

Уравнения (8) - (14) написаны в предположении слабой закупорки пор, при которой Z / Ф 0 <<  1 и Z / C 0 ~ 1 В этом случае отношение проницаемостей загрязнённых и незагрязнённых i -х пористых подслоёв К ( ф _i )/ К (ф _{o i} ) , учитывающее зависимость ф _i = ф _{o i} [1 — (Z / Ф _i ) Q _i ] , можно разложить в ряд Тейлора [15] :

ζ

К ( ф ф )/ К ( фоф « 1 - ф-Q i

(3 - Ф i ф o1 )

^{(1 —ф} i ^ф 01 )

Основное или базовое течение в отсутствие концентрационной конвекции представляет собой сквозное плоскопараллельное течение Пуазейля в пористой среде при наличии постоянного продольного градиента давления V x P = — B , где B — положительная константа- В безразмерном виде этот градиент имеет вид: V x P = — Pe p , где Pe p = BHK _0i /( nDф _0i ) — число Пекле- Учитывая, что базовые профили концентрации зависят от поперечной координаты z (это следует из условия равновесия VC i х Y = 0 [1, 2] ), запишем уравнения конвекции в каждом i -м пористом подслое:

и граничные условия:

т.

U ix Π i

^Q ^{(3 — ф} i ^ф 01 )

Ф^¹ (1 — Ф i ф o1 )

= Ре

^{1 e} p ,

v2 C=о, a (1—Qi) Ci—bQi=0, z = 0: Ci = 0,

_      Л      Л               A                 A                A z = 8: Pi = P2, Ci = C2, Ф1 VzCi = Ф2Vz C2, z = 1: C2 = 1.

Из решения системы уравнений (16) – (18) с граничными условиями (19) – (21) получим базовые профили концентрации мобильной фазы в нижнем и верхнем подслоях:

C i (z) =

Ф 2 /Ф 1 ------------------£ ( Ф 2 / Ф 1 ) 8 +(1 — 8) ,

C 2 ( z ) =

( z — 1) (Ф 2 /Ф 1 )8 +(1 — 8)

+1 ,

а также профили продольной скорости и концентрации немобильной фазы в каждом i -м подслое:

т

U ix ^(z) — ^Pe p ⁿ i

ζ

¹⁺ ф Q

(3 — Ф i ф oi )

(1 — Ф i ф oi )

Q i ( z ) =

aC i (z) ai(z) + b

Далее будем рассматривать ситуацию, когда ф ₀₁ = ф ₀₂ = 0,4 и Ф _i = 1 - Незагрязнённые подслои имеют одинаковую пористость, характерную для сыпучих пористых сред (например, плотно упакованных шаров [2] ), однако могут отличаться проницаемостью. Это возможно, так как формула Кармана–Козени для нахождения проницаемости содержит два параметра: пористость и средний размер (диаметр) твёрдых включений [2, 24] . Для удобства представления и анализа результатов дополнительно введём концентрационные параметры: число Релея-Дарси R m = p f в с дНК _От C 0 /( nDф _0m ) ичислоПекле Pe m = BHK _{0 m} /(nDф _{0 m} ) ,определённыепосредней пористости ф _0т = 8ф ₀₁ + (1 — 8)ф ₀₂ и проницаемости К _0т = 8К ₀₁ + (1 — 8)К ₀₂ незагрязнённых подслоёв:

R m =R p

8+(1 — 8)К г

8+(1 —8' ) ф г ’

Pe m = Pe

p

5+(1 - 3)K r 3 +(1 — 3)ф г

Отметим, что для описания фильтрации смеси в двухслойной пористой среде применяется модель Дарси [2] . Известно, что она хорошо работает при числе Рейнольдса Re = ( p f D _p U x )/ n ^ 2,3 , где для оценки скорости фильтрации U x ^ Pe _p П _г [ Dф ₀₁ / H ] можно применить формулу (24) с учётом выбранного масштаба Dф ₀₁ / H [25] . Используя полученное выражение для скорости фильтрации, запишем число Рейнольдса через число Пекле Pe m , заданное формулой (27) , в виде:

Re =

D p Pe m      П _г

H Sc m { 3+(1 — 8 ) K r }

D p H

Pe em cm

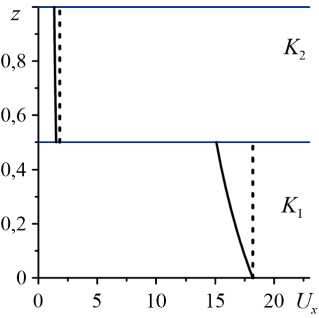
где Sc m = n /( P f Dф _0m ) — число Шмидта, определённое по средней пористости подслоёв ф _0т = 3ф ₀₁ + (1 — 3) ф ₀₂ . Для среды, состоящей из плотно упакованных сфер (шаров) и насыщенной водным раствором соли, число Пекле можно оценить как Pe m <  2,3Sc _m H / D p ^ 230 , где кинематическая вязкость n / P f ~ 10 ^{- 6} < 2/ A , коэффициент диффузии D = 14,6 см 2 /час, отношение толщины среды к диаметру сфер H / D p = 16 [14] . Выбранные параметры соответствуют данным эксперимента [14] . В настоящей работе используется диапазон чисел Пекле от 0 до 50. На рисунке 2 представлены базовые профили продольной скорости при a = 1,5 , b = 4 , C ₀ = 0,10 , Pe m = 10 для двухслойной пористой среды с 3 = 0,5 и K _r = 0,1 или K _r = 10 в отсутствие ( Z = 0 ) и при наличии закупорки ( Z = 0,3 ). В отсутствие закупорки скорость прокачки бинарной смеси в каждом из двух пористых подслоёв постоянна и не зависит от вертикальной координаты z . Значения скоростей в пористых подслоях разной проницаемости K 1 и K 2 отличаются главным образом в K r раз (см. формулу (28)). При наличии закупорки профиль скорости искажается, скорость уменьшается с ростом вертикальной координаты, поскольку вблизи верхней границы концентрация немобильной фазы максимальна, а вблизи нижней границы системы она принимает нулевое значение. Изменение скорости наиболее заметно в подслое с большей проницаемостью. Эта ситуация характерна для нижнего подслоя в среде с K r = 0,1 (см. Рис. 2а ), а для верхнего подслоя в среде с K r = 10 (см. Рис. 2б ).

( a )

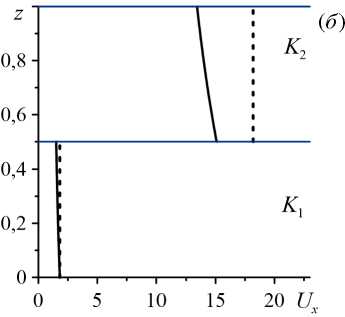
Рис. 2. Базовые профили продольной скорости в двухслойной пористой системе с при a = 1,5 , b = 4 , C 0 = 0, 10 , Pe m = 10 δ = 0,5 и разном отношении проницаемостей незагрязнённых подслоёв K r : 0,1 ( a ), 10 ( б ), в отсутствие закупорки ζ=0 (штриховые линии) ипри её наличии ζ = 0,3 (сплошные линии)

Определим значения критических параметров, при которых в системе возбуждается конвективное движение на фоне основного продольного потока. Для этого введём малые возмущения базового решения (22) – (25) , которые являются периодическими вдоль горизонтальной оси x с волновым числом к и инкрементом A = (A r — iu) , где A r — скорость нарастания ( A r > 0 ) или затухания ( A r < 0 ) возмущений, и — частота возмущений [5] :

(U i ,P i ,C ‘ ,Q i ) = (и i (z),P i (z),C i (z ),Q г (z))exp { A r t+ i ( kx — ut) } .                     (28)

Далее представим каждую переменную в виде суперпозиции ее базового решения (22) – (25) и возмущения (28) . Тогда получим систему уравнений для амплитуд возмущений в каждом i -м подслое:

Ш.

UU

(1 + A i Q г) +    A i Q г = ~^Р г — R p C i fl ,

Π i            Π i

41уиг = 0, и граничные условия:

^Ф - ^Ф 01 ^{( А} г ^{iw )}

z = 8 :

C i +

ζ

Ф i C ₀

~

Q i

U i V C i + lUi vj C i = ФЛС.

(A r -u C ) Q i — al 1 — Q i I C i — I aC i + b I Q i ,

z — 0:    C l —0,     U _1z —0,

Ulz — U2z ,    Pl — P2,    Cl — C2,    Ф1Vz Cl — Ф2Vz C2, z —1:    C2 — 0,    U2z —0,

где A i — Z (3 — Ф- Ф о1 )/[ Ф - (1 — Ф - Ф о1 )] .

Найдем границу устойчивости базового решения (22) – (25) относительно малых возмущений. Возмущения в этом случае не нарастают и не затухают, то есть A r — 0 . Далее, для удобства, можно применить стандартным образом [15] операцию rotrot z в проекции на ось z к уравнению (29) и исключить давление, а также переписать условие непрерывности нормальных напряжений P _l — P ₂ при z — 8, используя проекцию уравнения (29) на ось х .

Полученная краевая задача решается численно, способом построения фундаментальной системы решений [26] . Согласно этому способу, векторы решений Y _l — (U _{l z} , V _z U _lz ,C _l ,V _z C _l ) и Y ₂ — (U _{2 z} , V _z U _2z ,C ₂ ,V _z C 2 ) краевой задачи, относящиеся к нижнему и верхнему пористым подслоям, соответственно, представляются в виде суперпозиций базисных линейно независимых векторов частных решений: Y _l — Р 2₌₁ a i A ^{( i )} и Y 2 — p 2= _l e i B ^{( i )} . Векторы A ^{( i )} удовлетворяют условиям на нижней границе ( z — 0 ) двухслойной пористой системы, а векторы B ^{( i )} — условиям на верхней границе ( z — 1 ). Для базисных векторов записывается система обыкновенных дифференциальных уравнений, которая интегрируется методом Рунге–Кутты–Мерсона 5-го порядка с автоматическим выбором шага. Точность решения составляет 10 ^{- 6} . После интегрирования и подстановки линейных комбинаций векторов частных решений в условия на границе раздела подслоёв ( z — 0 ) получается задача на собственные значения. Эти значения находятся численно, методом секущих, из условия равенства нулю детерминанта полученной системы алгебраических уравнений. Сходимость метода секущих определяется близостью начального значения к искомому корню уравнения. В результате расчётов становится известным критическое концентрационное число Релея-Дарси R m * , которое соответствует порогу возбуждения колебательной конвекции в виде валиковых структур с волновым числом k ∗ и частотой ω ∗ .

• 3.    Численные результаты

  • 3.1.    Однослойная и двухслойная пористые среды в отсутствие закупорки. Предельные случаи

В отсутствие закупорки ( Z — 0 ) решение линейной задачи устойчивости горизонтального сквозного течения, вызванного постоянным градиентом давления V x P — — Pe p , в однородном пористом слое представляет собой критическое концентрационное число Релея–Дарси для порога возбуждения колебательной конвекции (см. [5] для концентрационной конвективной задачи и [3] — для тепловой конвективной задачи):

R m * —4П ² ,                                           (36)

с частотой критических возмущений

w * — к * Ре т /ф о ,                                           (37)

где критическое волновое число возмущений равно к * — п , а ф ₀₁ — ф ₀₂ = ф ₀ .

Концентрационная конвекция выглядит как естественные двумерные подъёмно-опускные валиковые структуры, которые возникают на фоне вынужденного продольного основного течения. Продольное течение поддерживается постоянным градиентом давления V x P — — Pe p . Оно сносит валиковые структуры вдоль по координате x , в итоге формируется колебательная конвекция.

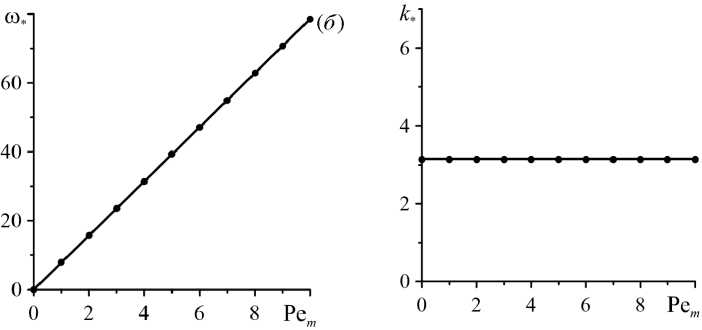
Полученные в работе данные демонстрируют хорошее количественное согласование с результатами (36) и (37) , к которым в обсуждаемой задаче можно прийти в следующих трёх предельных случаях (Рис. 3) :

• -    одинаковая проницаемость подслоёв ( K _r — 1 , любое 8 );

• -    толщина верхнего подслоя 2 равна полной толщине двухслойной системы ( 8 — 0 , любое K r ); - толщина нижнего подслоя 1 равна полной толщине двухслойной системы ( 8 — 1 , любое K r ). Численное решение отражает все три предельных случая.

Ниже, на рисунке 4, представлены результаты анализа устойчивости продольного потока, направленного по оси x , к повышению неоднородности концентрации примеси в двухслойной системе в отсутствие закупорки.

( a )

40 ^...........

0 4—•—।—•—।—■—।—■—।—>—।

0    2    4    6    8 Pew

( в )

Рис. 3. Предельные случаи зависимости от концентрационного числа Пекле концентрационных параметров конвективной устойчивости продольного основного течения в однородном пористом слое в отсутствие закупорки: число Релея–Дарси ( a ), частота ( б ) и волновое число ( в ) наиболее опасных возмущений основного течения; точками показаны данные, рассчитанные по аналитическим формулам (36) и (37) , линиями – численные результаты

Эта неоднородность изменяется путём увеличения концентрации примеси вблизи верхней границы системы, вблизи нижней границы системы концентрация примеси нулевая. Видно, что зависимости критического концентрационного числа Релея–Дарси, частоты и волнового числа наиболее опасных возмущений основного потока от отношения проницаемостей обладают зеркальной симметрией относительно линии K _r = 1 , то есть случая, когда двухслойная система сводится к одному слою с одинаковыми по всей толщине фильтрационными свойствами пористой среды. Наличие зеркальной симметрии обусловлено равной исходной пористостью (до закупорки) верхнего и нижнего подслоёв и линейным базовым профилем концентрации в них.

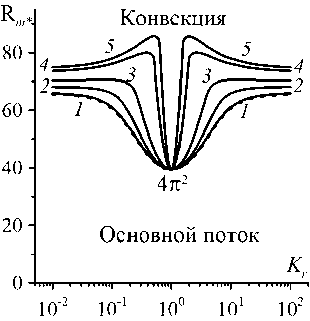
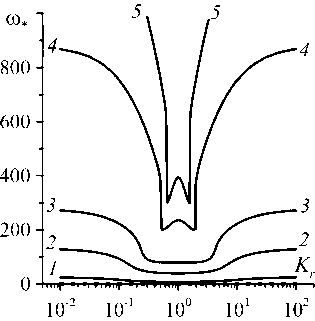
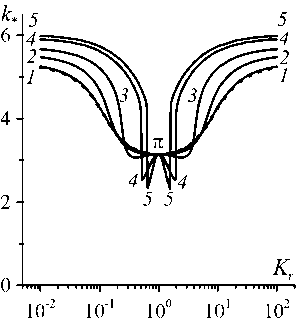
Согласно рисунку 4 a , влияние скорости продольного потока на его конвективную устойчивость наблюдается во всём диапазоне значений отношения проницаемостей, кроме K _r = 1 . Причём с ростом числа Пекле Pe _m устойчивость исходного состояния жидкости к концентрационным неоднородностям повышается. Критическое пороговое число Релея–Дарси быстрее растёт с изменением Pe m при мало отличающихся проницаемостях (не более чем в 10 раз). Это приводит к появлению экстремумов в зависимостях (см. Рис. 4) . На графиках зависимости R m ∗ от K r (Рис. 4a ) чётко выраженный максимум наблюдается при числах Pe m , больших 10, а точка этого максимума по оси K _r смещается к значению K _r = 1 с ростом Pe _m . На графиках зависимостей ω _∗ и k _∗ от K _r (Рис. 4б , в ) с повышением числа Pe _m образуются минимумы, вблизи которых по оси K _r происходит скачок ω _∗ и k ∗ . Например, при Pe m = 50 скачок приводит к двукратному изменению критического волнового числа и частоты возмущений при незначительном изменении отношения проницаемостей.

Наличие скачка критических параметров при изменении отношения проницаемостей указывает на смену вида естественных конвективных структур, возникающих пороговым образом. В двухслойной системе возможно возбуждение крупномасштабной (охватывающей оба подслоя) или локальной (возникающей в пределах одного

( a )

( в )

Рис. 4. Карты устойчивости – зависимости от отношения проницаемостей пористых подслоёв концентрационных параметров конвективной устойчивости продольного основного течения в двухслойной системе с пористыми подслоями одинаковой толщины ( 5 = 0,5 ): число Релея-Дарси ( a ), частота ( б ), волновое число ( в ) наиболее опасных возмущений основного течения; в системе отсутствует закупорка, число Пекле Pe m принимает значения: 0 (штриховая линия), 1 (сплошная линия 1 ), 5 ( 2 ), 10 ( 3 ), 30 ( 4 ), 50 ( 5 )

из подслоёв) валиковых структур течений. При нулевом или слабом продольном вынужденном потоке жидкости (при Pe m < 10 ) переход от крупномасштабной к локальной конвекции с усилением различия в проницаемостях подслоёв происходит постепенно, без скачка критических параметров (см. кривые 1 – 3 , Рис. 4б , в ). При сильном продольном течении (при Pe m > 10 ) переход к локальной конвекции с увеличением отклонения K r от единицы становится скачкообразным (см. кривые 4 – 5 , Рис. 4б , в ).

Возникновение разрыва с ростом числа Pe m в зависимостях критических характеристик ( w _t и к * ) колебательного течения можно объяснить противоположным действием вынужденного продольного потока на крупномасштабную и локальную фазы конвекции. Если в системе с потерей устойчивости продольного потока жидкости возбуждается колебательное крупномасштабное, имеющее валиковую структуру течение, то появление основного вынужденного течения и рост его интенсивности не только приводит в движение по продольной координате конвективные валы, но и увеличивает их горизонтальный размер. Этот вывод подтверждает график на рисунке 4в , на котором область крупномасштабной конвекции находится в окрестности симметрии системы K r = 1 . В указанной области волновое число к * уменьшается с ростом числа Pe m , что соответствует увеличению длины волны, характеризующей горизонтальный размер конвективных валиков (Рис. 5) . Если в системе с потерей устойчивости продольного потока жидкости возникает естественная конвективная, то есть преимущественно локализованная в пределах одного из подслоёв валиковая структура, то увеличение числа Pe _m приводит к противоположному, по сравнению с крупномасштабной конвекцией, эффекту: с ростом числа Pe _m горизонтальный размер конвективных валиков не увеличивается, а уменьшается. На рисунке 4в этот эффект наблюдается при значениях K r , на порядок или более отличающихся от единицы.

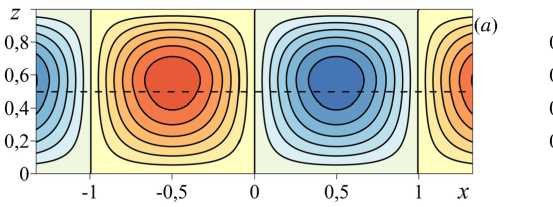
Рис. 5. Линии тока валикового конвективного течения при K r = 1,5 в отсутствие закупорки при разных значениях числа Пекле Pe m : 0 ( а ), 50 ( б )

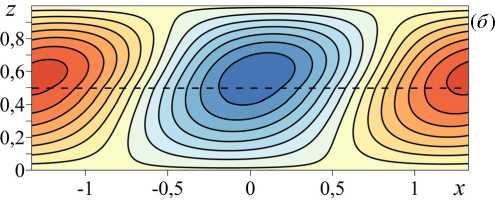
Следует отметить, что в отсутствие закупорки пористость верхнего и нижнего подслоёв одинаковая, следовательно, градиенты концентрации в подслоях, которые могут быть оценены по формулам (22) и (23) , также имеют одинаковые значения. При данных условиях после перехода от крупномасштабной конвекции колебательное конвективное течение локализуется преимущественно в пределах подслоя с большей проницаемостью вне зависимости от его расположения (сверху или снизу). При анализе влияния закупорки на устойчивость вынужденного продольного потока жидкости в двухслойной пористой среде, который осуществляется далее, этот факт будет учтен.

• 3.2.    Влияние числа Пекле на параметры системы при наличии закупорки

Рассмотрим две двухслойные системы со значениями отношения проницаемостей незагрязнённых подслоёв 0,1 и 10. Первое значение соответствует двухслойной пористой системе, в которой высокопроницаемый подслой находится снизу, а второе значение — системе с высокопроницаемым подслоем, расположенным сверху. В первой системе колебательная конвекция возникает в пределах нижнего подслоя (см., Рис. 6) , а во второй системе — в пределах верхнего подслоя (см. Рис. 7) . Значения K r выбраны симметричными относительно линии K r = 1 графиков рисунка 4. Ввиду симметрии решений для обеих систем в отсутствие закупорки получаются одинаковые зависимости критических параметров ( R m * , ш * и к * ) от числа Pe m (штриховая и сплошная линии 1 , Рис. 8) . Количественно закупорку порового пространства среды характеризует коэффициент засорения £ .

Для анализа влияния закупорки на конвективную устойчивость приведём результаты расчётов, полученные для Z = 0,1 . Как видно из рисунка 8 a , закупорка в целом приводит к росту критического порогового числа R _m ∗ . Чем больше коэффициент засорения, тем существеннее повышается устойчивость продольного потока жидкости к концентрационным неоднородностям примеси. Кроме повышения устойчивости, закупорка приводит к нарушению симметрии решений относительно линии K r = 1 . На рисунке 8а видно, что зависимости порогового числа R _m ∗ от числа Pe _m при одном и том же значении коэффициента засорения различаются. Причём для двухслойной системы кривая R m * (Pe m ) при верхнем высокопроницаемом подслое (K r = 10 ) лежит

( a )

( б )

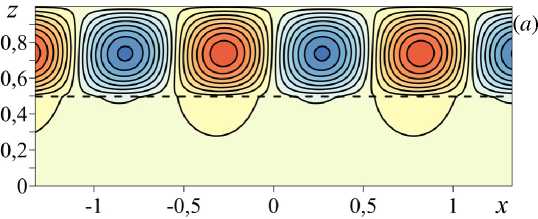
Рис. 7. Линии тока конвективного валикового течения в двухслойной системе с K r = 10 и Pe m = 50 и различным коэффициентом засорения ζ : 0 ( а ) и 0,3 ( б )

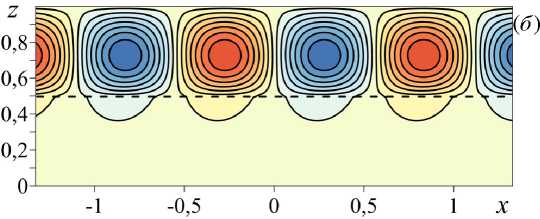
Рис. 6. Линии тока конвективного валикового течения в двухслойной системе с K r = 0,1 и Pe m = 50 и различным коэффициентом засорения ζ : 0 ( а ) и 0,3 ( б )

( a )

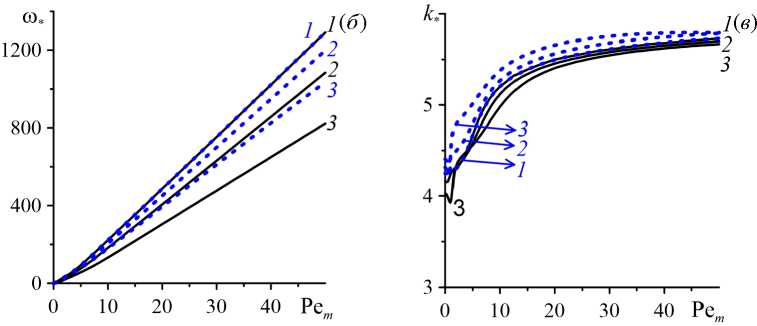
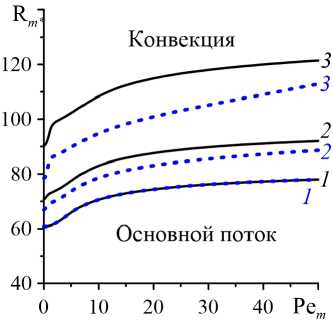
Рис. 8. Зависимости от концентрационного числа Пекле параметров конвективной устойчивости продольного основного течения: критическое концентрационное число Релея–Дарси ( a ), частота ( б ) и волновое число ( в ) наиболее опасных возмущений основного течения, в двухслойной системе c пористыми подслоями одинаковой толщины ( δ = 0, 5 ) в отсутствие и при наличии закупорки с a=4 , b=4 , C 0 =0,1 и K r =0,1 (штриховые линии) или K r = 10 (сплошные линии) и различными значениями коэффициента ζ : 0 (линии 1 ); 0,1 ( 2 ); 0,3 ( 3 )

выше аналогичной зависимости при нижнем высокопроницаемом подслое (K r = 0,1 ) при обоих значениях коэффициента засорения ( Z = 0,1 и Z = 0,3 ). Нарушение симметрии решений относительно K r = 1 возникает из-за появления неоднородности пористости вдоль поперечной координаты z . Эта неоднородность пористости обусловлена зависимостью концентрации немобильной фазы примеси от z . Из формулы (25) можно увидеть, что концентрация немобильной фазы растет вместе с увеличением концентрации мобильной фазы. Согласно постановке задачи, концентрация мобильной фазы примеси линейно меняется от нулевого значения вблизи нижней границы по направлению к фиксированному значению C 0 вблизи верхней границы двухслойной системы. Таким образом, в среднем по подслою концентрация мобильной и немобильной фаз примеси всегда выше в верхнем подслое, чем в нижнем. Поскольку колебательная валиковая конвекция в рассматриваемых двухслойных системах возникает преимущественно в пределах высокопроницаемого подслоя, тогда и влияние на побуждение этой конвекции будет сильнее в случае, когда высокопроницаемый подслой располагается сверху ( K _r = 10 , Рис. 7) , где за счёт закупорки пористость и проницаемость уменьшаются сильнее.

Нарушение симметрии решений, которое описано выше, отражается и на характеристиках колебательного течения. На рисунке 8б , в видно, что при Z = 0,1 (линии 2 ) и Z = 0,3 (линии 3 ) штриховые линии не совпадают со сплошными линиями с такими же с номерами. На рисунке 8в приведены зависимости волнового числа наиболее опасных возмущений от числа Pe m . Закупорка слабо влияет на волновое число к * , так как кривые k * (Pe m )

при закупорке (штриховые и сплошные линии 2 , 3 , Рис. 8в ) с небольшими отклонениями повторяют кривую k _∗ (Pe _m ) без закупорки (штриховая и сплошная линии 1 , Рис. 8в ). В целом критическое волновое число k _∗ сначала увеличивается с ростом Pe _m , а затем при его больших значениях ( Pe _m > 20 ) выходит на величину k _∗ ≈ 5,6 и при дальнейшем росте Pe _m практически не меняется. В свою очередь закупорка приводит к существенному уменьшению частоты критических возмущений ω _∗ . Например, уменьшение частоты в двухслойной пористой среде с верхним высокопроницаемым подслоем ( K _r = 10 ) при коэффициенте засорения ζ = 0,3 (сплошная линия 3 , Рис. 8б ) может достигать 40% относительно значения частоты в отсутствие закупорки (линии 1 , Рис. 8б ). Существенное уменьшение частоты ω _∗ при практически не меняющемся волновом числе k _∗ указывает на уменьшение скорости ω _∗ /k _∗ распространения валиковых конвективных течений вдоль координаты x . Так как за счёт закупорки при линейно растущей концентрации мобильной фазы примеси вдоль поперечной оси z пористость в верхнем подслое в среднем понижается заметнее, чем в нижнем подслое, то наибольшее замедление движения локализованных в пределах высокопроницаемого подслоя конвективных валов будет происходить в двухслойной пористой среде с K r = 10 , в которой высокопроницаемый подслой находится сверху.

• 3.3.    Влияние коэффициентов адсорбции и десорбции на параметры системы

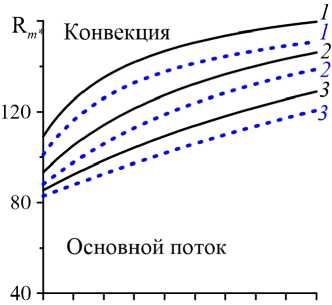
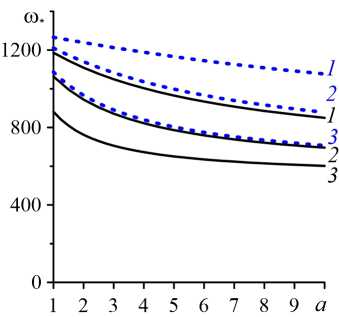
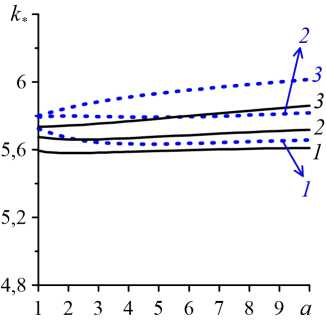
Коэффициенты адсорбции a и десорбции b — это материальные параметры, зависящие от вида примеси и текущей внутри двухслойной системы жидкости. Они характеризуют взаимообратные процессы. Увеличение коэффициента адсорбции повышает объёмную долю немобильной части примеси относительно мобильной, а увеличение коэффициента десорбции приводит к обратному эффекту. На рисунке 9 представлены результаты расчётов критических параметров ( R _m ∗ , ω _∗ и k _∗ ) колебательного конвективного течения для следующих значений коэффициентов a и b : a = 1, ..., 10 ; b = 1,5; 4; 10 . При этом число Pe _m и коэффициент засорения ζ равны, соответственно, 50 и 0,3, а колебательное конвективное валиковое течение локализуется преимущественно в высокопроницаемом подслое (в верхнем подслое в системе с K _r = 10 ; в нижнем подслое в системе с K _r = 0,1 ). Конвективная устойчивость продольного основного течения согласно результатам, представленным на рисунке 9a , с ростом коэффициента адсорбции повышается. Изменение коэффициента десорбции в большую сторону дестабилизирует основное течение, поэтому здесь кривые зависимостей R m ∗ (a) , построенные при больших коэффициентах десорбции, лежат ниже кривых с меньшими значениями этого коэффициента. Согласно графику на рисунке 9в , зависимость критического волнового числа k ∗ от сорбционных процессов слабая. Относительное отклонение от среднего значения волнового числа при взятых в расчёт величинах коэффициентов a и b не превышает 4%. При этом относительные изменения частоты ω ∗ критических возмущений на порядок больше отклонений волнового числа. Это позволяет говорить о практически прямой пропорциональности между частотой и скоростью распространения конвективных валиковых течений вдоль координаты x . Таким образом, если на графике ω _∗ (a) (см. Рис. 9б ) присутствует нисходящая линия, то так же выглядит и зависимость скорости перемещения конвективных валиков ω _∗ /k _∗ , то есть они замедляют своё движение с ростом коэффициента a . Причиной такого постепенно усиливающегося адсорбционного процесса может быть рост концентрации немобильной фазы в подслое с колебательным течением относительно мобильной части примеси. Нарастающая немобильная фаза уменьшает пористость и проницаемость подслоя. Необычный эффект имеет место при

12 3 456789a-

( в )

Рис. 9. Зависимости от коэффициента адсорбции параметров конвективной устойчивости продольного основного течения: число Релея–Дарси ( a ), частота ( б ), волновое число ( в ) наиболее опасных возмущений основного течения, в двухслойной системе c пористыми подслоями одинаковой толщины ( δ = 0,5 ) при наличии закупорки ζ = 0,3 с C 0 = 0,1 , Pe m = 50 и K r = 0,1 (штриховые линии) или K r = 10 (сплошные линии) и различными значениями коэффициента десорбции b : 1,5 (линии 1 ), 4 ( 2 ), 10 ( 3 )

усилении десорбционного процесса за счёт увеличения коэффициента b. На первый взгляд усиление десорбции должно приводить к уменьшению концентрации немобильной фазы, повышению пористости и проницаемости, и как следствие, к увеличению частоты и скорости конвективных подъёмно-опускных течений. Но, согласно расчётам, результаты которых представлены на рисунке 9б , наблюдается обратная тенденция. Рост коэффициента b приводит к уменьшению частоты колебательной конвекции, а не к ее увеличению.

• 4.    Заключение

Изучена конвективная устойчивость плоскопараллельного продольного течения в системе, находящейся в поле силы тяжести и состоящей из двух горизонтальных пористых подслоёв с разными проницаемостями. Задача рассмотрена в изотермических условиях при постоянно поддерживаемой концентрации примеси на верхней границе и нулевой концентрации на нижней границе системы. В рамках сплошной среды и с использованием нелинейной MIM-модели, в которой применяется деление примеси на мобильную и немобильную, выведена система дифференциальных уравнений конвекции. Расчёты проведены при равных исходных пористостях подслоёв, но разных проницаемостях. Найдены и сопоставлены между собой базовые профили горизонтальной скорости в отсутствие и при наличии засорения порового пространства. Выполнен линейный анализ устойчивости основного течения. Проведено численное моделирование краевой задачи способом построения фундаментальной системы решений. Получены нейтральные кривые устойчивости горизонтального плоскопараллельного сквозного течения относительно малых возмущений в виде валов с разной длиной волны. Определены минимальные значения числа Релея–Дарси, соответствующие порогу возникновения колебательной конвекции, для каждой нейтральной кривой. В отсутствие засорения построены карты конвективной устойчивости вынужденного плоскопараллельного течения в координатах числа Релея–Дарси и отношения исходных проницаемостей незагрязнённых подслоёв, которые показывают повышение устойчивости равновесия при увеличении числа Пекле Pe m . Проанализированы найденные зависимости частоты и волнового числа критических возмущений от отношения проницаемостей для нескольких значений числа Pe m , взятых из диапазона от 0 до 50. Эти результаты обладают симметрией относительно значения отношения проницаемостей, равного единице. Наличие симметрии обусловлено одинаковой пористостью незагрязнённых верхнего и нижнего подслоёв и линейным базовым профилем концентрации в них. Зафиксировано появление скачка при числе Pe m > 10 в критических характеристиках конвективного течения при изменении отношения проницаемостей, который указывает на резкий переход от крупномасштабной, охватывающей оба подслоя, к локальной, возникающей в пределах одного из подслоёв, валиковой структуры течения.

Влияние засорения, связанного с адсорбцией и десорбцией примеси в пористых подслоях, исследовано в двух двухслойных системах со значениями отношения проницаемостей подслоёв 0,1 и 10. В первой двухслойной системе высокопроницаемый подслой находится снизу, а во второй системе высокопроницаемый подслой располагается сверху. Для этих систем построены зависимости критического порогового числа Релея–Дарси, частоты и волнового числа наиболее опасных возмущений от числа Пекле для значений коэффициента засорения 0,1 и 0,3. Обнаружено, что засорение повышает устойчивость продольного основного потока жидкости к концентрационным неоднородностям примеси и нарушает симметрию решений относительно случая, когда двухслойная система сводится к одному слою с одинаковыми по всей толщине фильтрационными свойствами пористой среды. Далее для числа Pe m = 50 и коэффициента засорения Z = 0,3 изучено влияние коэффициентов адсорбции и десорбции на критические параметры колебательного конвективного течения. Проанализированы графики критического числа Релея–Дарси, частоты и волнового числа возмущений от величины коэффициента адсорбции для значений коэффициента десорбции: 0,15; 4; 10. Для оценки структуры конвективного течения построены изолинии функции тока. Зафиксирована слабая зависимость характерных размеров локальных конвективных валиковых течений от параметров засорения (коэффициента засорения или параметров адсорбции и десорбции). Показано, что сорбционные процессы, которые могут приводить к засорению, существенно изменяют частоту критических возмущений, а значит и скорость конвективных валиковых структур, движущихся колебательным образом вдоль двухслойной системы. Например, засорение при Z = 0,3 уменьшает скорость движения валов в двухслойной системе с K r = 10 почти на 40%.

Исследование выполнено за счёт гранта Российского научного фонда, проект № 20-11-20125 20125/).