Общие математические модели законов диалектики

Современные философы по-разному относятся к законам диалектики Гегеля: от полного их признания до полного отрицания [1, 2]. Поэтому, чтобы не вдаваться в философские дискуссии, мы попытаемся построить общие математические модели этих законов для некоего виртуального мира, предполагая то, что диалектика этого мира основана на гегелевских положениях.

Модели законов диалектики Гегеля

Будем предполагать, что процесс развития описывается вектором X ( t ) функций x ₁( t ),..., x_n ( t ) , т. е.

X (t) =(x 1(t)-, xn (t)) , причем     справедливо     соотношение

n

У x ² ( t ) * 0 , где t - время.

i = 1

Пусть направление развития процесса задает вектор A , где

A = ( a j,..., a_n ), a_t = const , a_t * 0, i = 1, n .

Согласно закону единства и борьбы противоположностей Гегеля, можно заключить, что развитие процесса идет в ходе этой борьбы, поэтому среди компонент вектора A существуют такие компоненты, что выполняется условие

3 i , 3 j : a^ <  0, i = 1, n , j = i + 1, n .

Отметим, что также должно быть справедливым соотношение

n

У a = 0, i=i которое говорит о единстве противоположностей.

Очевидно, что компоненты вектора A являются своеобразными весовыми коэффициентами, определяющими значимость каждой противоположности в общем развивающемся процессе. Чем больше модуль компонента, тем выше значимость противоположности. Если расположить элементы вектора в неубывающем порядке, то легко видеть, что для весовых коэффициентов должны выпол- няться равенства

n ₁

У a, =-1 для ai < 0 и i=i

n

У a; = 1 для ai > 0 , где nj - количество i=n +1

отрицательных компонент вектора A , n — n - количество положительных компонент вектора A , n_x >  1, n >  n_x .

Следует отметить, что согласно свойствам векторов все компоненты векторов X ( t ) и A должны измеряться в одинаковых единицах измерения и иметь одинаковый "физический" смысл.

В работах [3, 4] предложен способ, позволяющий численно оценивать величину достижения цели в ходе воспитательного процесса. Способ, предложенный в этих работах, также позволяет вычислять угол отклонения от цели воспитательного процесса. В аспекте моделирования диалектических законов Гегеля мы, модифицируя способ, будем предполагать, что цель процесса развития определяется вектором A направления этого развития. Тогда, не нарушая общности, можно заключить, что успешность развития процесса определяется математической зависимостью F (t ) , являющейся отношением проекции вектора X ( t ) на вектор A к длине вектора A . Таким образом, на основе правил векторной алгебры [5] становится справедлива формула

T axi ⁽ t )

F ( t ) =     -------.             (1)

Е a. i = 1

Будем считать, что процесс развивается успешно на интервале времени ( t ₀, T ) в направлении, заданном вектором A , если на этом интервале F ( t ) является монотонно возрастающей функцией. В предположении дифференцируемости функций x_x (t ), i = 1, n при t е ( t₀ .T ) , применяя теоремы математического анализа, описывающие свойства монотонных дифференцируемых функций [6], успешность, неуспешность или застой процесса развития можно отобразить следующей таблицей.

Условия протекания процесса

Выполнение условия	Развитие процесса
Yadx^ >  0 h i dt	Развитие процесса идет в заданном вектором A направлении
fadxM . 0 £ i  dt	Развитие процесса характеризуется застоем
Y^x^ <  0 h i dt	Развитие процесса идет в противоположном вектору A направлении

На основе работ [3, 4] и свойств скалярного произведения векторов [5] угол отклонения Ф(t) процесса, характеризуемый векто ром X(t) , от направления развития A определяется функцией цикличности z (t) = cos(T( t)), задаваемой соотношением

n

Е a i x i ⁽ t )

z ( t ) = ^=L        ..     (2)

nn

Л Е < Е x2( t) zl

Принимая гегелевское положение закона отрицания отрицания о цикличности развития процессов, можно заключить, что колебательная функция z ( t ) определяет и описывает эту цикличность и борьбу противоположностей друг с другом.

Отметим, что зависимости F ( t ) и z ( t ) являются безразмерными.

Предполагая, что каждая из компонент

x; (t), i = 1, n является дифференцируемой функцией при t е (t0 .T), можно вычислить n dz (t)  _ а     __ производную      , значения которой опре- dt деляют скорость циклов в законе отрицания отрицания. Легко показать, что эта производная удовлетворяет соотношению dz (t) _ dt dx (t)     2 / \ v             / dXx> (t)

, Е a       Е ^x i ⁽ t ) - Е axdt) E ^x i ⁽ t )

_      ¹       i = 1        ^dt i = 1 i = 1 i = 1 ^dt

Согласно Гегелю необходимым условием развития является цикличность, т. е. функция z(t) = cos(^(t)) должна менять свои свойства: то становиться возрастающей, то убывающей, что эквивалентно свойству зна-dz (t)  ~ копеременности функции      . Последнее dt уже накладывает ограничения на общие математические свойства противоположных друг другу процессов виртуального мира.

Так как согласно Гегелю для развития должны существовать как минимум два противоположных друг другу процесса, количе ство компонент в векторах A и X(t) должно быть не меньше двух.

Докажем это утверждение математически.

Согласно Гегелю для развития должна быть цикличность, т.е. должна быть справедлива формула z ( t ) ^ const при t е ( t₀ .T ) .

Пусть только один процесс характеризует развитие. В этом случае справедливо соотношение n = 1.

Подставляя значение n = 1 в соотношение (2) после несложных алгебраических преобразований      получим      равенство

z(t ) = cos ^ ( t ) = 1 = const , т. е. функция цикличности не является знакопеременной.

Таким образом, мы доказали, что для описания процесса развития должно быть справедливо соотношение n >  2 .

Покажем, что для развития противоположные друг другу процессы не должны быть полностью эквивалентными друг другу.

Докажем это методом "от противного". Пусть два противоложных процесса эквивалентны друг другу, т. е. обладают свойствами, определяемыми соотношениями n = 2, A = (1,-1), Xi (t) = x2 (t), t e(t0, T).

Легко видеть, что согласно соотношениям (1) и (2) в этом случае развития нет, так как справедливы равенства F ( t ) = 0 и z ( t ) = 0 . Полученное противоречие доказывает утверждение.

Пример применения моделей

Рассмотрим пример практического применения приведенных выше положений на основе простой задачи классической механики.

Опишем динамику процесса вертикального подкидывания камня вверх с первоначальной скоростью v₀ с поверхности земли без учета сопротивления воздуха его движению.

Будем считать, что в этом процессе действуют две равноценных противоположности: перемещение X j ( t ) , направленное вертикально вверх, и перемещение x ( t ) , направленное вертикально вниз.

Так как противоположности равноцен ны, вектор A имеет вид A = (1, — 1). Следовательно, развитие процесса F(t) согласно соотношению (1) описывается формулой

F ( t ) = ^x . ⁽ t ) ^{— x} 2 ⁽ t ) .           (3)

Нетрудно заметить, что противоположность X j ( t ) определяется решением задачи Коши:

d ^ = 0, d ^  = v 0 , x , (0) = 0. (4)

dt             dt / 1 = 0

Противоположность X ( t ) описывается задачей Коши:

d ² x₂ ⁽ t )       dx₂ ⁽ t )

— --= g ,——   = ⁰, ^x 2 ⁽⁰⁾ = ° , (5)

dt              dt   / 1 = 0

где g - ускорение свободного падения.

В результате решения задач (4) и (5) получаем соотношения:

_ gt ²

^X 1 ⁽ t ) = v 0 t , ^X 2 ⁽ t ) = y.

Согласно равенству (3) развитие процесса выражается равенством

F (t) = — g- + vl t, 4     2  ’ т. е. параболической зависимостью, описывающей взлет камня с его последующим падением до начальной точки бросания.

Функция цикличности z(t) удовлетворяет соотношению z (t) =    — gt + 2 v 0    .

2,2

2y v 0 + у

На рис. 1, 2 и 3 приведены графики изменения каждой из противоположностей x ₁ ( t ) и x ₂ ( t ) , график развития процесса F ( t ) и график функции цикличности z ( t )

соответственно при v = 5    , единицах из-

0ñ мерения времени t в секундах, а x (t) и x (t) в метрах.

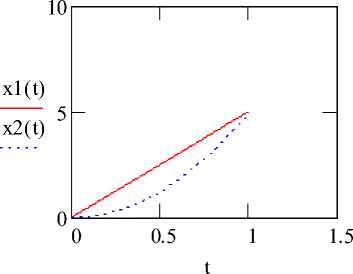
Рис. 1. Графики изменения противоположностей

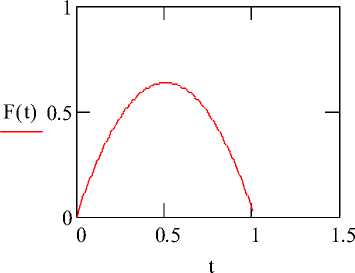
Рис. 2. График развития процесса

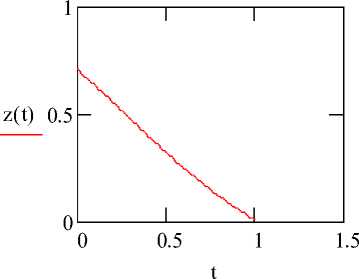
Рис. 3. График функции цикличности

На рис. 1 отражено, что с течением времени противоположности рассматриваемого процесса выравниваются, сглаживаются, а точка пересечения графиков х (t) и х2 (t) соответствует завершению рассматриваемого в примере процесса на рассматриваемом интервале времени. Анализ графика, изображенного на рис. 2, показывает, что развитие рассматриваемого процесса на этом же интервале со временем прекращается. График, изображенный на рис. 3, демонстрирует отсутствие цикличности, а значит, и яркого проявления в процессе на рассматриваемом интервале времени закона отрицания отрицания.

Алгоритм использования общих математических моделей законов диалектики

Исходя из написанного выше, можно предложить следующий алгоритм построения модели и анализа проявления законов диалектики виртуального мира:

• 1.    Определяются противоположные характеристики, входящие в описание процесса.

• 2.    Определяется вектор A , задающий направление развития процесса.

• 3.    Записываются соотношения, определяющие численные значения противоположных характеристик

• 4.    Для диалектического анализа процесса используются соотношения (1) и (2).

• 5.    При необходимости строятся графики противоположностей, развития процесса и функции цикличности.

xi (t), i = 1,n , участвующих в процессе.

Заключение

Таким образом, в настоящей статье предложены общие математические модели философских законов Гегеля. Эти модели могут применяться при численном анализе диалектических процессов, проходящих в некоем виртуальном, а возможно, и реальном окружающем нас мире.