Обучение школьников решению задач с помощью элементарных методов нахождения наибольших и наименьших значений величин

Современное образование предполагает развитие разносторонней личности. На уроках математики наиболее развиваются умения анализировать и применять рациональные методы при решении задач.

Задачи на нахождение наибольшего и наименьшего значения величин имеют не только прикладную значимость, но и практическую направленность. В школьном курсе данная тема рассматривается в основном в рамках теории производных в курсе алгебры, однако, есть и другие методы решения подобных задач, рассмотрение которых будут способствовать развитию аналитическое и творческого мышления обучающихся. В данной статье рассмотрим такой метод, как метод оценки.

Данный метод относится к геометрическим, что так же будет способствовать межпредметной связи геометрии и алгебры.

Метод оценки применяется для нахождения наибольшего или наименьшего значения при решении геометрической задачи, когда трудно или невозможно заметить граничные значения переменной величины, которая нас интересует. Тогда, может быть удобно выразить эту переменную через другие величины, среди которых есть переменная, граничное значение которой хорошо известно или его легко заметить.

Метод оценки очень часто применяется к тем задачам, в которых не ставится требование найти экстремальное значение, но при их решении такой вопрос возникает невольно.

Метод оценки помогает решить экстремальные задачи в неявном виде, которые возникают на одном из этапов решения задачи на построение, т.е. при исследовании (когда нужно оценить данные в условии величины, чтобы выяснить существование решения).

Объектом оценки может быть граничное значение расстояния, величина угла, значение площади. В некоторых задачах вместо переменного значения площади выступает значение тригонометрической функции.

Распространёнными задачами, в которых используются метод оценки, являются задачи с экономическим содержанием.

Задача : Для обеспечения населения города нужно закупить 3000т картофеля в 4 совхозах. Количество картофеля, которое может продать каждый совхоз, и цена перевозки показаны в таблице: [1]

Нужно разработать план закупки картофеля так, чтобы стоимость была наименьшей, и найти эту стоимость. Из таблицы видно, что закупку картофеля нужно определить ценой перевозки 1т (2; 2,5; 2,7; 3), которой соответствует такая последовательность: 800, 900, 700, 1100. Решение задачи сводится к оценке сумм:

• 1)    800 < 3000;

• 2)    800 + 900 = 1700 < 3000;

• 3)    1700 + 700 = 2400 < 3000;

• 4)    2400 + 1100 > 3000;

• 5)    3000 – 2400 = 600;

• 6)    800 х 2 + 900 х 2,5 + 700 х 2,7 + 600 х 3 = 7540 (руб.)

Обучающиеся, начиная с 5 класса встречают задачи, имеющие не одно, а несколько решений. В таком случае необходимо ставить вопрос о нахождении наиболее или наименее выгодного решения.

Таким образом, с помощью метода оценки, мы подготавливаем учащихся к изучению более сложных тем и решению более сложных задач.

Но не стоит думать, что метод оценки является лишь подготовительным к изучению понятия производная. Многие задачи на нахождение наибольших и наименьших значений величин рациональнее решить с помощью метода оценки.

Рассмотрим задачу, решаемую с помощью метода оценки, которая поможет учащимся увидеть рациональность и практическую направленность данного метода:

Задача : Расстояние от пункта А до пункта В 4 км , а от пункта В до С вдвое больше. Какое наибольшее и наименьшее расстояние может быть от пункта А до пункта С? [2]

Решение:

В первую очередь нужно заметить, что расстояние АС зависит от места расположения точки С. Так как расстояние ВС постоянное, то точка С принадлежит точкам окружности с радиусом ВС и центром В

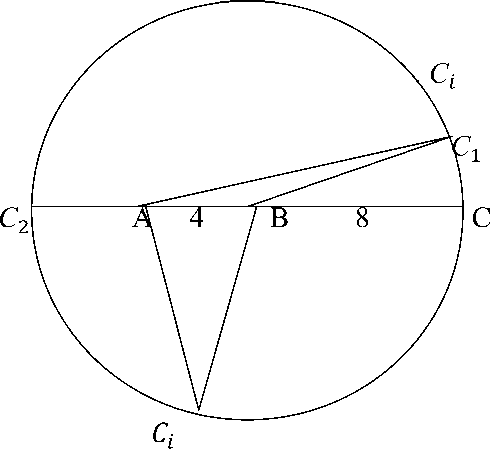
(рис.1)

Легко заметить, какие граничные значения переменная величина АС может принимать, 4 = АС ₂<  АС [ <  АВ + ВС [ =12.

Отсюда ясно, что АС наиб = 12 км, АС наим = 4 км.

Искомыми точками С _t являются концы диаметра длиной 16 км с центром окружности в пункте В.

Можно сделать вывод, что обучение элементарным методам нахождения наибольших и наименьших значений величин, в частности методу оценки, является важной частью обучения школьного курса математики, и необходимо более широко раскрывать возможности использования различных методов перед обучающимися, а не ограничиваться методом решения с помощью производной.