Оценка числа слагаемых нормальной аппроксимации сумм независимых случайных величин

Проблема оценки числа слагаемых, при котором сумма независимых случайных величин имеет нормальный закон распределения вероятностей, связана с центральной предельной теоремой (ЦПТ).

ЦПТ имеет особое место среди практических применений теории вероятностей. Она позволяет решать многие задачи в различных областях, где рассматриваются суммы случайных величин. Проблема распределения суммы случайных величин по нормальному закону решается в статьях [1; 2; 3] методом моделирования. В статье [1] получено, что при 30 и более слагаемых график плотности распределения близок к нормальному. В работе [2] указывается, что для нормально распределенной генеральной совокупности ЦПТ справедлива даже для выборок с объемом менее 30. Размер выборки 200 слагаемых использовался в работе [3].

Данное исследование является дальнейшим развитием метода из [4] определения числа слагаемых ЦПТ. Новым является распространение этого метода на случай разных значений средних квадратических отклонений [4].

Целью статьи является определение числа слагаемых ЦПТ для получения нормального закона распределения вероятностей с заданной точностью. Для этого нужно получить число n в виде его функциональной зависимости от параметров закона распределения суммы или средней выборочной.

1 Основная теорема и следствие

Сформулируем и докажем следующую теорему.

Теорема. Средняя выборочная (x) n независимых случайных величин с одинаковыми математическими ожиданиями m и разными дисперсиями, ограниченными сверху значением <гmax, будет иметь нормальный за кон распределения (с точностью £ ) при n > n 0 = max <

[ _v ⁴ .5 ° max J + ²,

^4,5 ^ max

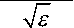
+ 1, L ^0,41 + ^Ь ° max J ” .

Здесь символом ^ J обозначена целая часть числа.

Доказательство.

Определим число n0 методом характеристических функций. Рассмот- рим непрерывные случайные величины.

Пусть

^qx j

—t

У ⁿ 0 J

« ‘^x j

= J e n ⁰ • ^f ( x ) dx ,

-to

характеристическая функция

Xj случайной величины —(j = 1, n0). Тогда n 0 x n 0

q ¹ t ⁾⁼ H q x ,

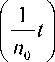
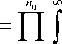
itx en 0

J = 1 -to

• ^f ( x ) dx j

характеристическая функция величины x , т. к. X _f независимы.

Не нарушая общности, считаем, что m = 0 . Разложим q_x

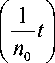
в ряд

i to                                  i

Маклорена. Получим: q_x ( 0 ) = 1; q_x ( 0 ) = — j x j f ( x j ) dx j = —m = 0. ^{j                  j n} 0 --to                          ⁿ 0

Вторая производная будет равна:

i ^{2 г}

2 ° j .

n ₀ ²

qXj^ 0 ) =   J Xf ( xj) dxi =

n 0 —г

Остаточная сумма ряда S_ост определяется выражением:

С учетом того, что q (0) = 1, она будет равна: Socm (0) = 0. Тогда qxj

— t | = 1

n о

—

2 n 0 ' * ° ' '

n ₀

qx (t)=П i—A • t"°,2

j — 1 к

Пусть выполняются следующие условия:

—3 • ° max

' max , при t ² = ⁹ • ° max ⁹ ' ° max

< 2 n 2 и скобки в (2) поло-

жительные. Заметим, что условие положительности скобок в (2) вытекает из условия n ₀ >  4,5 ° max . Поэтому

n о >  д/4,5 • ° ma _X.

Для дальнейших выводов будем считать, что

n ₀ >  max

Найдем логарифм от (2):

n ₀

ln q x ( t ) = E l ^{n 1 —} t¹^ • t² 2 n ₀

• ° 2

j = 1

Ряд Маклорена для данного выражения будет:

2 n 0 ^{2         j}

—

—¹ 1 ⁴ • ° 4 4 n 0 ⁴ • 2        ^j

- -

1 k 2 k 2 n ₀ ² k

t 2 k

2 k

—

Имеем сумму n0 рядов. Погрешность (остаточный член) каждого ряда будем оценивать в форме Коши, т. е.

₍ , xk ^{+ 1} (1 — ^ ) k

0 <  ^ <  1.

r ( x ) =-- k +1(1 — ^x)k+1

В знаменателе стоит разность, т. к. рассматриваем in (1 — x ).

Для каждого ряда суммы имеем:

22 t ° , 2 n 0 ²

k

------- <  1, т. к. £ x <  £ ;

1 — £ x

< n ₀, т. к. n ₀ >  2 и 1 >  £ x .

x ^k + 1

Поэтому r ( x ) < -—- • n 0 , т. е.

n 0       t ^{2 k} + ² • _a ^{2 k} + ²

R ^{x (} t ^l^ ^{k + 1} • n ₀ ^{2 k + 1} •( k + 1 )"

Потребуем в записанном неравенстве для k = 1 выполнения условия:

A t 4 • a 4 ^s

= 8 n 03 "2,                      ¹

где s — сколь угодно малое положительное число.

Так как t <  3 • a max , то, усилив неравенство (5), получим:

^{3   a} max

8 n 0 ²

s

< —

.

Отсюда:

4,5 • a max

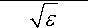
+ 1.

Можно было бы, заменив t на 3 a max в (5), использовать рекуррентный метод. Полагаем сначала n ₀ = 2 и проверяем выполнение неравенства (5) для двух законов распределения при заданных средних квадратических отклонениях a 1 и a ₂ .Если оно выполняется, то завершаем рекуррентный процесс. В противном случае полагаем n ₀ = n ₀ + 1 и снова проверяем выполнение неравенства (5) для трех законов распределения при заданных a ₁ , a ₂ и a ₃ и т. д.

Из (4) и (6) находим

+ 4- (7)

n >  n ₀ = max <

+ 2,

4,5 • a max

s

n ₀

, 2 _2                     S

• t • a, с точностью —. j 2

Таким образом, ln q_x ( t ) = — = — 2—

' = 1 ^{2 n} 0

Положим n0

12 a = — a : a'.

ⁿ 0 v ' = 1

Тогда a t

—

n 0

— ^S = Z A t "a a , 2 '" = 1 2 n 0 ² '

—

n ₀

— <  l nq_x ( t ) <— У — t - t ^a 2 2 x^A) 4 = 1 2 n 0 ² '

S      12 2 S

+ - = —a ² 1 ² + -. (8)

2    2       2

Получаем

qx(t)

n ₀

E ¹ ,2 ^2 t a 2 j 2 n ₀

e ' = 1

—t a

= e

¹ t ²

2/ a ^г

.

Используя дифференциал, оценим погрешность определения функции q x ( t ) . А именно:

n

qx (t)- e

2 n 0²

e

n ₀

Z ¹ ,2 ^2

2 n о²    j ^{8    8}

"      — < —.

Очевидно, относительная погрешность также будет меньше 8 . Из определения характеристической функции имеем:

да qx (t )= J eixt • f (x) dx.

-да

Тогда плотность распределения вероятностей i да f (x ) = — Je" itxqx (t)dt.

2 n

С

учетом

да

1 ‘

-да

Ax ² ± 2 Bx - C

формулы, AC - B ²

-да приведенной

в

книге

[5],

e ^A , формул (8)–(10) получаем

При о >  0,399 -Д- • e - V 2 по

) = —¹ e 2о ² f 1 -

) 72 Ло ^e I ¹

x ²

^{2 о 2} <  1. Поэтому с

8

8

точностью

1        -

,— • e ^{2 о}

2по

.

Очевидно, относительная погрешность не

превосходит

8

. Путем со-

ответствующего масштабирования ограничения на о можно снять.

Значит, x имеет нормальное распределение с m x = 0, o x = о .

Заметим, что при вычислении f ( x ) используется несобственный интеграл при t е ( -да , да ). А именно:

1 x

1   -? ^2

= — e ^{2 о}

2 п

да

1 Г   - itx eitx

2 n

-да

2п

о

- ¹ 1 2 о ²

• e ²

да dt = — [ e 2 n J

-да

¹ t ² о ² + itx 2

1 да

-да

- 1 о 2

dt =

e

2по

2 о о

.

Однако t е [ - 3 о max , 3 o _max ]. Покажем, что с любой заданной точностью

8

— при соответствующем n0 интеграл (12) в пределах от 3оmax до да бу- дет сколь угодно мало отличаться от —. Положим u = -° t + -ix- , тогда 4               V2 V

, О , О .^ ) du = —^dt . Пусть b =     3 о _яv + —г .

1max 2

V2             V2 V о )

to — 102It+^У1

Имеем: j e 2 V О ) dt =~7=je u du. 30max

Для вычисления последнего интеграла возведем его в квадрат, затем перейдем к двойному интегралу в полярных координатах:

to j e-udu

V b to

О Г — u-

to

to

П to

= j e u du - J e v dv = j d ^- j re ^r dr , где r ² = u ² + v ² , т. е.

b ₁

b ₁

ПО ^{— 1} b l I²

--e ²

< — . Отсюда l b ,|² >- 2in — ^—

4              ^{1 11}           2 х П

Поскольку x >  m - 9 o max венство, получим:

с вероятностью 0,99, то, усилив последнее нера-

^{4,5 0} min

■ max + 45,5 n 2 + 2 n _oln /? n

2 V ^ПО max

где ° min = min ^o

j = 1, n 0 , т. е.

22,75 n 2 + n o (ln — + jin n o — 1,264 — In о _) + 2,25 o min - о m^ >  0. (13)

Из этого неравенства при заданных — , о _min и о _max находится соответствующее значение n ₀ .

Поскольку n ₀ >  -^-in n ₀, то последнее неравенство можно усилить так:

21,75 n ₀ >- in — + 1,264 - in о _х , т. е.

0max

7 +1,264 + in оах nn > т. к. минимальное — будем рассматривать равным 0,001. Отсюда n 0 > 0,41 + in О max.

Это более простая, но более грубая оценка, чем получаемая из неравенства (13).

Аналогично рассматривается интеграл от -to до - 3 о _max.

^{3 o} max

Следовательно, f ( x ) = j e

^{3 o} max

—1

—

' qx (t)dt с точностью 2 приn- удов- летворяющем (14).

Таким образом, с точностью £ средняя арифметическая количества n >  n 0 суммируемых независимых случайных величин с одинаковыми математическими ожиданиями и разными дисперсиями при выполнении условия

4,5 a max

n ₀ = max <

£

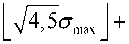
+ 1, |h a ma. + 0,41J> (15)

имеет нормальный закон распределения.

Теорема доказана .

2 Исследование зависимости числа слагаемых ЦПТ от точности

В таблице 1 для заданного значения £ приведены соответствующие значения n ₀ для a _max = 1.

Зависимость n ₀ от £               Таблица 1

£	0,001	0,002	0,0028	0,003	0,004	0,005	0,01	0,1	0,5	0,9
n 0	102	72	61	59	51	46	33	11	6	6

Зависимость числа слагаемых n ₀ от точности £ графически изображена на рис. 1.

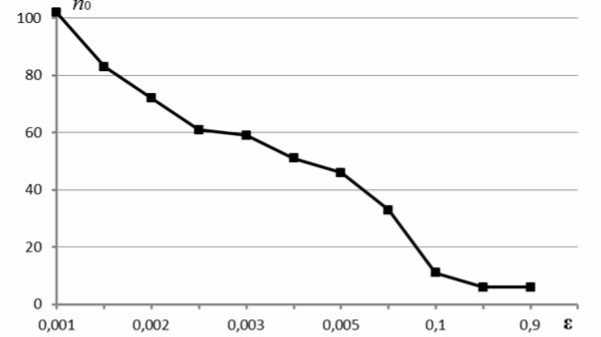
Рис. 1. Зависимость n ₀ от £

С помощью средства MS Excel «Линия тренда» эту зависимость можно аппроксимировать полиномом шестой степени (коэффициент детерминации R ² = 0,9959 ):

n 0 =^- 0,0013 £ ⁶ + 0,0587 £ ⁵ - 0,9298 £ ⁴ + б,4444 £ ³ - 18,65б £ ² + 5,5б39 £ + 109,25 j .

Следствие из теоремы. При числе слагаемых n >  n ₀ ( n ₀ удовлетворяет равенству (14)) сумма n независимых случайных величин (с одинаковыми математическими ожиданиями и дисперсиями, ограниченными 32

сверху значением о max ) имеет нормальный закон распределения вероятностей.

При значениях n >  n 0 величина X имеет нормальное распределение, поэтому Y = nX будет иметь нормальное распределение (при тех же значениях n ).

Заключение

На основе доказанной теоремы и ее следствия выведены условия, определяющие количество слагаемых, для которого средняя выборочная и сумма слагаемых (в ЦПТ) имеют нормальный закон распределения (с заданной точностью). Исследована зависимость числа слагаемых ЦПТ от заданной точности и дисперсии выборки.