Оценка напряженно деформированного состояния вязкоупругой крупногабаритной оболочечной конструкции, нагруженной внутренним давлением

В настоящее время имеются проекты создания крупногабаритных конструкций из армированных пластиков для освоения Космического пространства [1]. Материалом такой конструкции может служить композит, состоящий из углеродной ткани и эпоксидной матрицы [2]. Такой материал проявляет вязкоупругие свойства, поэтому актуальным является исследование поведения таких конструкций во времени под действием различных нагрузок. В настоящей работе проводится оценка напряженно-деформированного состояния вязкоупругой крупногабаритной оболочечной конструкции, нагруженной внутренним давлением.

Постановка задачи. Рассматривается оболочечная конструкция под действием внутреннего давления в одну атмосферу. Оболочка состоит из основной цилиндрической части и двух полусфер, геометрические размеры конструкции показаны на рис.1.

Работа выполнена при поддержке гранта РФФИ №12-08-00970-а.

Материал конструкции – ортогонально армированный углепластик с объемным содержанием волокна 0,6. В качестве связующего служит эпоксидная смола ЭДТ–10. Приведенные вязко упругие свойства углепластика рассчитываются в два этапа: эффективные свойства однонаправленого армированного материала рассчитывались в пространстве изображений по Лапласу – Карсону методом условных моментных функций; расчет приведенных свойств слоистого пакета проводился осреднением по толщине. Переход к начальным функциям осуществлялся методом нелинейной аппроксимации [3]. В частности, для ортогонально армированного в плоскости x₂ х₃ под углами ± п /4 относительно оси x углепластика функции релаксации представляются в виде

R j ( t ) = C i + t C j ) e - ^Y ( k ) ^t , k = 1 (1)

[ C j) ] = МПа, Y^(k ) ] = c -1 .

Параметры, входящие в формулу (1), представлены в таблице. Задача о нагружении оболочки рассматривается в двух вариантах. В первом варианте углеродные волокна параллельны образующим оболочки и ее меридианам. Во втором варианте углы составляют (+45о, –45о) с образующими оболочки. Рассматриваемый материал является термореологически простым и имеет ядра ползучести ограниченного типа. Это позволяет провести оценку вязкоупругого поведения конструкции путем решения упругих задач с динамическими и равновесными модулями.

а

Рис. 1. Внешний вид конструкции а) и схема б). Толщина оболочки 0,01 м

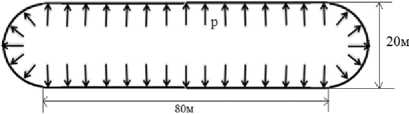
б

Параметры матрицы функций релаксации

k	γ ( k )	( k ) C 11	( k )         ( k ) C 12 = C 13	( k )          ( k ) C 22 = C 33	( k ) C 23	( k ) C 44	( k )          ( k ) C 55 = C 66
	–	4773	2505	39720	35279	34980	1509
1	0.2072 10-1	74.24	-30.81	345.0	-311.1	36.14	105.1
2	0.4570 10-1	57.97	-24.02	240.5	-243.5	28.04	82.69
3	0.8747 10-1	162.2	-67.02	721.3	-648.2	76.87	227.7
4	0.5193 10-1	397.2	-162.6	1801	-1614	183.9	573.6
5	0.6165 10-1	527.0	-208.8	1621	-1372	200.3	719.5

б

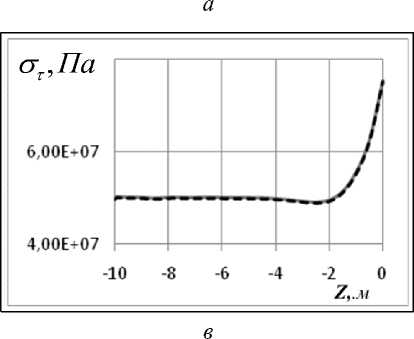
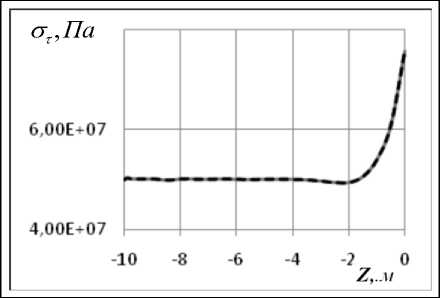
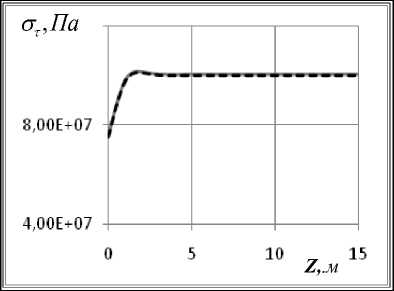
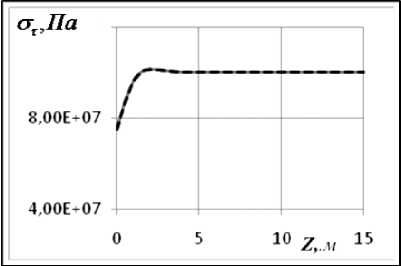
Рис. 2. Графики зависимости от координаты Z окружных а), в) на сферической части; б), г) – на цилиндрической; графики а), б) для длительных модулей упругости, в) и г) – для динамических

г

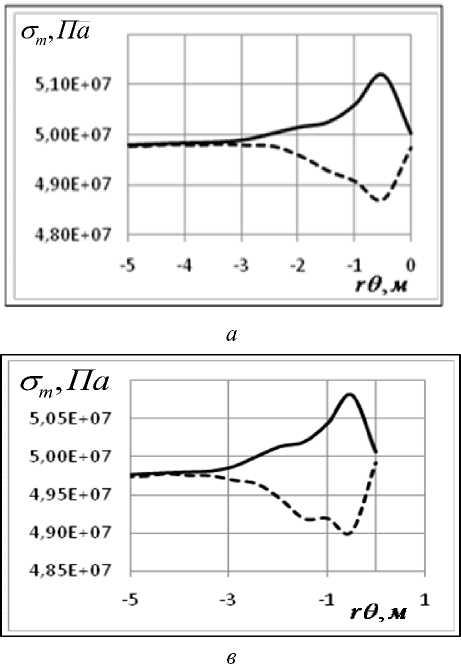
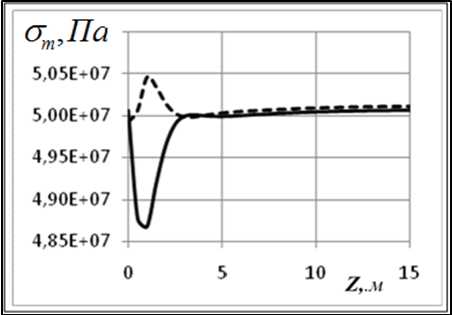
Рис. 3. Напряжения σ ( r θ ) для сферической а), в) и σ ( z ) для цилиндрической части б), г); графики а), б) для длительных модулей упругости, в) и г) – для динамических

В квазистационарном процессе вязко упругое решение задачи будет ограничено этими двумя решениями. Задача решается с использованием инженерного пакета ANSYS в трехмерной постановке.

Результаты вычислений. Наибольший интерес представляет распределение напряжений в области стыка цилиндрической и сферической частей конструкции, в которой возникает концентрация напряжений (краевой эффект). На рис. 2, 3 представлены мериди-альные ( σ ) и окружные ( σ_τ ) напряжения для варианта 1. Сплошной линией показаны напряжения на внутренней поверхности оболочки, штриховой – на внешней.

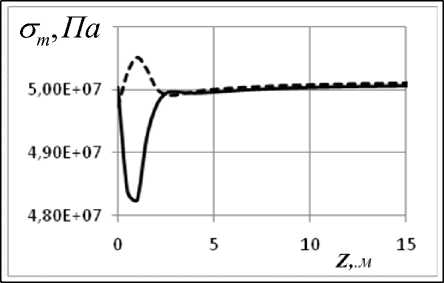
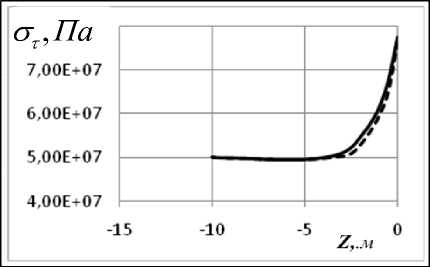
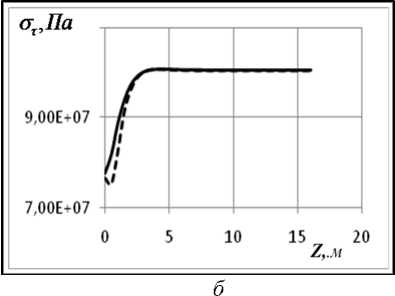
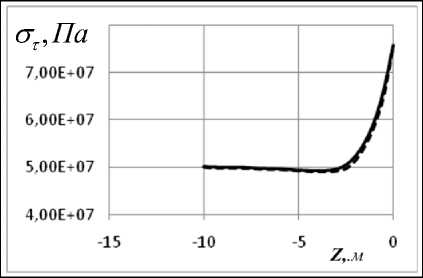
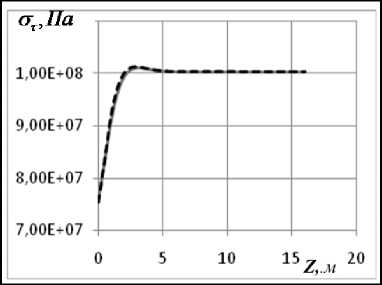
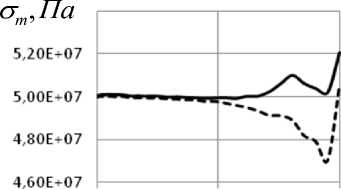
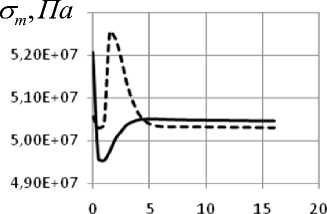
На рис. 4, 5 представлены мериди-альные ( σ _m ) и окружные ( σ_τ ) напряжения для варианта 2.

Как видно из графиков, в зоне стыка цилиндрической и сферической частей возникает концентрация напряжений. Эта область занимает примерно по 5 м от границы стыка в обе стороны. Величина коэффициента концентрации составляет 5–7 %. При сравнении результатов, полученных для длительных и динамических модулей, обна-руживаем небольшое увеличение меридиальных напряжений с течением времени.

Проведенный численный анализ сравним с аналитическим решением, полученным с использованием методов расчета И.А. Биргера и C.П. Тимошенко [4, 5] на основе гипотезы плоских сечений.

Напряжения вне зоны краевого эффекта не зависят от варианта расположения слоев.

Для цилиндрической части

σ = pR =108Па, τh

σ = ^pR = 5 ⋅ 10⁷ Па .

m

Для сферической части

σ = σ = ^p = 5 ⋅ 10⁷ Па .

τ    m

В окрестности сопряжения сферической и цилиндрической частей возникает резкое изменение напряжений (т.н. краевой эффект). Максимальные напряжения в зоне краевого эффекта по теории Тимошенко [5]:

K ₁₁ C ₂₂ - 2 K ₁₂ K ₂₁ C ₁₂ + K ₂₂ C ₁₁

11               _Ω

;

C = hB ;К =—В ■ ij                ij ; ij                     ij ;

σ = 1.293 pR ≈ 6.46 ⋅ 10⁸ Па .

m        _{2 h}

^B 11

Окружные напряжения в среднем на 30 % больше меридиальных:

E ₁            E ₂

; B ₂₂ =          ;

1 -νν      1 -νν

B 12

σ = 1.032 ^pR ≈ 2 ⋅ 10⁹ Па . τ _h

ν ₁ E ₁      ν ₂ E ₂

1 - νν   1 - νν ^.

Рассчитаем зону распространения краевого эффекта s*[4]:

*       ^{2 R}

s =πу — ; Δ=

Ω

; Ω = C C - C ²;

В результате расчета получаем, что s ^* ≈ 2.78 м для варианта 1 и s ^* ≈ 4.7 м для варианта 2, что вполне согласуется с решением в ANSYS, поэтому оценочные расчеты о поведении рассматриваемой конструкции можно проводить, используя аналитические зависимости.

^ ^C 11 ^D 1

в                                                     г

Рис. 4 . Графики зависимости от координаты Z окружных а), в) на сферической части; б), г) – на цилиндрической; графики а), б) для длительных модулей упругости, в) и г) – для динамических

Выводы

• •    Исследования крупногабаритных оболочечных конструкций из армированных углепластиков для случаев, рассмотренных в данной статье симметричных ортогональных пакетов, с целью оценки влияния вязко упругих свойств материала можно

проводить по его динамическим и равновесным константам.

• •    Оценочные расчеты о поведении рассматриваемой конструкции можно проводить, используя аналитические зависимости.

  
  
  
  

  Z,..u

  
  
  

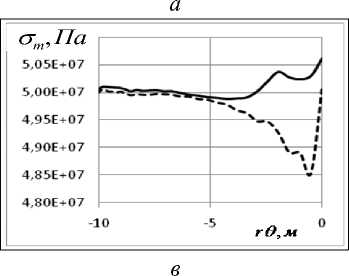
  Рис. 5. Напряжения σ ( r θ ) для сферической части а), в) и σ ( z ) для цилиндрической б), г); графики а), б) для длительных модулей упругости, в) и г) – для динамических

  
  

  б

  

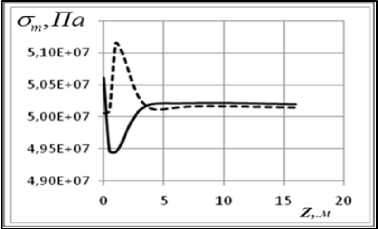
  г