Оценка параметров интерферограмм, необходимых для определения радиуса кривизны в вершине лежащей капли

Метод «лежащей» капли широко применяется для определения поверхностного натяжения агрессивных жидкостей, таких как высокотемпературные металлические расплавы [1]. Для этого используются геометрические параметры капли, оцениваемые по ее фотографическому или цифровому изображению. Обычно в качестве таких параметров берутся размер экватора капли и расстояние от него до ее вершины. Определение положения экватора капли затруднительно из-за того, что в районе экватора радиус капли слабо зависит от расстояния до вершины, что обуславливает погрешности в определении этого расстояния и как следствие - погрешности в определении величины поверхностного натяжения. Кроме того, требование наличия у капли экватора сужает возможность экспериментировать с разными жидкостями, помещенными на различные подложки. Поэтому представляет интерес рассмотреть другой набор геометрических параметров капли, который можно было бы использовать для решения той же задачи с большей точностью.

В работе [2] нами был предложен способ наблюдения за формой капли в окрестности ее вершины, отличающийся высокой пространственной чувствительностью и безинерционностью. Здесь вершина капли участвует в формировании интерференционной картины, параметры которой существенно зависят от радиуса ее кривизны. Расшифровка цифровой копии интерферограммы имеет, однако, свои трудности, связанные с присутствием на ней кроме полезной информации также и разного рода случайных возмущений, например, спекл-шума, шума, вызванного дифракцией света на пылинках, лежащих на поверхности элементов оптической схемы, и т.п. Это ставит вопрос о разработке таких методов оценки параметров интерференционной картины, необходимых для реализации метода [2], которые были бы устойчивы по отношению к этим возмущениям и обеспечивали бы достаточную точность результатов. В настоящем сообщении описывается несколько подходов к обработке зашумленных интерферограмм. Рассмотрены также некоторые аспекты повышения точности определения радиуса кривизны в вершине капли за счет изменения оптической схемы и методики эксперимента [2].

Эксперимент

Лежащая капля жидкости является оптическим объектом с фазовой отражающей поверхностью. Поставим задачу определить радиус кривизны К в вершине испаряющейся лежащей капли в любой момент времени в процессе ее испарения. Знание этого радиуса позволит совместно с численным решением уравнения Лапласа и нахождением одной из координат профиля капли определить величину силы поверхностного натяжения жидкости капли.

Неразведенный вертикальный луч лазера, отразившись от вершины осесимметричной лежащей (или висящей) капли, трансформируется в сферическое волновое поле, поскольку в окрестности вершины поверхность капли является сферической. Это волновое поле можно представить как поле, сформированное точечным источником света, расположенным на расстоянии К/2 за по- верхностью вершины капли. Если это волновое поле наложить на когерентное ему плоское волновое поле, возникнет интерференционная картина, несущая информацию о радиусе кривизны капли. Схема данного эксперимента, подробно рассмотренного в работе [2], приведена на рис. 1. Здесь Н- расстояние от подложки, на которой лежит капля, до фокальной плоскости объектива, В - расстояние от фокальной плоскости объектива до ПЗС матрицы, которая регистрирует интерферограмму, h - высота капли,/- длина фокусного расстояния объектива. Отметим, что линза, отражением от поверхности которой создается опорное поле, таким образом позиционирована по отношению к объективу, что формирует на ПЗС матрице плоское волновое поле.

На рис. 2. приведена расчетная схема эксперимента, позволяющего на основе известных соотношений интерферометрии и геометрической оптики выразить величину R через метрические параметры оптической схемы.

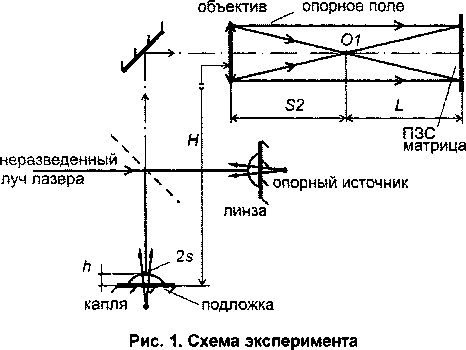
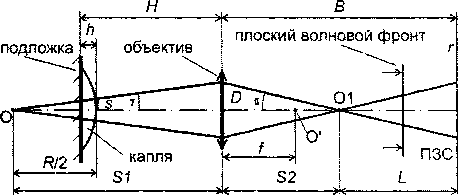
Рис. 2. Расчетная схема

Анализ расчетной схемы приводит к следующему выражению для R через геометрические параметры установки:

R=-— + 2А-2Я.                    (1)

Величины Н и В в (1) необходимо найти экспериментально. Покажем, как это можно сделать.

Если на подложку вместо капли поочередно установить две плоско-выпуклые линзы с известными радиусами кривизны ^ и J?2 и толщинами ^ и /^, для которых расстояния от пере тяжки Ох до места расположения ПЗС матрицы будут равны L, и Д тогда применение соотно шения (1) для каждого из этих расположений приводит к следующей системе уравнений для определения неизвестных ВиН:

Г 2

R_x=-— + 2/?₁-2Я

R^ =  —— + 2/^ - 2Я ~f~ В-Ц

Таким образом, задача сводится к нахождению значений L, / и Ь₂ . Для этого вновь обратимся к рис. 2. Можно видеть, что в плоскости ПЗС-матрицы интерферируют два волновых поля: плоское волновое поле, сформированное опорным источником (рис. 1), и сферическое волновое поле, сформированное точечным источником, расположенным в точке О_х . Картина интерференции представляет собой систему чередующихся светлых и темных колец (колец Ньютона). Пусть г - расстояние от центра интерферограммы до точки наблюдения в плоскости ПЗС матрицы. В случае, когда в центре интерферограммы ( г = 0) оптическая разность хода А_о плоского и сферического волновых фронтов равна нулю, можно записать

\ = r²/2L,                                    (3)

где А - оптическая разность хода в точке наблюдения.

Для светлых колец на интерферограмме можно записать А = N • X , где N - номер кольца, X - длина волны лазера. Тогда из равенства (3) получим

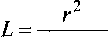
Таким образом, определив по интерферограмме радиусы светлых колец, можно найти искомый параметр L . Аналогичным образом можно получить значение L , используя темные кольца, для которых А = (2 • А -1)^, где А = 1,2,3, ...

В экспериментах использовался объектив «Индустар-37» с фокусным расстоянием/= 300 мм и лазер ЛГН-215 с длиной волны X = 0,6328 мкм. Размер ПЗС-матрицы составлял 6,7 х 5,0 мм, параметры Н и В были около 360 и 3100 мм соответственно. Для этих условий оценка размера 2s области около вершины капли, участвующей в формировании картины интерференции (см. рис. 1, 2), дает 2s ~ 150 т- 300 мкм. Это оправдывает высказанное выше предположение о сферичности поверхности капли вблизи ее вершины. Более подробно с проведением экспериментов можно ознакомиться в работе [2].

Параметры интерферограммы

Метод определения L, основанный на измерении радиуса колец и использовании соотношения (4), использовался нами ранее в экспериментах [2]. Однако, наблюдаемые на опыте интерферограммы (см. ниже рис. 3) имеют такой вид, что вопрос о том, как определять радиус кольца, не является праздным. При выбранном способе регистрации (ПЗС-матрица) этот вопрос, очевидно, останется даже в отсутствие обсуждавшихся выше шумов - как следствие дискретизации поля изображения и интенсивности света в каждой точке этого поля (пикселе). Поэтому оценка параметров картины интерференции (например, радиусов колец) вряд ли может быть сделана с высокой точностью, если опираться на какой-либо локальный метод обработки, оперирующий лишь с отдельными элементами картины. Более целесообразными представляются глобальные способы обработки, оперирующие со всей информацией, представленной на цифровом образе интерферограммы. Ниже описываются методы, использованные нами.

Для обработки интеферограммы необходимо оценить положение ее геометрического центра. По аналогии с методом определения центра масс тела в механике с использованием статических моментов инерции будем рассматривать интерферограмму как совокупность точек, имеющих «массу», пропорциональную их интенсивности. Тогда положение X_C,Y_C центра (инерции) интерферограммы можно определить как

N М            N М

XX^ХМXX )

----■ Yc=A4ng----■<»

* ji J где xt p y, j есть координаты пикселя (z,j) цифровой копии интерферограммы, Ip - значение этого пикселя (интенсивность света в месте его расположения). После этого можно рассмотреть некоторый луч, исходящий из центра интерферограммы, и построить распределение интенсивности света вдоль этого луча. Затем это распределение следует усреднить по направлениям всевозможных лучей, исходящих из центра и определить места (расстояния до центра), где интенсивность достигает максимумов (минимумов). Эти расстояния будут радиусами светлых (темных) колец, необходимыми для определения L с использованием формулы (4). Оказалось, однако, что хотя такой метод и работоспособен, но не слишком устойчив из-за того, что световой поток, приходящий на эквивалентные друг другу участки интерферограммы (то есть, находящиеся в одинаковом положении по отношению к ее центру), различен. Причин для этого может быть несколько, какая из них играет роль в данном случае — пока не ясно. Понятно только, что при неравномерном распределении «фона» по ПЗС матрице положение центра интерференционной картины, определяемое по (5), будет зависеть от вида этого (неконтролируемого) распределения.

Второй подход к решению задачи определения радиусов колец состоял в том, что предварительно задавалась система концентрических окружностей с центром, примерно соответствующим центру интерферограммы, и радиусами, разность квадратов величин которых была постоянна для соседних окружностей. Определялась и суммировалась интенсивность света экспериментальной интерферограммы во всех точках этих окружностей. Затем с использованием метода Нелдера-Мида [3] выполнялся поиск таких радиусов окружностей и положения их центра, которые обеспечивают минимальное значение этой суммарной интенсивности, если разыскиваются радиусы темных колец, и максимальную суммарную интенсивность - для светлых колец. При апробации этого подхода на практике оказалось, что он также ведет к не вполне устойчивым результатам из-за большой пологости оптимизируемой целевой функции в области разыскиваемых экстремумов.

Анализ полученных результатов привел нас к выводу, что желательно использовать данные о распределении интенсивности света, предоставляемые всем полем интерферограммы. С целью определения ее параметров предлагается составить и минимизировать целевую функцию Z, представляющую собой уклонение расчетной ( 1^ ) интенсивности света, вычисленной с использованием математической модели интерференции, от интенсивности, наблюдаемой в эксперименте

* j где / и у - координаты пикселей на цифровом изображении интерферограммы. Математическая модель опирается на законы интерференции плоского и сферического когерентных волновых полей, учитывает положение центра (ХС,УС) интерферограммы, ее среднюю (/0) и минимальную

(А/) интенсивности, разницу фаз ф₀ плоского и сферического волновых полей в центре интерферограммы:

= ((То - Л/) • (1 + cos^'⁽⁰ ~                  ₊ ^_{о)) +} а/) . e^-r             ₍₇₎

л-L

Экспоненциальный множитель с показателем А описывает, если необходимо, уменьшение интенсивности от центра к краям интерферограммы. Заметим, что в предлагаемом подходе нет нужды определять радиусы колец непосредственно: искомый параметр L оптической схемы находится в процессе минимизации (6), осуществляемом методом Нелдера-Мида [3], как и выше.

Метод (6), (7) был реализован в виде программы с графическим интерфейсом. На рис. 3 в качестве примера приведена экранная копия рабочего окна этой программы. Слева приведено цифровое изображение интерферограммы, наблюдаемой в эксперименте, справа - результат его обработки с использованием модели (7). Для проверки работоспособности метода были выполнены эксперименты, в которых на место исследуемой капли ставились линзы с известными радиусами кривизны R_3majlOH (эталонные). Результаты (7?_экс„) оценки этих радиусов описанным методом, включающим определение параметра L с помощью (6) и (7), приведены в таблице. Погрешность в определении R_3KCn соответствует доверительной вероятности 95 %. Выполненные расчеты показали, что в отношении искомого параметра L предложенная методика дает устойчивые результаты: разброс L при повторении опытов составляет около 0,1 % при L — 1000 мм и около 0,06 % при £-1400 мм.         _____________________________

№ опыта	^эксп ’ ^™	R    мм эталон ’ 1
1	20,66 ±0,34	20,7
2	7,88 ±0,28	7,85

Заметим, что теперь достижимая точность определения £ более чем порядок превосходит погрешность определения непосредственно интересующей нас величины R3Kcn. Это связано с тем, что необходимые для расчета R3KCn параметры Ни В оптической схемы находятся из систе мы (2), содержащей радиусы кривизны Rx 2 эталонных линз, которые также имеют некоторую погрешность. Поэтому для повышения точности экспериментов необходимо либо предпринять специальные меры для уменьшения этой погрешности, либо найти другой, более точный способ определения обоих параметров Н и В или хотя бы одного из них. Укажем один из возможных

Рис. 3. Рабочее окно программы, реализующей метод (6)—(7) оценки параметров интерферограммы

Если вместо капли на подложку (см. рис. 1) установить плоскопараллельную пластинку, то после отражения от нее луча лазера волновое поле останется плоским. Пройдя через объектив, это поле трансформируется в сферическое и сойдется в точке О' - фокусе объектива (см. рис. 4 с эквивалентной схемой). Тогда

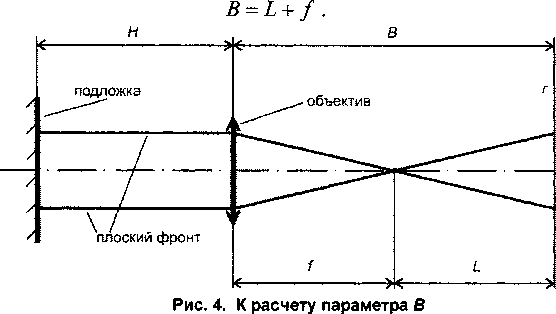
Таким образом, чтобы найти В, достаточно определить L, что можно сделать одним из методов, описанных только что. Второй неизвестный параметр, Н , приходится, к сожалению, определять с помощью эталонной линзы:

Н=_х *, +h                          (9)

• 7 в-Е

С использованием этого метода радиус кривизны эталонной линзы, использованной в тестовом опыте 1 (см. таблицу), теперь оценивается как 20,7 ±0,10 мм.

Заключение

С целью определения параметров, необходимых для расчета радиуса кривизны в вершине лежащей капли предложенным ранее методом [2], рассмотрены локальные и глобальные методы обработки цифровых копий интерферограмм, возмущенных шумами различного происхождения. Показано, что локальные методы, основанные на анализе отдельных элементов интерференционной картины (темных или светлых колец), менее устойчивы к возмущениям, чем глобальный метод, учитывающий распределение интенсивности на картине интерференции в целом. Предложены некоторые изменения в методике выполнения экспериментов, ведущие к повышению их точности.

Работа выполнена при поддержке РФФИ, грант 10-03-00719-а.