Оценка погрешности вычисления площади при кусочно-полиномиальной аппроксимации

DOI:

При исследовании вопросов равномерной сходимости приближенных решений краевых задач для уравнений с частными производными одной из ключевых задач является задача определения погрешности аппроксимации уравнения и краевых условий. Если при этом используется вариационный метод, то требуется знать, с какой точностью аппроксимируется соответствующий функционал. Например, при решении задачи Дирихле для уравнения минимальной поверхности часто применяется вариационный метод, в котором ищется поверхность минимальной площади в классе кусочно-линейных поверхностей [3]. В этой работе для прямоугольной области было установлено, что площадь графика достаточно гладкой функции вычисляется с погрешностью порядка 0(h2), где h — максимальная сторона треугольников, на которые разбивается прямоугольник. Этот факт был применен авторами для доказательства сходимости кусочно-линейных решений равнения минимальной поверхности.

В настоящей работе мы изучаем вопрос о степени точности вычисления функционала площади достаточно гладкой функции при ее аппроксимации кусочно-полиномиальными функциями, заданными на произвольной треугольной сетке. Отметим, что при наличии краевых условий и некоторой модификации вариационного метода задача об оценке погрешности может быть сформулирована следующим образом. Пусть в многоугольной области Q С R 2 заданы достаточно гладкие функции / и р такие, что / | s q = p| d Q . Зафиксируем некоторое разбиение области Q на треугольники и через h обозначим максимальную сторону всех этих треугольников. Рассмотрим кусочно-полиномиальную функцию м, которая совпадает с / — р в узлах сетки. Требуется оценить разность площадей графиков функции / и р + м.

Отметим также, что в работах [1], [5] получены оценки погрешности вычисления площади поверхностей для триангуляции частного вида, построенной по прямоугольной сетке.

1. Основные результаты

Рассмотрим функционал, задаваемый интегралом

I (/) = Ц G(x,/, V /)d^ 2 , Ω

который определен для функций / G С ^m+ 1 (Q). Отметим, что уравнение Эйлера — Лагранжа вариационной задачи для этого функционала имеет вид:

п

Q[/ ] = E (G' _t . U, /, V /)G — G y (ж, /, V /) = 0.                 (2)

Если подынтегральное выражение G(x, /, V /) равно ^/1 + |V / 1 ² , уравнением (2) является уравнение минимальной поверхности

у to■"

/ х _г

VTTiW

) 0

Пусть задана многоугольная ограниченная область Q С R ² . Рассмотрим разбиение этого многоугольника на треугольники. Т 1 ,Т 2 ,...,T n . И пусть М 1 ,М 2 ,...,M _q — все вершины этих треугольников. Будем предполагать, что ни одна из точек М _г не является внутренней точкой ни одной из сторон треугольников. Через Г ₅ будем обозначать стороны всех треугольников, s = 1, 2, ...L, а максимальный диаметр всех треугольников обозначим через h, то есть h = max diamT k , где diamF = sup ( | ж — ^ | : х,у G F ), а _к — минимальный угол в треугольнике Т _к , а = min а _к > 0. к

Рис. 1. Триангуляция области Ω

Для построения кусочно-полиномиальной функции степени т нужно к имеющимся вершинам треугольников M 1 ,M 2 ,...,M _q добавить дополнительные точки следующим образом. Для произвольного треугольника Т _к , каждая сторона которого разбита на т — 1 равных частей, и через точки разбиения проведены прямые, параллельные сторонам треугольника. Стороны треугольников также будем относить к множеству этих прямых. Обозначим через А _к множество, состоящее из точек пересечения этих прямых, лежащих в замкнутом треугольнике Т к . Получаем набор точек А 1 , А 2 ,..., А, _г , который содержит и вершины всех треугольников Т _к . Далее зададим значения м 1 ,м ₂ ,../и _г и построим в каждом треугольнике многочлен степени т так, чтобы его значения в точках А _г совпадали бы с м _г . Получившуюся кусочно-полиномиальную функцию будем обозначать через м. Данная функция будет непрерывной в Q.

Нам далее понадобится оценка погрешности приближения производных функции производными интерполяционного многочлена. Пусть / Е Сm+1(Q) и Мг = / (Аг),г = = 1,...,г. В работе [6] доказывается, что для всех (х1,х2) Е Тк выполнено неравенство ds(/(^1 , Х2) — и(Х1,Х2))

Эх к ¹ 9x^ 2

< К (sin 0 ) ^s Mh ^{m s+1} , 0 <  s < т, к 1 + к ₂ = s, (3)

где θ — максимальный угол триангуляции,

Q m +l j 8x ^q1 8x' ^ ^{+q —}

\, q = 0,

., т + 1, и посто-

янная К не зависит от разбиения {Т _к } _к=1 , области Q и /.

Пусть ф Е С ^m+1 (Q), / \ s q = ф\ д Q и обозначим через м кусочно-полиномиальную функцию, построенную по значениям функции / — ф . Положим / ^р = ф + м и пусть д¹ = / ^р + £(/ — / ^р ). Для каждой стороны треугольников выберем нормаль v так, что для d Q она будет внешней. По аналогии с работами [2] и [4] доказывается следующее утверждение.

Теорема 1. Справедливо равенство

TV                 ¹                                   2       1

I(f ) — I(/ ^р ) = Е /(z — ^п ) j ^[д ¹ l-t-ж + j(z — и) Е V i I G [ . (ж,д¹, Vд ^t )dtdS + к -1

Т к

d Q

i -1

+

Е [ (z — .) ^Е vj внутр. r^{J r} t         г-1   0

G , _t (ж, д + , Vд ^t+ ) — G^ _t (ж, д!, V д - )dtdS,

где z = / — ф , д + ,д — — функция д¹, рассматриваемая в двух треугольниках с общей стороной Г , причем д + соответствует тому треугольнику, для которого нормаль ν является внешней.

Доказательство. Заметим, что

-                                    - Г 1 d

I(/ ) — I(/^р ) = ^Е J(GM, V /) — G(ж,/ ^р , V / ^р )) = ^ЕУ J - №,д ' , Чд*У)«аж =

т , 0

^dG       _х dG                 f f dG

’ aU^{(z — и)}ЕЕ di^{(z — и}М ^dжdt = J / aU^{(z — u)dжdt +}

L                   1=1 ^г            J            ^{к -}1 Т_к О

1 -      2

+   ЕЕ dG ( ^г— ”) ^ . -ж-t.

0 ^к -1 Т , < -1

Рассмотрим отдельно интеграл

у И^{(z —и)} ^ ^-ж

Т к

Распишем его, воспользовавшись формулой Гаусса — Остроградского

У Ц^(z -о =

Т к

— / дж (110(ж,д * (ж), Vд ^t (ж))^ (z — и)-ж + j |^Е (z — u)v i ds.

Т к

8Т _к

Тогда

N            / 1            1                                   \

I(/ ) — I(/ ^р ) = Е /(z — и) ^У дUdжdt — / д 1 (дж (ж,д * (ж), Vд ^t (ж))) dжdt ) +

N                  2 Г г^С"¹

+ Е /(z — и) Е Ч d^dtds. к=1дТ к          i = 1   О ^

Распишем отдельно интеграл по границе

+

N              2     1

£ Л=-и) £ v ./ ^t = ¹ ₈ T .          ⁱ = ¹

9G

-— atas

9 t .

£  /(.-u) £ v.  ( внутр.Г rs         .=1   0

= /r - ^u) £/

d Q

9G, t d^ (x,++, Vy+)

-

dG„, .

-—atas + d t

dG ,  . „.Л

— ^(x,g_ , ^V g_ ) 9 t .             /

dtds,

где g + ,g -_ — функции g * , рассматриваемые в треугольниках с общей гранью Г ^ , причем g + соответствует тому треугольнику, для которого нормаль v является внешней.

Таким образом, окончательно приходим к равенству

N               1                 .           2

I (f) - I (fР ) = £ /А -и) / Q[g* ]dtdx + f(z -и) £ v. / Gt. (x,g*, Vg* )dtdS + k=1Tk         0               SQ         i=1

+

£ I ^{- - и)} £ ^v .   ^G t . ^(x, g + , ^Vg *+ )

-G ^ . (x,g t , Vg - )dtdS.

внутр.Г Г        i=10

Применим доказанное равенство для оценки погрешности вычисления графика функции

I(f ) = jj V ¹ + f « + fl > dx i dx 2

в случае плоской области Q С R ² . Пусть f Е С ^m+1 (Q). Положим М [ = max max lf _x. (x) | ,

¹      1 < i < 2 Q

М 2 =

max max l f _x._x. (x) | . Получим оценку 1 Q        ³

Q[ g‘\ = £ ( Gs . (x,g*, Vg * ))., - G , (x,g‘, Vg * ). i=1

Ясно, что

G , (x,g\ V g * ) = 0, так как G зависит только от V g * . Тогда

9G =      g . .

a t i.     V 1 + |V g * | ² ,

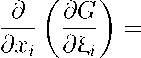
g . . . . • V 1 + |V » * | 2 - g . .

1 + |V g * | ²

g . . . . •⁽¹ + ^|V g * ^{| 2 ) -} g . . E g . j • g . , . j j=1

(1 + |V g * | ² ) ²

В силу того, что gxi = fP + t(fxi — f ^ ) = Tx. + "x. + t( f Xi — Tx. — ^Xj )

из неравенства (3) следует, что

^|g X _i I = |V x i ⁺ ^ X j + t^ Xi ^— V x i ^— ^ Xi ) ^|<

< M * + 2M / ^{- ф} + К (sin Q ) ^{- 1} Mh ^m = M 1 .

Аналогично

W_{Xi X j} I <  м ^ф + 2м / ^{- ф} + к (sin e ) ^-2 Mh ^m- 1 = M 2 .

Таким образом,

V ((1 + |V g ^x | 2V — у * -Ух Х

W] < У У^х • ----      ³  3    ³  <

Z_=1             (1 + |_W|2 ) 2     ) -

< E I » X , X 3 1 • ( (1 + |V g ^x | ² ) + | g X , X3 | ) <  4M 2 (1 + 2M 1 + M²) = 4M 2 (1 + 3M 2 ).

4,3 = 1

Далее ясно, что

E v ./

4 =1     00

у * dt

^2_1

V (1 + IWI ² )

≤ |ν| ·

Vg ^x

V (1 + |V y ^x | ² )

< 1 .

Зафиксируем внутреннее ребро Г5. Обозначим через Т+ и Т- треугольники, соприкасающиеся по этому ребру. Тогда на Г выполнено Vg+ — Vg- = t(Vfp)|т+ — (V/p)|т-. Заме тим, что для произвольных векторов ^, n G R” выполнено неравенство

ξη

-

1+ ξ ²       1+ η 2

≤

< 2 |^ — n| Действительно,

ξη

-

V 1+I ²   V 1+ n

^ + n — n n

- vm2   \ 1 ■ г/

≤

ξ-η

V T+I 2

^{+ |n|}( I vt+1? ^— vr+i? I )•

Оценим отдельно второе слагаемое

^|n| ( У 1+ С 2

V 1 + n ²

\ =    ( V T+ n — V 1+ C 2 A

)   ^{1 nl} \ V т+"^; n²V 1+ C 2 )

^Hn ^{2 —} ^ ^{2 |}                <       ^|n^|1^^— nHn + ^^|      <  ^^— n¹

(V1+I 2 + Vт+^;^) • VWV+V " (InI + |^|)Vт+^;n 2 V+V " V1+C 2 ^.

Тогда

ξη

--.     = — --.     =

VтП ² VW

≤

ξ -η

V1+I 2

+

VW

< 2 |^ — n| .

Поэтому

Vg ⁺            V g -

< 2 \V g + - g - \ = 2 \ ( V / ^p ) \ _T + - ( V / ^p ) | _T — | .

-

Vr+w;v  0 + \v g - \ 2

Теперь воспользуемся соотношением (3) для оценки модуля разности градиентов / и / ^р \V / - V/ ^p | <  К (sin 0 ) -1 Mh ^m .

Тогда

∑︁ 2

i=1 \

V ■ + k

V i + |V g + 1 ²

-

V g ⁺

V 1 + |V g - 1 ²

)

< 4К(sin 0 ) -1 Mh ^m .

Положим 4К(sin 0 ) ¹ M = C 1 . Теперь применим все доказанные выше неравенства к равенству (4), получим

II(/Р) — I(/)l< max Z -u\ l4M2(1+ M 1)\Q\ + \dQ| + C^m ^ |rs| у                              внутр.Г где |Q| — площадь фигуры Q, а |dQ| — ее периметр. Мы можем предположить, что триангуляция обладает таким свойством, что существует постоянная C2, которая не зависит от h и для которой выполнено h • ^2   \Г5\ < C2. Таким образом, мы пришли внутр.г к неравенству

• ^{11 (/ Р} ) ^{- 1 (/)|}< ^C 3 m a x ^|z -и\,

где

C 3 = ( 4M 2 (1 + M 1 ) \ Q \ + \ dQ \ +CiC2h^m-^ .

Далее несложно убедиться, что из оценки (3) следует, что \z — u \ <  KMh^{m +} . Таким образом, окончательно приходим к следующей оценке

\I(/ ^Р ) - I (/) \< C 3 KMh ^m+1 .

Заключение

В данной работе рассматривался вопрос об оценке точности кусочно-полиномиальной аппроксимации функционала площади C ^m+1 -гладкой поверхности. В результате была получена оценка степени приближения \I(/ ^р ) - I (/) \ <  C ₃ MKh ^m+1 .