Оценка работоспособности новых рабочих органов оболочечного типа для очистки и измельчения пищевого сырья

Проблема замены устаревшего оборудования на пищевых производствах неожиданно обострилась в последние годы в связи с необходимостью выполнения предъявляемых к нему требований по импортозамещению. В этих условиях потребовались принципиально новые подходы к совершенствованию традиционно применяемых машин и комплектующих их рабочих органов. Разработчики некоторых видов современного технологического оборудования в пищевых производствах пробуют использовать рабочие органы оболочечного типа, в которых эластичный рабочий элемент размещен на подкрепляющих опорах. Такого типа рабочие органы применяют для абразивной обработки при снятии жучков с некоторых видов промысловых рыб, например, ставриды или растительного сырья, в том числе нетрадиционного, такого как люпин или амарант [1].

Сечение рабочего органа в продольной плоскости симметрии показано на рис. 1, на котором изображен эластичный терочный элемент, размещенный на подкрепляющих ребрах жесткости.

Рис. 1. Принципиальная схема технологического рабочего органа оболочечного типа: 1 – ребро жесткости; 2 – эластичный терочный элемент

Fig. 1. The schematic diagram of a shell-type process tool:

1 – the stiffening plate; 2 – the elastic grating element

Для успешной эксплуатации такого типа рабочих органов, нагрузка на цилиндрическую поверхность которых зависит от геометрии обрабатываемого продукта, режимов обработки и физико-механических свойств самого материала оболочки, требуется создавать некоторое избыточное давление внутрь цилиндра. С этой целью необходимо проанализировать характер нагруженности внешней поверхности рабочего органа.

Материалы и методы

Рассмотрим круглый цилиндр, к которому перпендикулярно боковой поверхности приложены силы, симметричные оси. Такую схему нагружения конструкции удобно описать функцией напряжений ϕ, варьируемыми величинами в которой являются текущий радиус и центральный угол. Условия равновесия в этом случае удовлетворяются решением уравнения Пуассона d 29 + 1d9 + d29 _ 0 dr2   r drdz

в виде

ϕ = f(r)sinkz,(2)

где f принимает значения при изменении только r. После подстановки последней в выражение (1) для выражения f(r) получим дифференциальное уравнение второго порядка df + 1 f - k2 f = o.

dr ²    r dr

Для выражения решения этого уравнения применяют модифицированные функции Бесселя нулевого порядка разного рода, первого или второго, с аргументом kr. Для сплошного цилиндра тогда можно записать решение такого типа

f(r) = a 0 + a 1 r ² + a 2 r ² + a 3 r ³ + … .                                      (4)

Подставляя записанное соотношение в уравнение (3), получим довольно простые выражения для последовательных коэффициентов ряда

(2n)2 an – k2an – 1 = 0, или в другом виде k2             k2        k4

a = ₂ A o ;   a = 4 2 a = 2 . 4 ao.

Если подставить полученные соотношения в формулу (4), то получим

f ( r ) = a o

22   44     66

₁ kr kr kr

⁺ 2 2 ⁺ 2 2 ■ 4 2 ⁺ 2 2 ■ 4 2 ■ 6 2

В скобках в полученном соотношении оказывается выраженной функция Бесселя нулевого порядка от аргумента ikr. Она часто обозначается как I ₀ (kr). Ниже, по ходу изложения, будем использовать обозначение J ₀ (ikr) и приводить ее в таком виде

ϕ ₁ = a ₀ J ₀ (ikr)sinkz.

Дополнительные решения несколько отличаются от полученных решений уравнения (1). Например такое решение получают из записанной выше функции I0(ikr) продифференцированием с получением выражения dJ0 (ikr)     ikr .   к2 r 2     к4 r4        к6 r6

----------—--1 +---1--5--1--5—5--+ ...

d ( ikr )        2       2 ■ 4 2 ■ 4 2 ■ 6 2 ■ 4 2 ■ 6 2 ■ 8

Когда эту производную записывают с отрицательным знаком, то получают функцию Бесселя первого порядка, обозначаемую как J1(ikr). При дальнейших выкладках будем рассматривать функцию d                           k2 2

Fl (r) — r —Jo (ikr) — -ikrJ1 (ikr) — —— dr                       2

22    44

kr kr

1 +--- 1-----+ + ...

2 ■ 4 2 ■ 4 2 ■ 6

.

После дифференцирования получим, что

DU +¹ D7 - К ² 1 / 1 ( r ) = 2k ² J o (ikr ). dr    r dr     ;

Учитываем ранее полученное решение уравнения (3) в виде J ₀ (ikr). Дополнительно запишем, что f ₁ (r) в свою очередь удовлетворяет уравнению

( d ²    1 d ,₂) fd ² f 1 df , ₂ J _n

I + к ² 1 1       +       - k ² f l 1 = 0

^ dr    r dr     ) I dr r dr J и является его решением.

Окончательно решение уравнения удобно записать в виде

ϕ2 = a1sinkz(ikr)J1(ikr).(9)

Объединяя полученные решения (6) и (9), найдем функцию напряжений в следующей записи

ϕ = sinkz[a0J0(ikr) + a1(ikr)J1(ikr)].(10)

Такая функция напряжений, подставленная в ранее записанные уравнения, позволяет найти зависимости для компонент напряжений

σr = coskz[a0F1(r) + a1F2(r)], τrz = sinkz[a0F3(r) + a1F4(r)],(11)

где F 1 (r),…F 4 (r) – аналитические функции от r, содержащие J 0 (ikr) и J 1 (ikr). Применяя значения бесселевых функций из соответствующих таблиц, можно получать значения F ₁ (r),…F ₄ (r) для каждого r.

Обозначая a наружный радиус цилиндра, можно определить силы, приложенные к его поверхности, в виде следующих значений компонент напряжений

σ r = coskz[a 0 F 1 (a) + a 1 F 2 (a)], τ rz = sinkz[a 0 F 3 (a) + a 1 F 4 (a)].                         (12)

Подбирая значения постоянных k, a0, a1, легко исследовать наиболее характерные случаи симметричного нагружения цилиндра. Обозначим длину цилиндра через I и примем nn k = —, a0F1(a) + a1F2(a') = —An, a0F3(a) + a1F4(a) = 0.

Получаем значения постоянных a 0 и a 1 для случая, когда к боковой поверхности цилиндра приложено гармоническое нормальное давление A _n cos(n π z/I). Случай, когда n = 1, представлен на рис. 2. Таким же образом можно получить решение, когда вдоль поверхности цилиндра приложены касательные усилия величиной B _n sin(n π z/I).

Зададим значения n = 1, 2, 3… и получим, применяя принцип суперпозиции, решения задач, в которых давление нормальное поверхности цилиндра имеет такое распределение:

n z    .      2 n z    .      3 n z

A 1 cosy + A2 cos—— + A3 cos — +...,                            (13)

при этом для касательных напряжений можно записать ряд в виде nz       2nz       2nz

В sin-- + B, sin--- + В sin--- +... .                              (14)

1 _l 2 _l 3 _l

Если для функции напряжений ϕ вместо выражения (2) подставить соотношение

ϕ = f(r)coskz и следовать прежней логике, то вместо ранее полученного выражения получим функцию напряжений в другом виде

ϕ = coskz[b ₀ J ₀ (ikr) + b ₁ (ikr)J ₁ (ikr)].                                      (15)

Определенным выбором постоянных величин k, b 0 , b 1 можно добиться того, что решения для случая нормального давления, действующего на цилиндр, представляются рядом по синусам, а для касательных усилий – рядом по косинусам. Комбинируя различные решения, при необходимости можно получить любое осесимметричное распределение нормальных и касательных усилий по поверхности цилиндра. В то же время можно учитывать действующие усилия, распределенные по концам цилиндра [2; 3]. Накладывая простое растяжение или сжатие, мы всегда можем принципом суперпозиции получить результирующие этих усилий равными нулю, и в соответствии с принципом Сен-Венана их влиянием на распределение напряжений вдали от концов пренебречь [4]. Такие задачи при симметричном нагружении цилиндров решил Файлон. Конечные результаты его решения для случая, показанного на рис. 3, приведены ниже.

Цилиндр, длина которого равна πa, подвергается растяжению касательными усилиями, равномерно распределенными по указанным на рисунке частям поверхности. Представляет практический интерес распределение нормального напряжения σz по поперечным сечениям цилиндра. В таблице вычислены отношения этих напряжений к среднему растягивающему напряжению, полученному как отношение полного растягивающего усилия на площадь поперечного сечения цилиндра. Легко убедиться, что местные растягивающие напряжения вблизи нагруженных частей поверхности быстро убывают по мере удаления от указанных частей поверхности и приближаются к среднему значению [5].

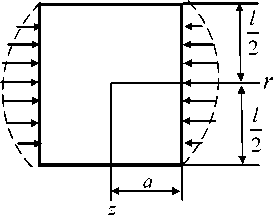
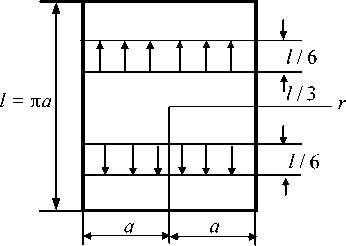
Рис. 2. Нагружение цилиндра при n = 1 Рис. 3. Нагружение цилиндра с исключением краевых зон

Fig. 2. Loading of the cylinder when n = 1          Fig. 3. Loading of the cylinder with the exception of the edge zones

Если производится посадка кольца на более длинный вал, то формулы расчета, предполагающие, что кольцо и вал, на который оно садится, имеют одинаковую длину, являются неточными. Намного точнее можно получить решение, рассматривая задачу, показанную на рис. 4, а, т. е. задачу для длинного цилиндра при равномерном нормальном давлении p, действующим на охватывающей части поверхности АВСD.

Таблица. Напряжения, вычисленные в зависимости от ширины зоны посадки Table. Stresses calculated depending on the width of the seating zone

z	r = 0	r = 0,2a	r = 0,4a	r = 0,6a	r = a
0	0,689	0,719	0,810	0,962	1,117
0,05	0,673	0,700	0,786	0,937	1,163
0,10	0,631	0,652	0,720	0,859	1,344
0,15	0,582	0,594	0,637	0,737	2,022
0,20	0,539	0,545	0,565	0,617	1,368

Искомое решение целесообразно получать, накладывая друг на друга решения для двух распределений давлений, показанных на рис. 4, б. Таким образом, основная задача, решение которой приводится ниже, состоит в определении действия знакопеременных давлений: p/2 на нижней половине цилиндрической поверхности и (–p/2) – на ее верхней половине.

A

C

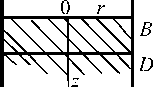
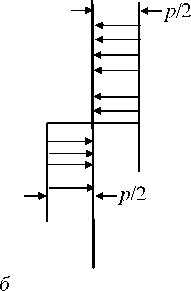
Рис. 4. Схема наложения элементарных решений Fig. 4. The scheme of superposition of elementary solutions

В качестве примера найдем функции напряжений, описываемые уравнением (15), записывая I 0 (kr) вместо J ₀ (ikr) и iI ₁ (kr) вместо J ₁ (ikr). Положим также b ₀ = ρ b ₁ . Тогда

ϕ = [ ρ I 0 (kr) – krI 1 (kr)]b 1 coskz.

Эта функция напряжений удовлетворяет уравнению равновесия при любых значениях k. Если считать, что k меняется в некоторой области, мы можем предположить, что b1 зависит от k и от приращения dk, и записать b1 = f(k)dk.

Подставляя это выражение в формулу (16) и складывая все полученные таким образом функции напряжений, получаем более общую функцию напряжений в форме

Ф = J [p I 0 ( kr ) - И ( kr )] f (k ) cos kzdk.                                (17)

Убедимся теперь, что можно выбрать функцию f(k) таким образом, чтобы рассматриваемая функция напряжений дала решение нашей задачи [6].

Результаты и обсуждение

Из развиваемых выше соображений и полученных формул непосредственно вытекает соотношение для касательного напряжения в виде trz = J [pkI0 (kr) - k 2rl\ (kr) - kI1 (kr) - 2k (1 - v)I0 (kr )]k2 f (k) cos kzdk, где штрих обозначает дифференцирование. Это соотношение оказывается равно нулю на поверхности r = a. Пусть выражение в скобках при r = a тоже равно нулю, тогда запишем уравнение для ρ в виде

P - ²⁽¹ -V ) + ka ^-—. -                                    ⁽¹⁸⁾

1 1 ( ka )

Здесь граничные условия имеют вид

p

Hr = — при r = a , z >  0,

²                                                            (19)

p

H r =- — при r = a , z <  0.

Значение σ r , выраженное из (17) для выше полученных зависимостей, примет вид

∞

°r

= -( (1 -2v-p) I o ( kr ) +\kr +y-| | ( kr ) k ³ f ( k )sin kzdk . n                        I kr ;

0 _

Вспомним теперь известную формулу

Умножив эти соотношения на p/ π , получим

∞ p sin kz — ----dk = ^{n J}0 ^k

7 sin kz

-----dk = 5 о ^k

П 2	при	z >  0,
0	при	z = 0,
П		z <  0.
2	при
■ p	при	z >  0,
0	при	z = 0,
- p	при	z <  0,

здесь значения справа представляют собой граничные величины для σ _r , определяемые формулами (21). Таким образом, выражение (20) удовлетворяется, если сделать правую часть уравнения (19) при r = a тождественно равной левой части приведенного ранее соотношения [7–8]. Это необходимо для выполнения условия

(1 - 2v - p) I ₀ ( ka ) +1 ka + — 1 1 1 ( ka ) V ka )

k ³ f ( k ) = p 1. n k

Оно служит для отыскания f(k), причем компоненты напряжения находятся по функции напряжений (17) с помощью выше приведенных формул. Они будут идентичны интегралам того же вида, что и интегралы в соотношении (21) для σ _r . Важно, что численные оценки, выполненные по (23), указывают на изменение напряжений в осевом направлении для разных значений радиального расстояния и дают изменение перемещений на поверхности.

Таким образом, если ширина равна радиусу цилиндра, а тангенциальное напряжение, сжимающее на поверхности и посредине нагруженной полосы, примерно на 10 % превышает приложенное давление [3; 9–10], то осевое напряжение σ _z на поверхности в месте окончания действия нагрузки становится растягивающим и составляет примерно 45 % от приложенного давления. Касательное напряжение τ _rz достигает наибольшего значения, равного 31,8 % приложенного давления, по концам нагруженной полосы АВ и СD (рис. 4) в точках, близких к поверхности [11].

Если давление прикладывается по всей криволинейной поверхности цилиндра, то независимо от его длины получаем просто сжимающие напряжения σ _z и σ _θ , равные приложенному давлению, и напряжения σ _z и τ _rz исчезают [12].

Заключение

Приведенные выкладки позволили рассмотреть несколько возможных ситуаций эксплуатации технологического оборудования. Проанализированные случаи нагружения цилиндрической поверхности неравномерной нагрузкой и сделанные в этом случае расчеты позволяют выбирать технологические режимы эксплуатации описанных выше рабочих органов предполагаемой конструкции. Наиболее успешно результаты проведенного моделирования могут быть использованы при выборе необходимых величин избыточного давления внутри используемого в новом оборудовании эластичного терочного элемента.