Оценка снизу нормы периодического функционала погрешности
Автор: Юмова Ц.Ж.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Функциональный анализ и дифференциальные уравнения
Статья в выпуске: 3, 2023 года.
Бесплатный доступ
Качество кубатурной формулы зависит от порядка сходимости нормы функционала ошибок. Формула, в зависимости от требуемой точности и сложности интегрируемой функции, считается хорошей, если с увеличением весовых коэффициентов и узлов разбиения уменьшается порядок сходимости нормы функционала ошибок. Действуя в рамках известного функционального подхода, предложенного С. Л. Соболевым, найдена нижняя оценка кубатурной формулы, суть которой заключается в минимизации погрешности формулы через норму соответствующего ей линейного функционала погрешности, действующего на пространстве подынтегральных функций. Построена специальная последовательность функций, определенная в некоторой области анизотропного пространства и имеющая компактный носитель, принадлежащий этой области. С помощью этой последовательности функций, усреднения индикаторной функции области с кусочногладкой границей и, учитывая характеристики специально выбранной экстремальной функции, получена нижняя оценка кубатурных формул.
Кубатурная формула, экстремальная функция, норма периодического функционала погрешности, порядок сходимости, оценка снизу
Короткий адрес: https://sciup.org/148327260
IDR: 148327260 | УДК: 517.518.87 | DOI: 10.18101/2304-5728-2023-3-23-33
Текст научной статьи Оценка снизу нормы периодического функционала погрешности
Кубатурная формула является одним из методов численного интегрирования, который позволяет приближенно вычислять значения определенных интегралов. Этот метод основан на аппроксимации интеграла суммой взвешенных значений функции в узлах разбиения интервала интегрирования. Существует множество различных методов вычисления весовых коэффициентов и узлов разбиения, в зависимости от требуемой точности и сложности интегрируемой функции. В целом, выбор конкретного метода кубатурной формулы зависит от конкретных требований к точности и сложности интегрируемой функции. Чем более сложная функция, тем более точный и сложный метод кубатурной формулы нужно использовать.
Среди исследований С. Л. Соболева по теории кубатурных формул, многие его работы, в частности, монография [1], посвящены оценкам погрешностей приближенного интегрирования функций в соответствующих пространствах. Умение эффективно вычислять многомерные интегралы по областям произвольных форм решаются различными методами и имеют важное прикладное значение в приложениях любого раздела математики. Эта задача вызывает широкий интерес в течение многих десятилетий и в работах учеников [2 - 5] и последователя [6] С. Л. Соболева рассматривалась, в частности, проблема убывания нормы функционала погрешности при увеличении числа узлов разбиения формулы.
Одним из основных показателей точности кубатурной формулы является ее порядок сходимости, определяющий как быстро уменьшается ошибка вычисления с увеличением числа узлов интегрирования. Чем выше порядок формулы, тем быстрее уменьшается ошибка и тем меньше узлов интегрирования необходимо для достижения нужной точности. Так, Н.С. Бахваловым [7] получена серия оценок по вероятности и доказано, что на классах функций в рассматриваемой области ф (x ) е C m ( A ), обладающих свойством дифференцируемости по координатным направлениям до порядка m k - 1 включительно, к = 1, n , имеющих кусочно-непрерывные частные производные порядка m k , порядок сходимости нижней оценки
• * 1
нормы функционала погрешности равен h , m = n ^ mJ . Этот поря-к=1 к док совпал с порядком сходимости верхней оценки, данной Н. М. Коробовым [8] для кубатурных формул, точных для конечных тригонометрических. В работе В. Л. Васкевич «доказана сходимость по норме на пространствах Соболева формул высокой тригонометрической точности. Также обоснована сходимость на пространствах функций дробной гладкости с учетом гладкости пространства подынтегральных функций и расположения узлов разбиения кубатурных формул» [2]. На основании гарантированной оценки, полученной в [3], В. Л. Васкевичем доказано, что погрешность приближенного значения интеграла не превосходит определенной величины для всех подынтегральных функций из рассматриваемого класса. В монографии Ц. Б. Шойнжурова [4] доказаны оценки норм функционалов ошибок с равномерным распределением узлов, действующих в пространстве Lm непериодических функций.
Объектом исследования служат формулы приближенного нахождения кратных интегралов. Целью исследования является получение нижней оценки нормы периодического функционала ошибок, являющегося разностью между интегралом и приближающей его линейной комбинацией значений, не зависящих от конкретной подынтегральной функции в узлах интегрирования и весах.
Веса же формулы почти везде одинаковы и отклоняются от константы лишь в узлах из некоторой приграничной области полосы интегрирования. Узлы кубатурной формулы расположены в вершинах параллелепи- педов, каждый из которых получается из любого посредством сдвига на некоторый многомерный вектор, причем указанные параллелепипеды не пересекаются и, будучи объединенными, покрывают в результате все пространство независимых переменных. Нумерацию узлов можно произвести с использованием мультииндекса в = (в1,в2,...,вn), имеющего целочисленные компоненты. Координаты любого узла можно найти по формуле x(в) = (x1,x2,...,Xn), Xk = hkPk, k = 1,.., n, а вектор (hx,h2,..,hn )eRn, компоненты которого суть длины ребер какого-нибудь параллелепипеда из выбранного разбиения, называется векторным шагом решетки. Координаты этого вектора связаны друг с другом посредством совершенно определенных зависимостей, зависящих от гладкости подынтегральной функции по соответствующим направлениям и порядка сходимости, определяемых с помощью системы соотношений hm1 = h2m2 = .к = hm = hm*.
Для достижения поставленной цели ставится задача подбора экстремальной функции, соответствующей периодическому функционалу ошибок и являющейся решением некоторого дифференциального уравнения с частными производными в обобщенных функциях. Новизна, полученной в работе нижней оценки нормы функционала ошибок для приближенного вычисления кратных интегралов, состоит в специальном подборе последовательности финитных функций на основании усреднений характеристической функции области с кусочно-гладкой границей с использованием свойств экстремальной функции.
Укажем ряд исследований с проблемами, схожими по постановке и направлениям, выполняемыми в теории квадратурных и кубатурных формул в настоящее время. В работе Васкевич В. Л. [9] получены оценки погрешности минимальных и почти минимальных кубатурных формул на классах периодических функций. Явные представления финитных функционалов в различных пространствах Соболева с последующим получением норм для оценки погрешности кубатурных формул представлены в исследованиях [10-12]. Вопрос хорошей обусловленности ненасыщаемых квадратурных формул, принципиально отличающихся от квадратурных отсутствием у них главного члена погрешности, рассмотрен Белых В. Н. в работе [13]. Различные постановки задач для квадратур изучены в трудах [14-16] зарубежных исследователей.
n
m* = n ^m 1 , А^ = { x G E« , 0 < xk < hk , k = 1, n } — фундаментальный
1tf k ) h n k k единичный куб, AhY — куб, полученный из куба Аh переносом на вектор hу объема hn, h0 = h | = -Jh2 + h22 +... + hn — модуль вектора h .
В качестве основных подынтегральных классов рассматриваются пространства функций, принадлежащих пространству L p во всем Е п , где 1< p <+» и имеющих по координатным направлениям x 1 , х2 ,.. .xn локально суммируемые с p - ой степенью несмешанные обобщенные производные Dmk ф заданных (ненулевых) порядков m 1 , m 2 ,. mn , также принадлежащих пространству L p во всем Е п . В определенных таким образом анизотропных пространствах W pm ( En ) для функций, обладающих свойством гладкости вдоль выбранного координатного направления, вводится естественная нормировка
1/ p
<^ . (1)
Известно [17], что пространство Wpm (En) при 1 < p <да является полным пространством, оно счетно и всюду плотно при 1 < p <ю, рефлек- о сивно и равномерно выпукло при 1 < p <ж . Пространство C” (En) бесконечно дифференцируемых финитных в En функций плотно в Wpm (En) при 1 < p <да, таким образом, его замыкание по норме (1) образует простран- о
ство W pm ( En ). В силу рефлексивности анизотропного пространства w m ( E n ) при 1 < p <№ всегда можно подобрать экстремальную функцию, соответствующую периодическому функционалу ошибок, которая будет иметь единичную норму. Тогда основная задача оценки погрешности ку-батурной формулы сводится к нахождению нормы функционала ошибок.
дифференцирования по каждой переменной в отдельности. Впервые Ц.Б. Шойнжуровым в [4] была подобрана экстремальная функция с введением специальной функции «шапочка», аналогом функции, рассмотренной в [18], но обладающей несколько иными свойствами.
О
Определим сходимость последовательности фп (x) с W” (О). Символ lim фп (x) = ф (x) будет означать, что на множестве Еп имеет место равно-П ^го мерная по x сходимость как самой последовательности, так и для последовательностей из несмешанных обобщенных производных Dm^kф задан ных порядков т1, m2,..., тп, также принадлежащих пространству Lp (Еп).
Z X ф ( X ) Ф п ( X ) =----- n
Так, последовательность основных функций вида где
Ф * ( x ) — функция «шапочка», сходится в Lp при п ^х к функции, тождественно равной нулю во всем Е п .
Аналогично методу, описанному в [4], построим последовательность
О финитных функций фп (x) с Wm (О) на основании усреднений характери стической функции области Q с кусочно-гладкой границей Г(О) и определим некоторые особенности экстремальной функции x * ,_ ,-?
Ф о I — | = h p Z exp(2 n ih" P ( x - У ))|2 пу| С у ,
V H ) у * 0
C Y =
n
= Ш-0'Z
Д h k = 0 Y* 0
D ”1 exp( - 2 n ih 1 уy ) ^ ( h - P )
+ h m k cr
p - i
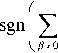
D”1 exp( - 2 n ih p y ) ^ ( h "'P )
+ № | dy ,
соответствующей периодическому функционалу ошибок, где его главный член в явном виде был получен в [19]:
% 0 f i | = 1 - Ф 0 f i | = 1 - Z det H 5 (x - Н у ).
V H) V H) у
Пусть функция Ф 0

достигает наибольшего значения в точках h p .
Из определения экстремальной функции имеем
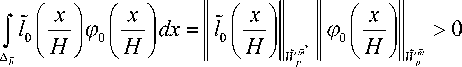
f x 1
Функция ф — периодическая с периодом hk , поэтому ее можно 0 V Н )
продолжить на все пространство, тогда нормы функции и ее продолжения будут совпадать
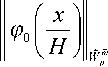
x
- x k
H
■г — w m
J l o l X I ^ 0 l XI dx = h n l C 0 - ^ 0 l x, ^I> h n ( C 0 - Ф 0 (0) ) ■
HHH
A h X 7 X 7 X X 7 J
Отсюда ф0 (0) > ф0 I — I ■ Обозначим через u I — разность между
0, hj , h функциями ф (0) и ф I — I, т.е. положим u| — I- ф0 (0) - ф0
0 0 , h j , h j 0
рем данную функцию так, чтобы она обладала следующими свойствами:
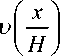
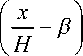
V I е R ,
u ( в ) = 0 и u I — |> 0, К H J
n p П
J u l — I dx - h n h m J JJ C( - 2 n i p ) mk |2 пв| mk exp( - 2 n i p x ) + C k0) dx ,(4)
A h К H J A k = 0 в 7 0 1
Обозначим
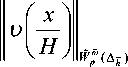
о h -o \ O h ,
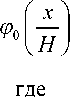
(1 + O ( h ))■ (5)
Wpm ( a h )
O h = { x eO , p ( x , E n \ O ) > 2 Lh } ,
Oh - {x e En, p(x, r(O)) < 2Lh}. Для получения нижней оценки нормы функционала ошибок воспользуемся функциями:
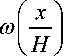
функция «шапочка», введенная в [4], yh (x) - h n J so.6 (y) ® ((x - y)h 1) dy — функция усреднения для области En
O 2 h , T h ( x ) = V h ( x ) u

— срезывающая функция.
Срезывающую функцию подберем так, что y h ( x ) - 1, если x eO 3 h , y h ( x ) < 1, если x eO 2 h и y h ( x ) - 0 в остальных точках x е En .
Лемма . Пусть область Q имеет кусочно-гладкую границу Г ( О ) . Тогда при стремлении модуля вектора h к нулю существует последователь-
О ность функций Ф; (x) с Wm (O) , для которой выполняются условия:
а) ф А ( x ) - 0, если x - h ^ или x ^O ^ h ;
б) I Ф п ( х ) dx - mes O
n
JJ(-1)m J
A hk - 0
в 7 0
D m^ e - 2 n ih APx ц ( h ~в )
*
+ h m Ck
p dx (1 + O(h)) .(6)
Доказательство .
Из
условия
леммы имеем
mes { x g Q , p (x , Г ) < Lh } = O ( h ).
Принимая во внимание свойства функции и
из (2 - 5) находим
j ф к ( x ) dx = j u f x ) dx (1 + O ( h )).
Q 3 h
Учитывая свойства функции u
вычислим последний интеграл
ju
Q’ h
x- I dx = mes Q h j ^ ( - 1 ) mk £
H ) д hk = 0 в * 0
x
n
h
в * 0
D m exp( - 2 n ih" P x ) , m r -----------------:--+ h C,
Ц ( h - 1 в ) k
p ’ dx. (8)
Из условия mes Q' = mes Q 3 h и из равенства (8) следует утверждение леммы.
3 Оценка снизу нормы периодического функционала ошибок в Wp m
Теорема. Пусть область Q имеет кусочно-гладкую границу Г(Q), sQ(х) — характеристическая функция, h0 — малый параметр. Тогда для любого периодического функционала погрешности кубатурных формул общего вида n l Q (x) = sQ (x)-££ hnDmk 5( x - hp)
веД k = 0
с узлами на вершинах параллелепипеда с шагом решетки h k вдоль выбранного координатного направления при стремлении модуля вектора h к нулю имеет место следующая оценка снизу
II l« с . .I m’«» Q p -1!I l ( x ) h ■<д> h" '(1 + O ( h ))■
Доказательство. Ранее была введена функция фк (x) в работе [4]. В за висимости от расположения точки x е En ее производная вдоль выбран ных координатных направлений будет равна:
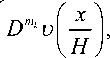
' если x gQ 3 h ,
|
D m‘ ^ h ( x ) = • |
0, |
если х £Q 2 h , |
|
D mk V h ( x ), |
если x g Q 2 h / Q 3 h |
О
Норму функции ф h ( x ) в W m ( П ) выразим через интеграл
n
IIФи(x)||p о = f ZIDmk Фи(xf dx • wm (n) П к=0
Разобъем область интегрирования на подобласти и рассмотрим интеграл в виде суммы двух интегралов
p dx,
имеем
П „к = 0
n
J 2 = f £| D mk Ф h ( x )| dx •
П и \ П h k = 0
Оценивая интеграл из (9) с учетом свойств функции и
J 1 = mes П 3 h
Ф 0

(1 + O ( h ))•
Wm ( A h )
Дифференцируя по формуле Лейбница под знаком интеграла (10), учитывая предположение о границе области О и оценку (7), находим
J 2 = Z fZ| D mk Ф и ( x ) p dx = O ( hm ' p^ (12)
Из (9), (10), (11) в^) ' полуЧим
II Фи ( x )lI wm "( П )
n
p
= ( mes П ) p fZ Z D k exp( - 2 n i P x ) ц ( в ) + C > (0) dx
^ д к = 0 в * 0
p m "
h p -41 + O ( h )) .(13)
Из представлений (6), (13) и асимптотического представления нормы функционала погрешности, окончательно имеем оценку снизу
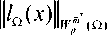
p p-1 . n
> ( mes П ) p fZ Z D mk exp( - 2 n i 0 x ) ц - 1( в ) + C ^0 dx
p hm "(1 + O (h ))•
^ д к = 0 в * 0
Теорема доказана.
Заключение
Теоретическая значимость работы заключается в том, что результаты исследовательской части могут быть использованы для вычисления кратных интегралов, когда прямое вычисление интеграла становится затруднительными.
Полученный новый результат уточняет ранее известные полученные оценки снизу, описанные во введении. Проведенная большая серия численных расчетов показала, что при вычислении многомерных интегралов по различным областям порядок сходимости нормы функционала, определяемых с помощью специальной системы соотношений, указывающей на связь гладкости подынтегральной функции вдоль соответствующих направлений с шагом решетки для функций анизотропного пространства совпадает с оценкой, полученной снизу для функционала ошибок.
Полученная нижняя оценка позволяет построить кубатурные формулы, учитывающие особенности интегрируемых функций для вычисления интегралов в пространствах большой размерности, когда вычисления интеграла «в лоб» становится вычислительно затратным или даже невозможным. Построенные кубатурные формулы могут применяться для решения задач математической физики, статистики, в различных областях науки и техники, в частности, для решения задач анализа поведения динамической системы и синтеза управляющих воздействий, сопутствующей этому процедуре дискретизации непрерывного движения системы. В целом, полученная нижняя оценка кубатурной формулы позволяет вычислять и оценивать интегралы с высокой точностью и учитывать особенности интегрируемых функций.
Список литературы Оценка снизу нормы периодического функционала погрешности
- Соболев С. Л. Введение в теорию кубатурных формул. Москва: Наука, 1974. 808 с.
- Васкевич В. Л. Сходимость кубатурных формул высокой тригонометрической точности в многомерных периодических пространствах Соболева // Математические труды. 2015. Т. 18, № 1. С. 3-14.
- Васкевич В. Л. Погрешность и гарантированная точность кубатурных формул в многомерных периодических пространствах Соболева // Сиб. матем. журн. 2014. № 55:5. С. 971-988. Б01: https://doi.org/10.1134/ 80037446614050024.
- Шойнжуров Ц. Б. Теория кубатурных формул в функциональных пространствах с нормой, зависящей от функции и ее производных: диссертация на соискание ученой степени доктора физико-математических наук (01.01.01, 01.01.07) / Вост.-Сиб. технол. ин-т. Улан-Удэ, 1977. 235 с.
- Шойнжуров Ц. Б. Оценка нормы функционала погрешности кубатурных формул в различных функциональных пространствах. Улан-Удэ: Изд-во Бурят. науч. центра СО РАН, 2005. 247 с.
- Рамазанов М. Д. Асимптотически оптимальный функционал ошибки над неизотропным гильбертовом пространством // Вопросы вычислительной и прикладной математики. Ташкент: Изд-во Ин-та кибернетики с вычисл. центром АН УзССР, 1972. Вып. 14. С. 72-82.
- Бахвалов Н. С. Численные методы. Москва: Наука, 1973. 631 с.
- Коробов Н. М. Теоретико-числовые методы в приближенном анализе. Москва: Наука, 1963. 224 с.
- Васкевич В. Л. Оценки погрешности минимальных и почти минимальных кубатурных формул на классах периодических функций // Сиб. электрон. матем. изв. 2018. № 15. С. 1080-1090. DOI: https://doi.org/10.17377/semi.2018.15.090.
- Корытов И. В. Линейный финитный функционал в весовом пространстве Соболева // Вестник Томского государственного университета. Математика и механика. 2023. № 81. С. 14-30. doi: 10.17233/19988621/81/2.
- Цыренжапов Н. Б., Урбаханов А. В. Общий вид финитных функционалов погрешности эрмитовых кубатурных формул в пространстве Соболева L" ( En ) // Вестник Бурятского государственного университета. Математика, информатика. 2017. № 4. С. 33-41. doi: 10/18101/2304-5728-2017-4-33-41.
- Жалолов О. И. Верхняя оценка нормы функционала погрешности кубатур-ной формулы Эрмита в пространстве С. Л. Соболева // Проблемы вычислительной и прикладной математики. 2017. № 3. С. 70-78.
- Белых В. Н. К вопросу хорошей обусловленности ненасыщаемых квадратурных формул // Сиб. электрон. матем. изв. 2021. № 18:2. С. 1083-1097. DOI: https://doi.org/10.33048/semi.2021.18.083.
- Shadimetov Kh. M., Hayotov A. R., Nuraliev F. A. (2013) On an optimal quadrature formula in Sobolev space L )m // Journal of Computational and Applied Mathematics. 243(1). P. 91-112. DOI: 10.1016/j.cam.2012.11.010.
- Hayotov A. R., Milovanovic G. V., Shadimetov Kh. M. (2014) Optimal quadrature formula in the sense of Sard in K2(P3) space // Publications de l'Institut Mathématique. 95(109). P. 29-47. DOI: 10.2298/PIM1409029H.
- Boltaev N. D., Hayotov A. R., Milovanovic G. V., Shadimetov Kh. M. (2017) Optimal quadrature formulas for Fourier coefficients in W^"1, D1) space // Journal of Applied Analysis and Computation. 7(4). P. 1233-1266. DOI: 10.11948/2017076.
- Бесов О. В., Ильин В. П., Никольский С. М. Интегральные представления функций и теоремы вложения. Москва: Наука, 1975. 480 c.
- Владимиров В. С. Уравнения математической физики. Москва: Мир, 1981. 512 с.
- Юмова Ц. Ж. Асимптотически оптимальные функционалы погрешности решетчатых кубатурных формул // Математические заметки СВФУ. 2015. Т. 22, № 3(87). С. 70-77.


