Оценка важности элементов инфраструктуры распределенной вычислительной системы при решении задач управления экономическим объектом

Автор: Горбачев Дмитрий Владимирович

Журнал: Инфокоммуникационные технологии @ikt-psuti

Рубрика: Новые информационные технологии

Статья в выпуске: 3 т.9, 2011 года.

Бесплатный доступ

С позиций архитектуры любая информационная система является распределенной системой обра- ботки информации. Инфраструктура ИС обеспечи- вает надежное исполнение бизнес-процессов пред- приятия. При этом роль элементов инфраструктуры ИС в реализации того или иного бизнес-процесса различна и может быть оценена по значению коэф- фициента важности элемента. Знание коэффициента важности позволит, в конечном итоге, организовать рациональное управление потоками информации и обосновать необходимый резерв оборудования.

Инфраструктура распределен- ной вычислительной системы, информационные потоки, структура, субстрат, концепт, источник информации, мера важности, ранг важности

Короткий адрес: https://sciup.org/140191494

IDR: 140191494

Текст научной статьи Оценка важности элементов инфраструктуры распределенной вычислительной системы при решении задач управления экономическим объектом

Инфраструктура современных распределенных вычислительных систем (РВС) предприятий представляет собой совокупность различных как по функциональному назначению, так и по принципам построения устройств. Однако общность в построении РВС все же имеется. Так, любая распределенная вычислительная система включает в свой состав следующие элементы: сервер обработки данных; сервер (или серверы) управления; сервер хранения данных; дополнительные серверы (прокси, печати, электронной почты); автоматизированные рабочие места сотрудников; подключаемые мобильные устройства; коммутаторы; маршрутизаторы; концентраторы; среда передачи данных.

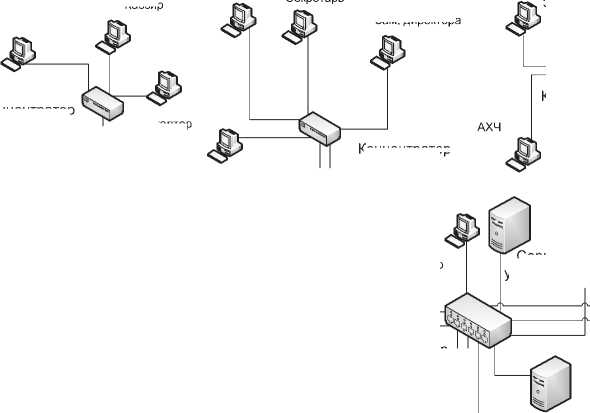
Часто встречающаяся модель распределенной вычислительной системы предприятия показана на рис. 1. Данная модель представляет собой инфраструктурную составляющую автоматизированной информационной системы (АИС) предприятия, в которой системообразующую роль играют потоки информации, циркулирующие между элементами в процессе функционирования.

Постановка задачи

Анализ структуры и содержания потоков информации, циркулирующей в АИС, позволяет разделить их на три основные группы:

- потоки, обеспечивающие структурную целостность системы;
- потоки, определяющие основные свойства системы;
- потоки автоматизации процессов.

В процессе функционирования системы потоки могут накладываться друг на друга или разветвляться, но в любом случае по маршрутам потоков можно оценить степень участия того или иного элемента системы в общем процессе функционирования. Оценка степени участия элемента может быть произведена по значению коэффициента важности КВ, отражающего значимость элемента системы при реализации IT-процессов в бизнес-системе предприятия. Знание КВ, в свою очередь, позволяет рациональным образом управлять загруженностью элементов системы, их техническим обслуживанием и ремонтом, а также рассчитывать необходимый горячий и холодный резерв оборудования. Таким образом, задача оценки важности элементов инфраструктуры РВС является актуальной и заключается в построении аналитической модели определения важности инфраструктурных элементов распределенной вычислительной системы по степени их участия в бизнес-процессах предприятия (организации).

Решение задачи

Исходя из того, что структура представляет собой совокупность устойчивых связей системы, обеспечивающих ее целостность и тождественность самой себе [1], информационные потоки бизнес-системы предприятия могут быть разделены на три основные группы:

- потоки коммуникаций элементов РВС;
- потоки, определяющие специфику применения РВС в составе информационной системы;
- потоки, возникающие при решении задач автоматизации бизнес-процессов и процессов принятия управленческих решений.

Потоки первой группы образуются из следующих составляющих:

- потоки, посылаемые участниками обмена информацией служебных запросов о состоянии компьютерной сети, количестве и активности абонентов, предоставляемых для общего использования ресурсах и получении ответов на эти запросы – служебный трафик. В различных архитектурах

АИС источниками и приемниками служебных запросов могут быть различные элементы. Так, в частности, при построении компьютерной сети на основе модели рабочей группы каждый компьютер посылает примерно одинаковый служебный трафик, запрашивающий ресурсы сети и сообщающий о доступных собственных ресурсах. При доменной модели реализуется более строгая схема коммуникаций, при которой инициатором обмена служебной информацией выступает контроллер домена. Поскольку информационные системы, использующие модель рабочей группы, как правило, сравнительно невелики (10-15 сетевых устройств), а также в силу того, что обычно они применяются для реализации узкой группы функций, в дальнейшем данная модель не рассматривается. Наибольший же интерес с точки зрения оценки взаимозависимости элементов АИС представляют различные варианты построения доменных моделей;

- потоки, определяемые передаваемой в процессе функционирования АИС информацией. Эта группа потоков имеет нерегулярный характер и формируется исходя из задач, решаемых пользователями АИС. Например, менеджер для формирования отчета по продажам может обращаться к нескольким базам данных. При этом его запросы физически проходят различные коммуникационные устройства, серверы и пр. Результаты об-
работки запросов, как правило, повторяют путь запроса, но только в противоположном направлении. Таким образом, маршрутами движения запросов и результатов определяется структурная связанность элементов системы.

Потоки второй группы обусловливают свойства системы, определяемые принадлежностью АИС к классу систем обработки данных (АСОИ), к автоматизированным системам управления (АСУ) или к автоматизированным информационно-поисковым системам (АИПС). К представителям АСОИ относятся системы бизнес-аналитики. Представителями АСУ являются, например, системы управления ресурсами предприятий: ERP, MRP, MRP II. К АИПС относятся библиотечные информационные системы.

Количественные и качественные характеристики потоков данной группы определяются спецификой содержания запросов пользователей и ответов на них и предопределяются процессами, протекающими в системе.

Потоки третьей группы определяются процессами автоматизации в АИС и формируются в соответствии с заложенными в ней программными алгоритмами обработки данных. Они определяют концептуальную целостность системы. Содержательная составляющая этих потоков определяется функциональным, математическим и программным обеспечением. Эти потоки возникают

Экономист

Директор Кассир

Секретарь

Зам. директора

Сервер управления

Резервный сервер

Бухгалтер

Нач. ОК

Администратор

Коммутатор

Специалист по кадрам

Отделы предприятия:

Управление;

Бухгалтерия;

Кадры;

Планирования;

Хозяйственный;

Склад;

Транспортный;

Цехи основного производства;

Отдел АСУ.

Концентратор (Hub)

Сервер обработки данных

Маршрутизатор

Концентратор

(Н ub)

Зав. гараж.

Маркетолог

Сервер цеха1

Сервер цеха2

Концентратор Склад (Hub)

nternet

Рис. 1. Модель распределенной системы предприятия

всякий раз, когда пользователь реализует некую, заранее запрограммированную, модель обработки информации.

Введение вышеуказанных групп потоков информации позволяет рассматривать РВС как некоторый объект, обладающий структурой, субстратом и концептом. Такой взгляд на систему способствует выделению элементов системы по степени важности по структуре, субстрату и концепту.

Концепция системного представления «важности» предполагает существенность различия аспектов системного рассмотрения объектов и системных параметров. Наряду с атрибутивными системными параметрами, значения которых характеризуют каждую отдельно взятую систему, существуют реляционные системные параметры, значения которых определяют отношения между объектами.

Одна система (один объект) может быть важнее другой (другого) по концепту, по структуре, по субстрату. Поэтому реляционный системный параметр «важнее», так же как и соответствующий ему атрибутивный, будет иметь векторный характер [2].

Пусть (w) ^^ [^ G77)]^3 – система, где m – субстрат (основа явлений, процессов, обусловливающих свойства системы); R – структура (совокупность устойчивых связей объектов); P – концепт системы (содержание понятия). Системное представление объекта дает возможность классифицировать различные типы оценок «важности» объектов в соответствии с тем, какие именно аспекты имеются в виду. В рассматриваемом случае выделяются структурная, субстратная, и концеп- туальную важности, сообразно тому, что именно оценивается: m, R или P.

Далее можно оценивать не m , R или P сами по себе, а некоторые отношения n -го порядка между элементами АИС.

Рассмотрим систему на рис. 1. Можно считать, что она относится к классу АСОИ, поскольку основными процессами, реализуемыми в ней, являются транзакционные процессы с базами данных (OLTP), процессы оперативной аналитической обработки (OLAP), процессы составления различных отчетов, а также документационные процессы. Основными процессами автоматизации являются:

- процессы бухгалтерского, складского, документационного учета и учета персонала;
- процессы проектирования и планирования производственных заданий, а также управления проектами;
- исследовательские и аналитические процессы.

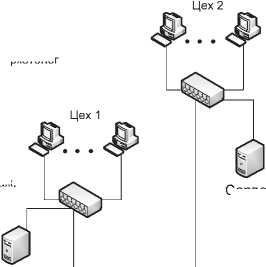
В топологической проекции модель распределенной сети предприятия (см. рис. 1) представляет собой некоторую древовидную структуру, на которую накладываются информационные потоки перечисленных процессов (см. рис. 2). Методика определения важности элементов системы состоит в следующем.

Составляется реестр отношений, предопределенных системообразующим отношением (то есть информационным), упорядоченный по количеству мест. Для обозначения отношения тождества каждого объекта самому себе используется знак «=». Отношение «источник» информации, обозначается символом «©». Пассивное отношение, то есть

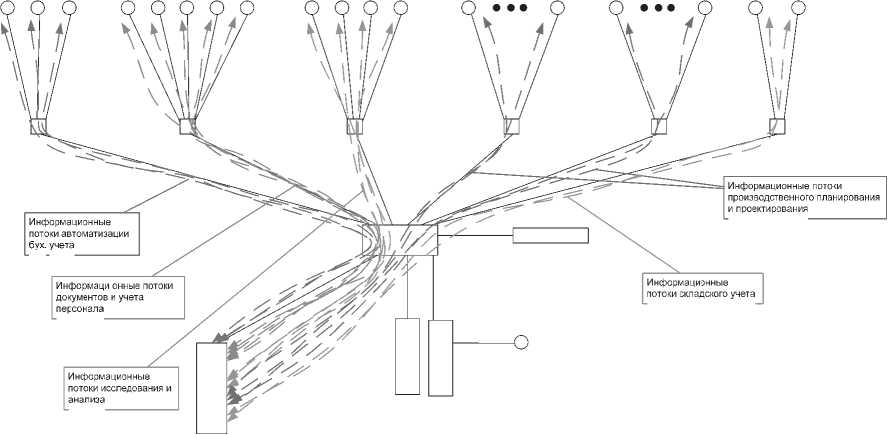
Рис. 2. Упрощенная схема основных потоков процессов автоматизации

Таблица 1. Шкала ранжирования

Степень важности

Определение

Пояснение

2; 4; 6; 8

Объекты несравнимы Объекты одинаково важны

Объект немного важнее

другого

Один важнее другого (сильное превосходство) Один явно важнее другого

Один абсолютно важнее другого

Значения, приписываемые промежуточным результатам

Сравнение объектов бессмысленно

Объекты имеют одинаковые информационные отношения (или соизмеримые)

Есть некоторое превосходство одного объекта перед другим на каком-либо уровне отношений

Существуют веские основания того, что один объект более важен, чем другой

Имеются неопровержимые основания, чтобы предпочесть один объект другому

Превосходство одного из объектов столь очевидно, что не может вызывать ни малейшего сомнения

Числа, обратные к вышеперечисленным Рациональные числа

Если при сравнении с объектом j объект i получил один из выше указанных рангов важности, то j при сравнении с i получает обратное значение

Получаются при арифметических операциях с числами данной шкалы

«приемник» информации, обозначается символом «0». При этом предпочтение всегда отдается «источнику информации» как элементу более активному по сравнению с «приемником информации».

Затем вводится понятие «экстенсиональной длины», которая определяется суммарным количеством активных отношений одного элемента системы к другим. Элементом системы, имеющим максимальный ранг важности, будет считаться тот, который будет иметь наибольшую экстенсиональную длину вектора отношений, или другими словами, который будет большее количество раз выступать «источником информации» по отношению к другим элементам системы. В другом предельном случае «важность» элемента АИС следует отождествлять с «пассивным» отношением к информации (то есть быть ее приемником).

После определения экстенсиональных длин векторов, присущих каждому элементу АИС, объектам различных типов присваивается определенный ранг важности в соответствии со шкалой (см. таблицу 1) и составляется матрица рангов важности [3].

При этом возможны следующие два случая: 1) если экстенсиональные длины превышают показания шкалы – в этом случае данному элементу присваивается максимальное значение важности, определяемое шкалой; 2) если экстенсиональные длины сравниваемых элементов получаются одинаковыми – в этом случае составляется новый реестр отношений, но уже между именно этими элементами АИС, и полученные результаты сводятся в матрицу А рангов важности. Данная матрица должна быть со- стоятельной, иметь единичный ранг, а также быть неотрицательной и неприводимой.

Тогда имеет место

где ^тах – наибольшее из собственных значений матрицы А . Уравнение (1) согласно теореме Перрона-Фробениуса имеет единственное (с точностью до постоянного множителя) неотрицательное решение to [4]. Значение to и принимается за коэффициент важности К _в элемента АИС. Для удобства и наглядности К _в нормализуется.

Применительно к объектам АИС системы методика определения меры «важности» имеет следующий вид. Пусть экстенсиональная длина L_i вектора информационных отношений элементов АИС определяется исходя из реестра отношений (см. рис. 3).

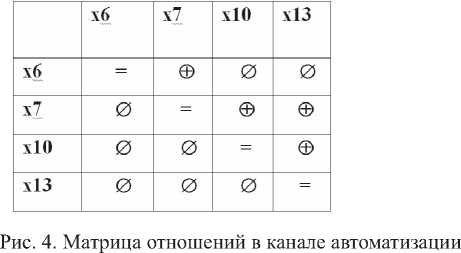
Как видно из рис. 3, L_i для {х6, х17, х23} и {х7, х8, х9, х18, х19, х20, х24, х25, х26} одинаковы. Поэтому составляется новый реестр отношений, но уже на основе отношений в системе канала автоматизации (см. рис. 4).

Таким образом, общие длины векторов Li для элементов всех типов равны: х7 = 8; х6 = 7; х3 = 5; х10 = 3; х13 = 2; х1 = 1; х2 = 1; х4 = 1; х5 = 1.

Далее составляется матрица А рангов важности (см. таблицу 2) и определяется набор ( to ₁ … to n ) значений важностей каждого из n элементов, а затем проводится сравнительная оценка полученных значений важностей. Элемент а_ij матрицы сравнений А дает оценку отношения to _i / to .

Для того, чтобы данная матрица была состоятельной, должны выполняться соотношения [5]:

а.. а ., = а., ,

ij jk ik ^,

(2)

и в частности

а.. = 1 и а .. = V •

Ч J¹ /а у

(3)

	xl	х2	хЗ	х4	х5	хб	х7	х8	х9	хЮ	Х11	Х12	х13	Х14	Х15	Х16	Х17	Х18	х!9	х20	х21	х22	х23	х24	X2i	х26
xl	=	0	©	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
х2	0	=	©	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
хЗ	©	©	=	0	0	©	0	0	0	0	0	0	0	0	0	0		0	0	0	0	0	0	0	0	0
х4	0	0	0	=	0	©	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
х5	0	0	0	0	=	©	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
хб	0	0	©	©	©	=		©		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
х7	0	0	0	0	0	©	=	0	0	©	©	©	©	©	0	0	0	0	0	0	0	0	0	0	0	0
х8	0	0	0	0	0	©	0	=	0	©	©	©	©	©	0	0	0	0	0	0	0	0	0	0	0	0
х9	0	0	0	0	0	©	0	0	=	©	©	©	©	©	0	0	0	0	0	0	0	0	0	0	0	0
х10	0	0	0	0	0	0	©	©	©	=	0	0	0	©	0	0	0	0	0	0	0	0	0	0	0	0
Х11	0	0	0	0	0	0	©	©	©	0	=	0	0	©	0	0	0	0	0	0	0	0	0	0	0	0
х12	0	0	0	0	0	0	©	©	©	0	0	=	0	©	0	0	0	0	0	0	0	0	0	0	0	0
Х13	0	0	0	0	0	0	©	©	©	0	0	0	=	©	0	0	0	0	0	0	0	0	0	0	0	0
Х14	0	0	0	0	0	0	©	©	©	©	©	©	©	=	0	0	0	©	©	©	0	0	0	©	©	©
х15	0	0	0	0	0	0	0	0	0	0	0	0	0	0	=	0	©	0	0	0	0	0	0	0	0	0
Х16	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	=	©	0	0	0	0	0	0	0	0	0
х17	0	0	©	0	0	0	0	0	0	0	0	0	0	0	©	©	=	©	©	©	0	0	0	0	0	0
х18	0	0	0	0	0	0	0	0	0	©	©	©	©	©	0	0	©	=	0	0	0	0	0	0	0	0
х19	0	0	0	0	0	0	0	0	0	©	©	©	©	©	0	0	©	0	=	0	0	0	0	0	0	0
х20	0	0	0	0	0	0	0	0	0	©	©	©	©	©	0	0	©	0	0	=	0	0	0	0	0	0
х21	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	=	0	©	0	0	0
х22	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	=	©	0	0	0
х23	0	0	©	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	©	©	=	©	©	©
х24	0	0	0	0	0	0	0	0	0	©	©	©	©	©	0	0	0	0	0	0	0	0	©	=	0	0
х25	0	0	0	0	0	0	0	0	0	©	©	©	©	©	0	0	0	0	0	0	0	0	©	0	=	0
Х26	0	0	0	0	0	0	0	0	0	©	©	©	©	©	0	0	0	0	0	0	0	0	©	0	0	=

Рис. 3. Матрица отношений (пример)

Таблица 2. Ранги важности элементов (пример)

,'V	х7	хб	хЗ	хЮ	х13	xl	х2	х4	х5
	=	4	5	7	8	9	9	9	9
хб	1/4	=	5/4	7/4	8/4	9/4	9/4	9/4	9/4
хЗ	1/5	4/5	=	7/5	8/5	9/5	9/5	9/5	9/5
хЮ	1/7	4/7	5/7	=	8/7	9/7	9/7	9/7	9/7
х13	1/8	4/8	5/8	7/8	=	9/8	9/8	9/8	9/8
xl	1/9	4/9	5/9	7/9	8/9	=	1	1	1
х2	1/9	4/9	5/9	7/9	8/9	1	=	1	1
х4	1/9	4/9	5/9	7/9	8/9	1	1	=	1
х5	1/9	4/9	5/9	7/9	8/9	1	1	1	=

Выполнение соотношения (3) необходимо для того, чтобы, определив, во сколько раз один объект важнее другого, можно было видеть, какую долю важности составляет второй объект от первого.

Легко видеть, что при состоятельности матрица А имеет единичный ранг, так как достаточно знать одну ее строку, чтобы вычислить все ос- тальные элементы. Причем а^ ^ О, для всех i. Нулевой результат попарного сравнения объектов означает, что они вообще не сравнимы, то есть не имеют информационной связи.

Для состоятельной матрицы А имеем:

И СО;

£ ац ---= и, i=\,..., и (4)

У=! toj причем n – это максимальное собственное значение А , а остальные ее собственные значения равны нулю, поскольку А имеет единичный ранг и сумма всех ее собственных значений равна следу матрицы.

^ТМ = ^,^aU⁼ⁿ ^. (5)

z = l

В общем случае можно считать, что набор

(top..®,;) должен удовлетворять уравнению (1). Тогда для неотрицательной

, 77 77

х Ах = У У а со. со, >0, У со, ,...,со ^ О . 1 , , i k i к 1’ ’ 77

7 = 1 ^ = 1

(где X = СО – вектор-строка из А) и неприводимой матрицы А существует единственное (с точностью до постоянного множителя) решение уравнения (1). Другими словами, при состоятель- ности А, взяв строку а., , а , ,..., а. и умножив а. на® а на il i2 in il 1 i2

0) , ... , а на о , получаем ® , co. co. .

2 7 7 in n i i i

Таким образом, умножая матрицу А на вектор CO , получим вектор n co . Следовательно, co является решением уравнения

Aco = neo.

В общем случае, умножая i -ую строку, как указано выше, можно не получить в точности co _i , co i ^… co _i из-за погрешностей в оценках a_ij . В теории матриц установлено [4], что собственные значения являются непрерывными функциями элементов. При малых возмущениях в элементах состоятельной матрицы наибольшее из собственных значений будет близко к n, а все остальные будут близки к нулю.

Таблица 3. Значения коэффициентов важностей элементов АИС (пример)

	х7	хб	хЗ	хЮ	х!3	х1	х2	х4	х5
К_в	0,114	0,045	0,045	0,115	0,102	0,102	0,236	0,13	0,11

Таким образом, насколько n окажется близко к ^тах , можно судить по решению уравнения (1). Именно поэтому для улучшения состоятельности рекомендуется соблюдать соотношение (3).

В результате из таблицы 2 получаем следующий набор векторов со : ®i = 61; ах = 15,25; ®3 = 12,2; со^ = 8,7; со5 = 7,6; сов = 6,7; coi = 6,7; cog = 6,7; сод = 6,7. Пронормировав со по и условию У(О{ =1, получаем численные значе-/=1

ния меры важности элементов АИС, выраженных коэффициентом важности (см. таблицу 3) [6].

Заключение

Одним из достоинств предлагаемой методики является то, что в ней не используются субъективные мнения экспертов, а весь аппарат строится на объективно существующих информационных отношениях между элементами системы. Знание точных численных значений важностей объектов системы и их количества в конечном итоге способствует принятию обосно- ванных решений при организации управления РВС. Кроме того, уже на ранних стадиях проектирования, когда только формируется облик новой системы, появляется возможность оценки вклада элемента каждого типа в эффективность системы в целом с целью правильного распределения акцентов при разработке подсистем резервирования. Работа выполнена в рамках Государственного контракта №02.740.11.0666 (шифр заявки 2010-1.1-215-033-032).

Список литературы Оценка важности элементов инфраструктуры распределенной вычислительной системы при решении задач управления экономическим объектом

Лищинский Л.Ю. Структурный и параметрический синтез гибких производственных систем. М.: Машиностроение, 1990. -312 с.
Уемов А.И., Мамчур Е.А. и др. Принцип простоты и меры сложности. М.: Наука, 1991. -302 с.
Саати Т.Л. Математические модели конфликтных ситуаций. Пер. с англ. М.: Сов. радио, 1977. -304 с.
Беллман Р. Введение в теорию матриц. М.: Наука, 1969. -367 с.
Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука, 1978. -832 с.
Горбачев Д.В. Обоснование технологии ремонта изделий РЭА боевых средств ЗРС фронтового звена за счет оптимизации структуры системы ТО и ремонта. Дисс. к.т.н. СПб.: СП-ВЗРКУ, 1997. -300 c.

Статья научная