Оценка влияния неудерживающих связей на величину динамических реакций балочного моста

В последнее время становятся достаточно актуальными расчеты строительных сооружений на различные виды динамических воздействий, в том числе у которых продолжительность воздействия очень мала, а интенсивность эффективного избыточного давления во фронте ударной волны может достигать десятков МПа. Цель данного исследования – получить численные данные влияния неудерживающих связей на пролетное строение мостового перехода при динамических воздействиях. Рассмотрим задачу кратковременного динамического воздействия в виде прямо- угольного импульса на пролетную часть мостовой балочной конструкции, частично опирающейся на упругое односвязное основание, воспринимающее только сжимающие напряжения. Для таких конструкций граничные условия в процессе колебаний меняются, что является следствием наличия неудерживающих связей по линии контакта конструкции с основанием [1, 2].

Расчетная модель и метод расчета

Расчетная схема пролета балочного моста методом конечных элементов (МКЭ) при действии кратковременной динамической нагрузки приведена на рисунке 1.

^F(t)

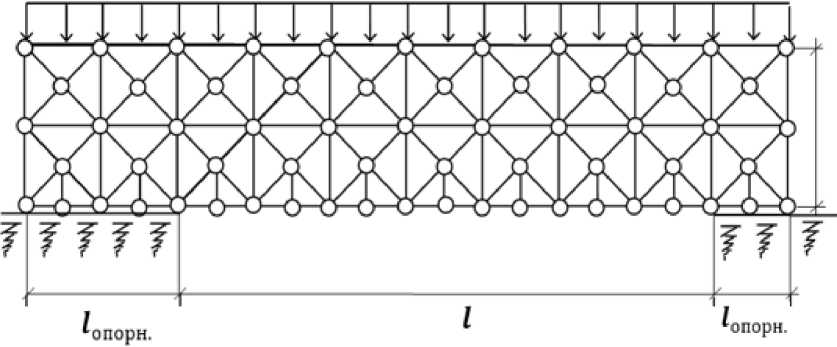
Рис. 1. Расчётная схема метода конечных элементов

Применяем стандартную процедуру МКЭ. При этом, разделим все конечные элементы на те, которые не контактируют с основанием, и на элементы, которые с ним контактируют [2]. Матрицы жесткости для первых формируются стандартно, для вторых – по предлагаемой ниже методике.

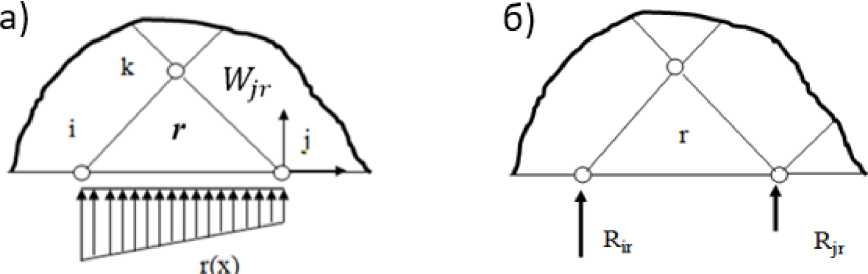
Рис. 2. Расчетные схемы для конечных элементов, контактирующих с основанием: а) линейная функция реакции основания, б) дискретные реакции в узлах

Рассмотрим конечный элемент, показанный на рисунке 2. Вертикальные перемещения по линии контакта конструкции с основанием аппроксимируем линейной функцией. В этом случае последняя может быть выражена через составляющие узловых перемещений конечного элемента:

W(x) = Wir(1~)

+ W-x

(1 )

где Wi_r, Wj_r - вертикальные составляющие перемещений i-го и j-го узлов r -го конечного элемента;/ - длина стороны конечного элемента, контактирующей с основанием.

В случае упругого основания, способного воспринимать сжимающие и растяги- вающие напряжение, реакция основания r(x) распределена по всей стороне треугольника. Распределенная реакция основания, принимаемая с учётом гипотезы Винклера, может быть заменена эквивалентной системой двух узловых сил:

I

Rir = -[ r(x)xdx = -^(2Wir + Wjr)(2)

I6

0 i 1

Rjr = 7 I r(x)(1 — x)dx = —— (2Wir + Wjr)(3)

где Cw - коэффициент податливости основания.

Неизвестные силы Rir, Rjr действуют одновременно с заданными внешними узловыми силами Fir, Fjr. Неизвестные функции перемещений узлов конечноэлементной модели определяются из ре- шения системы обыкновенных дифференциальных уравнений движения и уравнений связи между реакциями и перемещениями в узлах контакта балки и упругого основания [3, 4]. В матричной форме:

(MZ + CZ + KZ = F + R,

I          R = -DZ,

(4 )

где М, С, К – матрицы масс, вязкости и жесткости системы.

Z,Z,Z - искомые векторы перемещений, скоростей и ускорений;

D – матрица жесткости основания, элементы которой зависят от механических характеристик основания и размеров сетки конечных элементов, F(t) – вектор внешней нагрузки.

В случае упругого основания, способного воспринимать только сжимающие напряжения, реакция основания может распределяться не по всей стороне конечного элемента (рис. 3). Длина площадки контакта /cont неизвестна. В целом задача становится конструктивно нелинейной. Неизвестное значение lcont= l(n) и все узловые неизвестные на каждом шаге по времени определяются итерационным способом из условия отсутствия растягивающих напряжений по линии контакта из условия:

I/0+1) _ Дп) I

Y'cont     Lcont\ < с

Здесь n – номер итерации всей системы уравнений движения конечно-элементной модели на отрезке времени [ti ; ti+1 ];

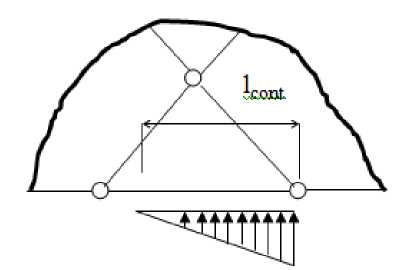
Рис. 3. Расчетная схема для конечных элементов c переменной зоной контакта с основанием

ε – заданная точность выполнения условия

Результат прямого динамического расчета

Интегрирование системы дифференциальных уравнений МКЭ производим методом квадратичного ускорения, в котором для большей точности решения неизвестная функция ускорения в пределах двух смежных временных шагов аппроксимируется квадратной параболой. Программная реализация упомянутой процедуры выполнена средствами пакета MATLAB.

На рисунке 4 приведены результаты расчета в виде графиков колебаний центра пролета высокой балки (h=1м., l= 9м., EI= 4.9Л06 кН-м2, F(t) = 18 МПа) при различных граничных условиях по линии контакта с основанием на действие внезапно приложенной динамической нагрузки. Время действия кратковременной нагрузки составляет 0.008 с.

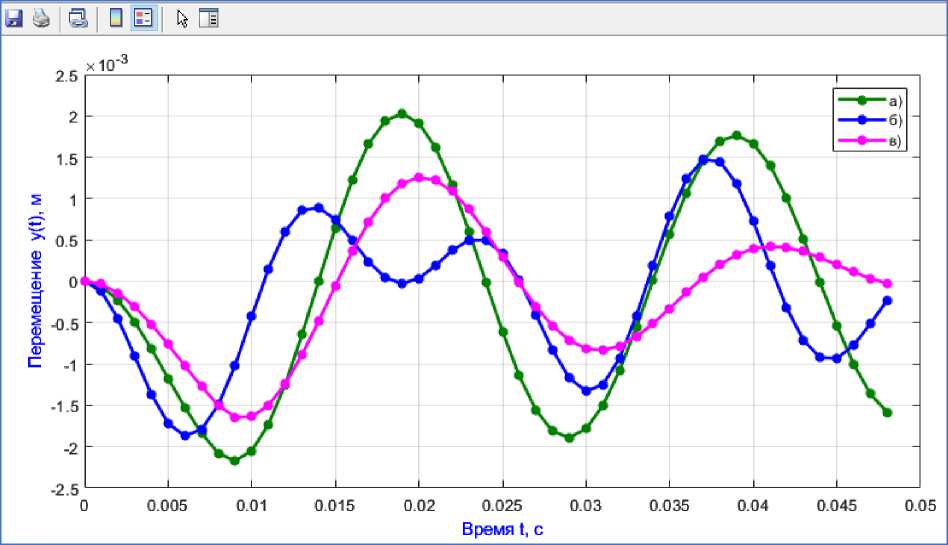
Рис. 4. График нестационарных колебаний центра балочного пролета: а – односвязное податливое основание, б – двухсвязное податливое основание, в – без учета податливости основания

Заключение

Учёт податливости основания для ис- ходных данных конкретного примера расчета балочного пролета моста на кратко- временную динамическую нагрузку показало увеличение максимального прогиба на 17% и практически не повлияло на время его достижения. Все это требует необ- ходимости применения таких расчетных моделей взаимодействия сооружения и ос- нования для рассмотренного вида динамических расчетов.