Оценка влияния сезонности на корректировку ингредиентов продуктов питания

DOI:

εi=yi – yi,      i=1÷n удовлетворяла свойствам случайной компоненты ряда, а именно отвечала условиям:

• а)    случайность колебания уровней остаточной последовательности;

• б)    соответствие распределения случайной компоненты нормальному закону распределения;

• в)    равенство нулю математического ожидания случайной компоненты;

• г)    независимость значений уровней случайной компоненты.

В этом случае можно ставить задачу о построении уравнения регрессии, с помощью которого в дальнейшем может осуществляться управление процессами производства продуктов питания наибольшей пищевой и биологической ценности, анализ влияния на этот параметр различных составов ингредиентов и их свойств.

В данной работе, в качестве примера, рассматривается производство корма для непроизводительных животных:

• -    y i – пищевая и биологическая ценность корма (баллы);

• -    x 1i – суммарное количество ингредиентов (кг);

• -    х 2i - период производства (дней);

• -    x 3i - среднее содержание важнейших витаминов, таких как С, А и минеральных веществ, в частности Са (мг/кг.).

Для выбранной модели требуется найти коэффициенты линейной модели уравнения множественной регрессии вида:

у = а о + b 1 х 1 + b 2 x 2 + Ь 3 х 3 (1) где у - пищевая и биологическая ценность корма; а 0 - свободный член уравнения регрессии; b 1 , b 2 , b 3 - коэффициенты уравнения регрессии при соответствующих показателях, соответственно.

Эти параметры неизвестны и для их нахождения необходимо провести ряд вычислений [1].

Значения x i и у содержат ошибки, так как учитываются не все факторы, влияющие на y.

Значения величин y i , x 1i , x 2i , x 3i даны в таблице 1 .

Необходимо найти зависимость между представленными параметрами и, если таковая есть, построить уравнение множественной регрессии, которое как можно лучше аппроксимирует исходный статистический материал.

Уравнение регрессии тем точнее, чем больше статистический материал, используемый при его построении (если существует реальная связь).

Т а б л и ц а 1

Исходные данные о свойствах корма

№ набл.	Пищевая и биологическая ценность корма (y)	Суммарное количество ингредиентов (x 1 )	Период производства. (x 2 )	Среднее содержание важнейших витаминов, и минеральных веществ (x 3 )
1	205,17	30	100	4,4
2	187,99	32	120	3,3
3	247,2	37	170	6,05
4	456,4	55	230	12,1
5	601,4	65	350	19,25
6	265,4	33	170	4,95
7	207,6	35	150	1,815
8	401,9	40	260	12,1
9	679,9	69	470	17,05
10	950,7	77	550	24,2
11	560,8	65	356	13,75
12	940,79	80	771	22,55
13	874,36	63	333	36,3
14	695	41	128	39,05
15	998,66	95	781	15,4
16	729,32	71	357	25,85
17	946,89	67	444	31,35
18	617,4	45	269	19,8
19	1190,57	79	666	39,05
20	358,1	34	212	9,9

Дана выборка из 20 наблюдений с известными значениями Y, X 1 ,X 2 и X 3 .

В работе предполагается построить уравнение регрессии типа (1).

Сравнительная оценка влияния различ- ных факторов (хji) на пищевую и биологическую ценность (уi) и взаимосвязи факторов между собой проводится с использованием значений парных коэффициентов корреляции (r). Для этой цели строили таблицу 2.

Т а б л и ц а 2

Матрица коэффициентов парной корреляции

	Пищевая и биологическая ценность (y)	Суммарное количество ингредиентов (x 1 )	Период производства. (x 2 )	Среднее содержание важнейших витаминов, и минеральных веществ (x 3 )
Пищевая и биологическая ценность (y)	1,00
Суммарное количество ингредиентов (x 1 )	0,89	1,00
Период производства. (x 2 )	0,85	0,93	1,00
Среднее содержание важнейших витаминов, и минеральных веществ (x 3 )	0,84	0,56	0,46	1,00

Для нахождения матрицы коэффициентов парной корреляции используем табличный редактор «Excel», выполнив следующие команды: «Сервис» — «Анализ данных» - «Корреляция». Затем в диалоговом окне «Корреляция» в поле «Входной интервал» вводим адреса ячеек таблицы №1, включая названия реквизитов. Установив отметки в окне «Метки в первой строке» и «По столбцам», выбираем параметр выбора «Новый рабочий лист».

Для проверки значимости коэффициентов парной корреляции используют t-критерий Стьюдента. Для этой цели требуется найти для каждого коэффициента парной корреляции значение t-критерия Стьюдента.

Полученные данные занесем в таблицу 3.

Т а б л и ц а 3

Проверка значимости коэффициентов парной корреляции с использованием t-критерия Стьюдента

	Пищевая и биологическая ценность (y)	Суммарное количество ингредиентов (x 1 )	Период производства. (x 2 )	Среднее содержание важнейших витаминов, и минеральных веществ (x 3 )
Пищевая и биологическая ценность (y)	1
Суммарное количество ингредиентов (x 1 )	8,08	1
Период производства. (x 2 )	6,9	10,52	1
Среднее содержание важнейших витаминов, и минеральных веществ (x 3 )	6,55	2,86	2,17	1

Далее необходимо сравнить t ф для каждого коэффициента парной корреляции с t-критическим (табличное значение) для 5 % уровня значимости (двустороннего) и числа степеней свободы ν = n - 2 (в нашем случае ν = 18).

Если t ф > t кp , то найденный коэффициент парной корреляции признается значимым. Данное действие выполняется с помощью логической функции «ЕСЛИ»:=ЕСЛИ (В7>$G$7; "значимый"; "незначимый").

Т а б л и ц а 4

Сравнение t ф и t кp

Коэффициенты парной корреляции	Значение t -критерия Стьюдента	t критическое для 5% уровня значимости и числа степеней свободы ν =n-2	Значимость коэффициента парной корреляции
r ух1	8,08	2,1009	значимый
r ух2	6,9		значимый
r ух3	6,55		значимый
r x1x2	10,52		значимый
r x1x3	2,86		значимый
r x2x3	2,17		значимый

В модель уравнения регрессии включаются только те факторы, которые имеют коэффициент парной корреляции r ухj > 0,5. Но по величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов, т.е. линейная зависимость между переменными. Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, то если факторы явно коллинеарны (r xixj > 0,8), они дублируют друг друга и один из них рекомендуется исключить из регрессии. При этом в модель включается фактор, который более тесно связан с результатом [2].

Данное требование позволяет избежать явления мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

В связи с этим, в модель уравнения множественной регрессии включаются факторы Х 2 , и Х 3 , а исключается соответственно фактор Х 1 .

Произведем построение уравнения регрессии вида (1) с учетом оставленных для дальнейших исследований факторов xji. Для построения статистической модели, характеризу- ющей значимость и точность найденного уравнения регрессии, используем табличный процессор «Excel», применив команды «Сервис» -«Анализ данных» - «Регрессия».

В диалоговом окне «Регрессия» в поле «Входной интервал Y» вводим данные по « пищевой и биологической ценности », включая название реквизита. В поле «Входной интервал X» вводим данные по выбранным влияющим факторам ( период производства и среднее содержание важнейших витаминов, и минеральных веществ). При этом вводимые данные должны находиться в соседних столбцах. Затем устанавливаем флажки в окнах «Метки» и «Уровень надежности» . Установим переключатель «Новый рабочий лист» и поставим флажки в окошках «Остатки» . После всех вышеперечисленных действий нажимаем кнопку «ОК» в диалоговом окне «Регрессия». Далее производим форматирование полученных результатов расчета коэффициентов уравнения регрессии и статистических характеристик и получаем таблицы 5, 6, 7, 8.

Таким образом, искомое уравнение регрессии имеет вид:

Y = 41,02 + 0,87x 2 + 14,84x 3 (2)

Полученное уравнение описывает искомую зависимость пищевой и биологической ценности (у) от периода производства (x 2 ) и среднего содержания важнейших витаминов и минеральных веществ (x 3 ). Получаем таблицы 5, 6, 7, 8.

Т а б л и ц а 5

Регрессионная статистика
Множественный R	0,99
R-квадрат	0,98
Нормированный R-квадрат	0,98
Стандартная ошибка	43,27
Наблюдения	20

Т а б л и ц а 6

Диспе			рсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	1778334,22	889167,11	474,81	1,21369E-15
Остаток	17	31835,25	1872,66
Итого	19	1810169,47

В таблице 6 df - число степеней свободы, которое определяется по формуле: df = n - (k + 1) , где n - число строк в таблице исходных данных (в данном случае n = 20); k - число аргументов.

F - критерий Фишера. Значимость F - вероятность принятия «нулевой гипотезы» по всему уравнению в целом.

Т а б л и ц а 7

	Коэффициенты	Стандартная ошибка	t-статистика	P-значение	Нижние 95 %	Верхние 95 %	Нижние 99 %	Верхние 99 %
Y-пересечение	41,02	20,75	1,98	0,06	-2,75	84,79	-19,10	101,15
Фондовооруженность (x 2 )	0,87	0,05	16,39	7,49288E-12	0,76	0,98	0,71	1,02
% прибыли (x 3 )	14,84	0,94	15,76	1,41681E-11	12,86	16,83	12,11	17,58

В таблице 7 показатель Р-Значение - это вероятность принятия «нулевой гипотезы» по каждому коэффициенту. В рассматриваемой задаче нулевую гипотезу можно отвергнуть [3].

Коэффициенты представляют собой значения свободного члена уравнения регрессии и коэффициентов уравнения регрессии.

t-статистика находится как отношение столбца «Коэффициенты» к столбцу «Стандартная ошибка».

Нижние 95 % и верхние 95 %, а также нижние 99 % и верхние 99 % - границы нахождения значений коэффициентов регрессии. Значения считаются экономически достоверными, если лежат в достаточно узком однознаковом диапазоне. Коэффициенты рассматриваемой регрессии удовлетворяют этому требованию.

Т а б л и ц а 8 Выход остатка

Наблюдение	Предсказанная пищевая и биологическая ценность (y)	Остатки
1	193,13	12,04
2	194,16	-6,17
3	278,38	-31,18
4	420,27	36,13
5	630,56	-29,16
6	262,05	3,35
7	198,15	9,45
8	446,31	-44,41
9	702,05	-22,15
10	877,63	73,07
11	554,12	6,68
12	1044,93	-104,14
13	868,93	5,43
14	731,84	-36,84
15	947,46	51,20
16	734,62	-5,30
17	891,78	55,11
18	568,43	48,97
19	1198,76	-8,19
20	371,99	-13,89

Уравнение линейной регрессии будем определять для выбранных влияющих факторов. Оно имеет вид:

y=41,02+0,87x 2 +14,84x 3 (3)

После построения уравнения регрессии целесообразно оценить достоверность полученной зависимости [4].

Проверка гипотезы по правильности выбора уравнения регрессии включает исследование случайности отклонений фактического и расчетного значений у.

Характер этих отклонений изучается с помощью ряда непараметрических критериев. Одним из таких критериев является критерий серий, основанный на медиане выборки. Ряд из величин ε i располагают в порядке возрастания их значений и находят медиану ε m , полученную из вариационного ряда, то есть срединное значение при n нечетном или среднее арифметическое из 2-х соседних срединных значений при четном n . Возвращаясь к исходной последовательности ε i и сравнивая значение этой последовательности с E m , ставят знак “+”, если E i > E m и знак “-”, если E i < E m . Соответственно значение

ε i опускается, если ε i =ε m . Таким образом, получается последовательность, состоящая из «+» и «-», общее число которых не превосходит n.

Последовательность подряд идущих «+» или «–» называется серией. Для того чтобы последовательность ε i была случайной выборкой, протяженность самой длинной серии не должна быть слишком большой, а общее количество серий слишком малым. Обозначим протяженность самой длинной серии K max , а общее число серий через v . Выборка признается случайной, если выполняются следующие неравенства для 5 %-го уровня значимости:

2 v >

1( n + 1 - 1.96 V n - 1)

K max <[ 3,3 lg(n+1) ] , где квадратные скобки означают целую часть числа.

Если хотя бы одно из этих неравенств нарушается, то гипотеза о случайном характере отклонений уровней ряда от теоретических уровней отвергается и модель признается неадекватной.

В рассматриваемой задаче:

Медиана ε m = (-5,3+3,35)/2= -0,98.

Т а б л и ц а 9

Разница между прогнозируемыми и экспериментальными результатами

Предсказанная производительость (у)	Остатки		Остатки в порядке возрастания
193,13	12,04	+	-104,14
194,16	-6,17	-	-44,41
278,38	-31,18	-	-36,84
420,27	36,13	+	-31,18
630,56	-29,16	-	-29,16
262,05	3,35	+	-22,15
198,15	9,45	+	-13,89
446,31	-44,41	-	-8,19
702,05	-22,15	-	-6,17
877,63	73,07	+	-5,30
554,12	6,68	+	3,35
1044,93	-104,14	-	5,43
868,93	5,43	+	6,68
731,84	-36,84	-	9,45
947,46	51,20	+	12,04
734,62	-5,30	-	36,13
891,78	55,11	+	48,97
568,43	48,97	+	51,20
1198,76	-8,19	-	55,11
371,99	-13,89	-	73,07

Протяженность самой длинной серии K max < 4.

Общее число серий через v > 6.

Так как оба условия выполняются, то гипотеза о случайном характере отклонений уровней ряда от теоретических уровней принимается и модель признается адекватной [5].

Данная проверка производится обычно приближенно с помощью нахождения показателей ассиметрии у т и эксцесса Y 2 . Это производится на основании сравнения найденных показателей

6( n — 2)

( n + 1)( n + 3)

с теоретическими. При нормальном распределении некоторой генеральной совокупности показатели асимметрии и эксцесса должны быть равны 0 ( Y 1 =0, Y 2 =0). При конечной выборке из генеральной совокупности показатели асимметрии и эксцесса имеют отклонения от 0.

Для оценки соответствия выбранной совокупности данных нормальному закону распределения используется так называемая оценка показателей эксцесса и асимметрии.

В качестве оценки показателя асимметрии используются формулы:

⁽/ n ) | ^g 3                        (5)

(1/ n ) ± ( е 2 )³

/      i = 1

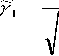
для оценки показателя эксцесса:

ГТ ~

^Y 2

24 n ( n — 2)( n — 3)

( n + 1)²( n + 3)( n + 5)

(1/ n ) j n; е_г⁴

^Y 2 =    /   n =1 _{7 7}

(1 n ) Z ( е_г ²)² /      i = 1

I ~ <  1,5 ^

Если одновременно выполняются неравенства для 5 % уровня значимости 0-ой гипотезы, то считается, что фактическая кривая распределения допустимо близка к кривой нормального распределения. Если выполняется только одно неравенство, то с вероятностью более 5 % можно утверждать, что фактическая кривая распределения недопустимо отклоняется от кривой нормального распределения. Следовательно, адекватности представленных моделью данных нет.

Другие случаи требуют дополнительной проверки при помощи более сложных критериев.

Проведем указанные проверки.

~

Y 2

+-- n +1

< l,⁵ ^.

Условия выполняются, следовательно гипотеза о нормальном распределении случайной компоненты принимается.

Проверка равенства математического ожидания случайной компоненты нулю осуществляется на основе t -критерия Стьюднта.

Если расчетное значение меньше табличного значения при принятом уровне значимости нулевой гипотезы, то математическое ожидание случайной компоненты генеральной совокупности равно нулю.

В противном случае – отвергается, и модель считается неадекватной. Число степеней свободы v=n-1. Так как tрасч< tтабл , то гипотеза о равенстве 0 математического ожидания случайной последовательности принимается и модель признается адекватной [6]. Далее для выявления существующей автокорреляции остаточной последовательности осуществляется следующая проверка зависимости последующего значения от предыдущего. Эта проверка может производиться по ряду критериев.

Наиболее распространенным является d -критерий Дарвина-Уотсона. Расчетное значение этого критерия находится по формуле:

∑ ⁿ ( ε i - ε i - 1 ) ² d ₌ i = 2                ,

ⁿ ∑ ^ε i ² i = 1

Т а б л и ц а 10

Значения критериев Дарвина-Уотсона

n	p=1		p=2		p=3
	d1	d2	d1	d2	d1	d2
15	1,08	1,36	0,95	1,54	0,82	1,75
20	1,20	1,41	1,1	1,54	1,00	1,68
30	1,35	1,49	1,28	1,57	1,21	1,65

Если расчетное значение критерия d больше верхнего табличного значения d 2 , то гипотеза о независимости уровней остаточной последовательности, то есть об отсутствии в ней автокорреляции принимается с вероятностью 95 %.

Если расчетное значение d меньше нижнего табличного d 1 , то эта гипотеза отвергается и модель считается неадекватной.

Если значение d находится между значениями d 1 и d 2 , включая сами эти значения, то считается, что нет достаточных оснований делать тот или иной вывод и необходимы дальнейшие исследования, например, по большему числу наблюдений.

В данной задаче: d =2,25 - критерий Дарвина-Уотсона. Расчетное значение d -критерия свидетельствует об отрицательной связи.

d `=1,75 и d 1 = 1,10, d 2 =1,54.

Так как расчетное значение критерия d больше верхнего табличного значения d 2 , то гипотеза о независимости уровней остаточной последовательности, то есть об отсутствии в ней автокорреляции принимается.

Вывод об адекватности модели делается, если все 4 проверки свойств остаточной последовательности дают положительный результат. Для адекватных моделей имеет смысл ставить задачу оценки их точности.

В качестве критерия точности мы принимаем степень совпадения теоретических и практических значений у .

Вычислим эти показатели:

Коэффициент детерминации - ϕ 2

R 2 = 1

при этом d -критерий меняется в пределах от 0 до 4.

Если d -критерий от 0 до 2, то это свидетельствует о положительной автокорреляции, а если в интервале от 2 до 4, то это свидетельствует об отрицательной связи.

В этом случае его надо преобразовать по формуле:

d`=4-d

и в дальнейшем использовать значение d`. Расчетное значение критерия d или d` сравнивается с верхним d 2 и нижним d 1 критическими значениями статистики Дарвина-Уотсона. Для 5 % уровня значимости эти значения для ряда количества определяемых параметром p приведены в таблице 10.

ⁿ ∑ ( y i - ^~ y i )² i = 1

n

∑ ( y_i - y )² i = 1

ϕ 2

Он показывает долю изменения результирующего признака, объясняемую изменением включенных в модель факторов.

На основании указанных показателей можно сделать выбор наиболее точной из нескольких адекватных моделей. Хотя может встретиться случай, когда по некоторому показателю более точна одна модель, а по-другому – другая модель.

В рассматриваемой задаче:

σ=42,06; ε от =5,23;φ 2 =0,017,R 2 =0,98.

Полученное значение R 2 =0,98 подтверждает достоверность наличия зависимости.

Согласно произведенным расчетам, мы нашли, что уравнение множественной регрессии имеет вид:

y=41,02+0,87x2+14,84x3.       (10)

Также мы провели анализ полученных результатов и убедились в том, что:

• -    наличие зависимости между X i и Y является достоверным;

• -    имеется сильная корреляционная зависимость между Y и Х i ;

• -    коэффициенты регрессии являются значимыми.

Таким образом, модель может быть признана адекватной. В целом данное уравнение можно использовать для определения расчетного значения пищевой и биологической ценности продукта, так как случайные ошибки коэффициентов будут взаимопогашаться.

При проверке свойств остаточной последовательности, которые были выделены существенными для исследуемого явления, было обнаружено:

• -    гипотеза о случайном характере отклонений уровней остаточной последовательности принимается;

• -    случайная компонента распределена по нормальному закону распределения;

• -    - гипотеза о равенстве нулю математического ожидания случайной последовательности принимается;

• -    - гипотеза о независимости уровней случайной компоненты (т.е. об отсутствии в ней автокорреляции) принимается.

Таким образом, остаточная последовательность удовлетворяет всем свойствам случайной компоненты временного ряда, следовательно, найденная нами линейная модель является адекватной.