Оценки модуля аналитической в прямолинейной полосе функции

DOI:

В теории функций комплексных переменных известны роль и значения различных оценок модуля аналитических функций внутри области, если известна соответствующая оценка на границе или части границы этой области. Такие оценки возникали при появлении стройной теории функций комплексных переменных. Для этого достаточно вспомнить историю возникновения гармонической меры в теории потенциала или известных теорем типа Фрагмена – Линделефа. Оценки подобного рода играют существенную роль в приложениях теорий функций комплексных переменных. Для примера вспомним теорему Рисса – Торина или теорему об аналитических емкостях. В 1966 г. в журнале «Математический сборник» Ю.И. Масляковым был опубликован результат об оценках модуля аналитических функций внутри правой полуплоскости при условии, что есть некоторая оценка убывания модуля функции на мнимой оси [4]. Оказалось, что оценки такого рода справедливы не только для аналитических непрерывных вплоть до границы и ограниченных функций, но и для функций из классов И.И. Привалова [5], где на границе оценка «всюду» заменяется на оценку «почти всюду» и существенно расширяется класс функций, где справедлив такой результат (см.: [2; 7]). Аналогичные оценки для модуля функций из классов И.И. Привалова можно получить не только в правой полуплоскости, но и в единичном круге [1], и в прямолинейной полосе [6].

Основной результат

<

π

Лемма 1. Пусть функцияfz) - аналитическая в прямолинейной полосе П = < x + iy: | y| тогда:

- x

π

+—

ln| f ( z )| < 2 r lim en J ln ⁺ | f ( x + iy )| dy +

π

где

П *

где

1 +l

+1J n -L

r = |z |, ln * a = <

I П I t x ln f I t + i — I e e cos ydt

t x          ²       2 x 2

( e - e sin y ) + e cos y

In a , при a >  1;

1 +L

+1J n -L

1 Г I • П

In f\t -i —

I 2

e^te^x cos ydt

( e + e x sin y ) + e ² x cos² y

0, при 0 <  a <  1.

Доказательство. Функция f ( w ) , аналитическая в правой полуплоскости

~

= { и + iv : и >  0 } , имеет оценку [2, с. 10]:

π +—

1       2                     _

lnl f(w X <2 r Rm nR J In * If(Re” I d6+

π

| w | = r .

u_ +L _ f |_ , П -L ( t - V ) 2 + _ ² ,

Так как -l <  t <  +l , то последний интеграл в (1) примет вид:

_M ^+L lnl f (i F)|         _M ^+L lnl f (- i f)|

^_ --- dt + ^{_ V} \ ) dt, t >  0 .

П ^J 0 ( t - v )² + и ²       П ^J ( t + v )² + и и

Конформно отобразим П+ = {u + iv: и > 0} на П = < x + iy: |y| < П I при помощи функции ln w = z.

Делая замену x = ln | w , y = arg w , и = e x cos y , v = e x sin y , R = e x , 6 = y , имеем:

^ln| ^f ( ^w )|= ^ln| ^f ( ^e z )| = ^ln| ^f ( z )| , ^ln| ^f ( ^{it r} )|= ^{ln f} [ ^ln t l ± ⁱ 2_

Пусть t = ln |?|, t > 0.

Из (3) получим dt = edt , -l <  t <  +l .

Учитывая (2) и делая замену в (1), имеем:

- x

π

+—

ln| f ( z )| < 2 r lim — j ln ⁺| f ( x + iy )| dy + x .. ⁿ n

+L

+ 1

ⁿ -L (

I      П ln f t + i —

[     2

e^te^x cos ydt

।      П ln f t - i —

[     2

e^te^x cos ydt

tx     ² 2 x 2

e - e sin y ) + e cos y

+L

+ 1 f t x          2      2x     2

ⁿ -l ( e + e sin y ) + e cos y

Лемма доказана.

^{n 1}

X + iy : । y | < — >  функций f ( z ), удовлетворяющих условию:

I +X                                          I

1) . ^sup , 1

—< y <+— 22

X

p

;

π

+—

• - x 2

• 2) lim— J /n ⁺| f ( x + iy )| dy = 0 .

x ^п П

Такой класс функций называют классом И.И. Привалова в прямолинейной полосе.

Лемма 2. Если функция f ( z ) е N p ( П ) , то

1 +X

lnlf (Ф^Ё π

^{-x (}

1 r I ,    • П ln f t + i —

I 2

e^te^x cos ydt

।      П ln f t - i —

I     2

e^te^x cos ydt

t x          ²       2 x     2

e - e sin y ) + e cos y

-| +X

+1 f              2           , t x          2      2x 2

ⁿ x ( e + e sin y ) + e cos y

I                    П I при всех z е П = 1 x + iy : |y| < — >.

Доказательство. По лемме 1 функция ln | f ( z )| имеет оценку:

π + - x 2

ln | f ( z )| <  2 r lim - — j ln ⁺ | f ( x + iy )| dy + x ^” ^п П

-| +X п -Ц

1 r I .    • П ln f t + i —

I 2

e^te^x cos ydt

।      П ln f t - i —

I     2

e^te^x cos ydt

t x          ²       2 x     2

e - e sin y ) + e cos y

-| +X

+—                 .2             .

t x          ²       2 x 2

ⁿ x ( e + e sin y ) + e cos y

Так как f ( z ) е N p ( П ) , то

π

+—

- x 2

lim— f /n ⁺| f ( x + iy )| dy = 0 .

x ^x 77- J ।   ^        ^

ππ

В результате справедливо следующее неравенство:

1 +X ^lnl ^f ( z )l<- 1 ⁿ -X

I П l ln f I t + i — I e e cos ydt

t x          ²       2 x     2

( e - e sin y ) + e cos y

1 +X

⁺ П 1

1 r I • П ln f\ t - i —

I 2

e^te^x cos ydt

t x          ²       2 x     2

( e + e sin y ) + e cos y

.

Лемма доказана.

Обозначим через В класс положительных, возрастающих, непрерывных функций ф ( 1 ) на [ 0, +х ) , удовлетворяющих условиям:

a) ф ( е* ) выпукла вниз при t >  0 ;

да

• b)    Jv( t) e-tdt < +да;

v( e)

• c)    lim —-—- = +да .

t ^+да t

Теорема 1. Пусть функция

^f ( ^z ) ^e N p ( П ) ,p >  1,

и на границе П почти всюду удовлетворяет условию

f

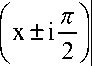
< e ^{ф ( Х )} , ( - да <  x <  + да ),

где ф ( t ) e B. Тогда всюду в П справедлива оценка

|f ( z )| < K e ^{z )} , K= e^{ф ( 1 )- ф ( 0 )}.

Доказательство. По лемме 2

+да

lnl f(z ^-f π

-да

1 r I ,    • П ln f\t + z —

I 2

e^te^x cos ydt

( e - e^x sin y ) + e ^{2 x} cos² y

1 +да

+-4 π

-да

1 Г I • П ln f t - z —

I 2

e^te^x cos ydt

( e t + e x sin y ) + e ^{2 x} cos² y

Из условия (4) получим:

^ln| f ^{( z} )| < ^-

1 ^+да ф ( I t ) e t e x cos ydt 1 ^+да ф ( I t ) e t e x cos ydt ^п -да ( e t - e^x sin y ) + e^{1 x} cos² y ^п -да ( e t + e^x sin y ) + e ^{2 x} cos² y

1 +да ф ( It ) etex cos ydt 1 +да ф ( 11 ) etex cos ydt п -да( et - ex sin y) + e2xcos2y п -да( et + ex sin y) + e2xcos2y

1 +да     ф (t) etex cos ydt        1 +да     ф (t) etex cos ydt п о (et - ex sin y) + e2xcos2y п о (e~t - ex sin y) + e1 xcos2y

1 +да     ф (t) etex cos ydt        1 +да     ф (t) etex cos ydt t x          2      2 x     2                  -1 x          2      2 x 2

^п о ( e + e sin y ) + e cos y ^п о ( e + e sin y ) + e cos y

Рассмотрим функцию

m ( 5 ) =

ts

max t>1 eV(t) .

Функция m ( 5 ) определена при всех 5 >  0, так как для таких 5 , в силу условий, наложенных на функцию ф , существует

In m (5) = max (5 In t - 9(t)) = max ( st - 9(eT)), v '       t>1 x                v           т>0 \           \ где In m (s) является функцией, двойственной по Юнгу к функции 9 (eT) [3, с. 186].

Заметим также, что функция m(s) - возрастающая при s > 0 и m (0 ) = e-9(1).

По функции m ( s ) построим функцию Карлемана – Островского:

Г ( t ) =

t^s max . s > ⁰ m ( s )

Функция Т(t) существует для любого t > 1, так как существует ln Г (t) = max (s ln t - In m (s)).

Функция In Г ( e ^T ) - двойственная по Юнгу к функции ln m ( s ), поэтому In Г ( t ) существует для всех t >  1 [3, с. 186].

Рассмотрим случай, когда 0 < t < 1. При этих значениях функция Т(t) тоже определена, так ts1

как в этом случае с ростом s функция —— убывает, следовательно, Г ( t ) = ——— (0 <  t <  1) .

m (s)

Учитывая соотношение (6), имеем

Г (t) = e9(1),0 < t < 1

Принимая во внимание, что 9 ( e ^T ) выпукла вниз, получаем [3, с. 187]

ф( eT )= ln Г (ет), т > 0, откуда e9 (t) - Г (t), t > 1.

Рассмотрим отрезок 0 < t < 1. В силу (7) и условий, наложенных на ф(t), справедливо соотношение e9 (t )< e9 (1) = Г (t).

Также для этого отрезка верно неравенство e9(t) > e9(0), откуда e9(t) > e ( )в ° = e9(о)-9(1)Г (t) = K 1Г (t), к1 = e9(°)-9(1).(9)

e ^{9 ( 1 )}

Замечая, что K1 < 1, и учитывая (8) и (9), имеем e9(t)> K1Г (t), t > 0.(10)

Пусть s0 – неотрицательное число, такое, что rs0

=Г ( r ).(11)

m ( s 0 )

Оценим интегралы, стоящие в правой части неравенства (5).

Из соотношений (10) и (11) получаем:

^lnl f ⁽ - ⁾l <^-

1 +^

+ π 0

—

π

1 +^

77 J

π ₀

ln K i

V

t s 0

A

¹ m ( s 0 ) ,

e^te^x cos ydt

( e - e^x sin y ) + e ^{2 x} cos² y

+^ + if π ₀

ln K 1

V

t

m ( s 0 )J

e t e^x cos ydt

( e* - e^x sin y ) + e ^{2 x} cos² y

+

f

In K 1

V

t)

m(s0)J

e^te^x cos ydt

( e t + e^x sin y ) + e ^{2 x} cos² y

+^

+if

77 J

π ₀

f ln K1

V

t

m ( s 0 )J

e t e^x cos ydt

( e ¹ + e^x sin y ) + e ^{2 x} cos² y

+»

J

ln ^{K 1} e^t e^x cos ydt

m (s 0)

( e t

- e^x sin y ) + e ^{2 x} cos² y

+w

+if

IT J

π ₀

ln K ¹ e t e^x cos ydt m ( s 0 )

( e -

- e^x sin y ) + e ^{2 x} cos² y

+

1 +»

+ ¹

IT *

ln

¹ e^te^x cos ydt

m (s 0)

^п о ( e t + e^x sin y ) + e ^{2 x} cos² y

+w

+If-n J0 (

ln

¹ . e t e^x cos ydt m ( s 0 )                 ₊

e t + e^x sin y ) + e ^{2 x} cos² y

+w

+ n J0 (

et

s ₀ ln te^te^x cos ydt

- e^x sin y ) + e ^{2 x} cos² y

+w

+if-n 0 (e

t

s ₀ In te t e^x cos ydt      +

- e^x sin y ) + e ^{2 x} cos² y

+

+w tx     22x2

ⁿ 0 ( e + e sin y ) + e cos y

s ₀ ln te^te^x cos ydt

+w

+if-п 0 (e

— t

s 0 In te t e^x cos ydt

+ e^x sin y ) + e ^{2 x} cos² y '

Полученные 8 интегралов обозначим через I i , i = 1,8 .

+^

I 1 = if 77 π ₀

ln ^{K 1} e^te^x cos ydt ln m ( s 0 )               _

( e t - e^x sin y ) + e ^{2 x} cos² y

K 1

m ( s 0 )

π

+^

J

d

f t X _ • A

™n y

V e^x cos y J

ft X ' e - e sin y

1      K 1

= ln n   m (s 0)

arctg

X _ • A

V e cos y J

+x

= -ln π

K 1

V

n

m ( s 0 ) V ²

—

X.

e cos y J

arctg

+ 1

f 1 - e^x sin y

V e cos y JJ

.

Учитывая, что интегралы 1 ₂, 1 3 , 1 4 вычисляются аналогично 1 1 и arctg ( t ) - функция нечетная, получим:

1 K 1

¹ 1 ^{+ 1} 2 ^{+ 1} 3 ^{+ 1} 4 = ^ln /  \

n   m (s 0)

π

—

arctg

C A X • A l- x ^in, ,

V e cos y J

+ arctg

e ^^in y

V e cos y J

+ arctg

C A X • A i- x^y

V e cos y J

+

+

π

arctg

Гл . х ■ Л

1У^

V e cos У )

—

arctg

Г X ■ л in

V e cos У )

+ arctg

1У^

V e cos У )

= In K 1 — In m ( 5 0 ) .

Найдем оставшиеся четыре интеграла. Пусть

ˆ

I — Is + I a + I"i + 1 % .

Рассмотрим функцию f ( 2, у) — In

2 2 +

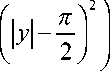
— In ^f Г + y ²

V

— П

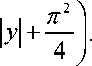
Это гармоническая функция в П —

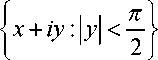
так как:

5 f ( x , у ) = 2 x         бf ( x , у ) _—      2 у + п

5 2        ₂    7 —      п ^{2 ,}     5 у        ₂    2 - п ²

2 + у + п у + —        2 + у + п у + —

г

⁵ 2 ^f ( ² , У )

„  22-

^{2 2} + у ^{+ п} у + —

V4_ f-' У

2 ² + у ^{2 +} п у + ~

V

—

4 x ²

)

⁵ 2 ^f ( ² , У )

5 у У

тт² ^

2 22 + у2 + п у + —

V 4 )

— ( 2 у + п ) ²

22 + у2 + п у + ~

V              4 )

5 ² f ( 2 , у ) 5 ² f ( 2 , у ) _ 4 2 ² + 4 у ² + 4 пу + п ² 4 2 ² — 4 у ² ± 4 пу

5 2 ^{2     +}   5 у ^{2    —            :}                 ~

г

V

2 V

2 ² + у ² + пу + ~

⁴ )

—

п — 0

.

На границе полосы П — 1 2 + iy : | у | <  ^п^ ln ( t ² + 0) — 2 ln 1 1 1 .

функция f ( 2 , у ) — ln

2 ² +

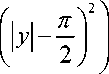
равна

Представим функцию

ln ^f 2 ² + У ²

V

— п| У + п

⁴ )

где r — 2 + у , че-

s рез ядро Пуассона, предварительно умножив на 0 :

^{5 0} ln r²

2 V

— п| У + п

1 +?     50ln |t|ete2 cos ydt п —»( et — e2 sin у) + e22 cos2 у

+^

+У π

—да

s ₀ ln t e^te^x cos ydt

( e t + e² sin у ) + e ^{2 2} cos² у

1 ⁺ ?      5 ₀ ln tee² cos ydt       1 У      5 ₀ ln te*e² cos ydt

= 77 * ( t 2         \² . 2 2     2                   — t     2         \² . 2 2     2

^п о ( e — e sin у ) + e cos у ^п о ( e — e sin у ) + e cos у

1 ⁺ ?      5 ₀ln tee² cos ydt 1 У      5 ₀ln te t e² cos ydt

ˆ

^— I 5 ⁺ I 6 ⁺ I 7 ⁺ I 8 ^— I

t 2          ²       2 2     2                   — t      2          ²       2 2     2

^п о ( e + e sin у ) + e cos у ^п о ( e + e sin у ) + e cos у

Так как ln|f ( z)| - "" [11 + I2 + I3 + I4 + I"\ ,

МАТЕМАТИКА И МЕХАНИКА то ln|f ( z )|< —

ln K ₁

- In m ( 5 0 ) + In

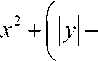
π

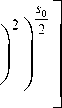
В силу справедливости неравенства s0 ln

x ² +

к

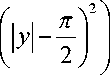
> — In x ² + 2

к

π

—

π

2)7

= In | x|⁵⁽

получаем:

ln| f ( z)|< —

In K 1 + In

r^{s 0}

m (5 о)

откуда следует неравенство Теорема доказана.

If ( z )| < K e^^z, K= е^{ф ( 1 )— ф ( 0 )}.