On collectively-Levi sets of operators

Several kinds of Levi operators were studied recently in [1–4] The present paper concerns collective properties of σ-Levi operators.

In what follows, vector spaces are real and operators are linear. The letters E and F stand for vector lattices, symbols L(E, F), L fr ( E, F), and K(E, F) for the spaces of linear, finite rank, and compact operators from E to F , B X for the closed unit ball of X, and I X for the identity operator in X. We write y n | 0, whenever y n ‘ C y n for all n ‘ ^ n and inf e y n = 0.

Throughout the paper, we say that a sequence (x n ) in E is order convergent to x G E (briefly, x n — x) if there exists a sequence (p n ) in E, p n ^ 0 such that | x _n — x | C p n holds for all n. A sequence (x n ) in E is order Cauchy if, for some p n | 0 in E, | x _n ‘ — x n ’’ | C p n

• ^# The research was carried out within the framework of the state contract of the Sobolev Institute of Mathematics, project № FWNF-2022-0004.

whenever n',n" ^ n. A vector lattice E is said to be sequentially order complete whenever each order Cauchy sequence in E is order convergent.

The following definition is an adopted version of [1, Definition 1.1] and [3, Definition 1].

Definition 1. An operator T from a normed lattice E to a vector lattice F is:

• a)    a-Levi if, for every increasing bounded sequence (x n ) in E ₊ , there exists x G E with Tx n — Tx. The set of such operators is denoted by L L_evi (E, F ).

• b)    quasi-c-a-Levi if, for every increasing bounded sequence (x n ) in E ₊ , the sequence (Tx n ) is order convergent. The set of such operators is denoted by L qcLevi (E,F ).

• c)    quasi-a-Levi if, for every increasing bounded sequence (x n ) in E ₊ , the sequence (Tx n ) is order Cauchy. The set of such operators is denoted by L qLevi (E, F ).

Clearly, L Le_vi (E,F ) C L "_cLe_vi (E,F) C L^ ev (E,F ). The following example shows that both inclusions are proper in general (cf., [2, Example 1]).

Example 1. First we show that the inclusion L L_evi (E) C L qcLevi (E) can be proper. Define an operator T on E = C [0,1] ® L i [0,1], by T((ф, 0)) := (0, ф) for ф G C [0,1] and -0 G L i [0,1]. Clearly, T G L q_cLevi+ (E). Consider ф _п G C [0,1] that equals to 1 on [0, 2 — ^n] , to 0 on [^ , 1], and is linear otherwise. Let f n := (ф _п , 0). Then (f _n ) is bounded and increasing in E ₊ , and Tf n — (0, g), where g G L i [0,1] is the indicator function of [0, |] . Since g G C [0,1], there is no such an f G E that Tf = (0, g), and hence T / L £_evi (E).

For the second inclusion, consider the Banach lattice c of convergent real sequences and denote elements of c by ^^ =i a n • e _n , where e n is the n-th unit vector of c and (a n ) converges in R. Since each bounded increasing sequence in c ₊ is o-Cauchy, I _c G L qLevi (c). However, a bounded increasing sequence I _c f _n = f n := П =_{к = 1} e 2 k - i in c + is not order convergent. Thus, I c / L qcLevi (c).

We shall use the following Lemma (cf., [2, Lemmas 1, 2]).

Lemma 1. Let E be a normed lattice and let F be a vector lattice. The following holds.

• i)    L qcLevi (E, F) and L qLevi (E, F) are vector spaces.

• ii)    L fr ( E,F ) C LL vi (E,F) .

• iii)    If F is a normed lattice then K ₊ (E, F ) C L qcLevi (E, F ) •

• <1 i) It is trivial.

• ii)    Let T G L fr (E, F ), say T = £ n _=i f _k 0 y _k for y i ,...,y n G T (E) and f i ,...,f n G E'. Denote

nn

T i := Ef + ⁰ У ^к , T 2 := Ef - ⁰ У к • k =i                  k =i

Let (x _m ) be an increasing bounded sequence in E ₊ . Then, for each k, the sequences f + x m ) and f ^— (x m ) are increasing and bounded. Thus, f + (x _m ) — a k and f ^— (x m ) — b k for some a k ,b k G R ₊ . Since dim(T(E)) <  от ,

T i x m — E a k y k G T(E), T 2 x m — 52 b k y k G T(E). k =i                           k =i

Therefore,

Tx m = (T i x m — T 2 x m ) — E^ k - b k )Ук G T(E). k =i

Take an x G E, such that Tx = ^ n =i (a k — b k )y k . Then Tx m — Tx. We conclude T G L Levi (E,F ).

• iii)    Let T G K ₊ (E, F) and let (x m ) be an increasing sequence in ( B e ) ₊ . Then (Tx m ) has a subsequence (Tx m j ) satisfying ^ Tx m j — y || 4 0 for some y G F . Since Tx m t then \ Tx m - y | 4 0. As each norm convergent increasing sequence converges in order to the same limit then Tx m —> y, and consequently T G L g_cLevi (E,F). >

The next example strengthens Example 1 by showing that the inclusion L £_ev (E) И K + (E) ^ L qcLevi (E) И K + (E) can be proper (cf., [2, Example 2]).

Example 2. Let (a n ) be a vanishing real sequence consisting of non-zero positive terms. Define an operator S from c to c o by S (£ “ ₌₁ a n e n ) = J2^ ₌₁ (a _n a _n )e _n . Then S G K ₊ (c, c o ), and hence S G L qcLevi (c, c o ) by Lemma 1. Take a bounded increasing sequence x n = J2n ₌ i e 2 k in c ₊ . The sequence (Sx _n ) = (5Zn ₌₁ a ₂k e ₂ k) converges in order to £^1 a ₂ k e ₂ k G co, however there is no x G c with Sx = £j” i a 2 k e 2 k • Indeed, would such x = £j” i a k e k G c with Sx = S( ^2k =i a k e k) = Y =k a 2 a 2 k e 2 k exist, it must satisfies a k = 1 for even k-th and a k = 0 for odd k-th, which is absurd. Therefore, S / L £_evi (c, c o ).

The operator S is also a counter-example to [1, Proposition 3.5].

Now, define a sequence (S i ) of operators in L fr ( c, c o ) by S i (^“ =i a n e n ) = ^ i_n =i (a n a n )e n - Trivially, S i — S . By Lemma 1, S i G LL^c, c o ). Since S / LL^c, c o ) then the set L [_evi (c, c o ) is not closed under the operator norm.

It is worth noting that, generally, L ^ev (E, F ) need not to be a vector space [2, Example 8].

The present paper is organized as follows. Section 2 is devoted to elementary properties of collective order convergence of families of sequences. Section 3 is devoted to collectively σ -Levi sets of operators, their relations to collectively compact sets, and for the domination problem.

For unexplained terminology and notation we refer to [5–8].

2.    Collective Order Convergence

Working with families of sequences of elements of a vector lattice requires a certain notion of “collective” order convergence. In what follows, we identify E -valued sequences and elements of the vector lattice E ^N equipped with the pointwise linear and lattice operations.

Definition 2. Let A ⊆ E ^N . We say that A collective order converges to an indexed subset { c _a } _ae A of E (briefly, A c-o { c _a } _ae A ) whenever there exists a sequence (p _n ) in E, p _n ^ 0 such that | a _n — c a | C p n holds for all n and all (a n ) G A . We call A collective order-null if A ч { 0 } _ae A .

In this section we give some elementary properties of collective order convergence which are used in Section 3. The following proposition is elementary and its proof is left to the reader.

Proposition 1. Let A and B be nonempty collective order convergent subsets of E ^N , and let α, β ∈ R . The following sets are collective order convergent.

• i)    A ∪ B .

• ii)    aA + вВ := { (aa n + eb n ) } a e A ; b e B •

• iii)    | A I := { ( | a n | ) } a e A •

• iv)    The convex hull co(A ) of A in E N •

Moreover, v) If A 4 { c a } _{a E} A and A 4 { c^^ A then c a = c' a for all a G A .

• ^{vi)    A 4 { c} a ^} a e A ^{iff { ( a} n ^{— c} a ^{) }} a e A ^{4 { 0 }} a e A •

• vii)    A sequence (a n ) in E order converges iff the set { (a n ) } is collective order convergent.

Note that the passing to solid hull does not preserve collective order convergence for any nontrivial E. Indeed, let 0 = x G E. Then the set A = {(an) : an = x} of one constantly x sequence is collective order convergent, yet its solid hull sol(A) is not, as sol(A)

(1+^ x)

contains a sequence

that does not order converge. It should be clear that if E is an Archimedean vector lattice then, for each order convergent to zero sequence (an) in E possessing at least one non-zero term, the set {(Aan) : A G R} is not collective order-null. Also, it is worth noting that the set {(^П)n : k G N} consisting of order-null real sequences is not collective order-null.

The next theorem extends items ii) and iv) of Proposition 1 to the Banach lattice setting as follows.

Theorem 1. Let E be a Banach lattice, let (p i,n ) _n be sequences in B e satisfying p in | 0 for each i G N , and let A i be nonempty subsets of E N such that | a i,_n | C P in holds for all i,n G N , and (a i,n ) _n G A i . Then, the set

∞

£ aiA = i=1

∞

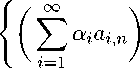
(a i,n ) n G A i , £|a i | C 1 i =i           J

is collective order-null. In particular, for every M >  0 and A f-° { 0 } a _e A in E N the set

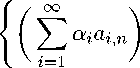
( a i_,n ) _n G A,

∞

E

i =1

| a i | C M

is collective order-null.

<1 Passing to the norm-limit as m ^ от in the following inequality

m

αiai,n i=1

m        m ∞

C £ | a i || a i,n | C £ l a i [ p in C £ | a i | p i,n , i =1                i =1              i =1

where (a i,n ) n G A i , we obtain (£“ 1 a i a in \ C P n := £“ 1 \ a i [ pi n for all n. Clearly, (p n ) is decreasing. It remains to proof p _n ^ 0. Suppose in contrary 0 < a C P n for all n. Fix an arbitrary m G N. Since 0 < a C ^2^ =1 | a i | p i,_n + ^2° = _{m +1} | a i | p i,_n for all n, and since inf _n ^ N £ i =1 \ ^a i ^{| p} i,n — ⁰, ^we obtain that ⁰ < a ^C £ i = _m +i \ ^a i ^|p i,n ^{for al}l ^m^{,n G} N. Therefore,

∞

∞

0 < ||a|| C limsup m →∞

|αi |pi,n i=m+1

C

lim m →∞

E

i = m +1

| a i | — 0,

which is absurd.

The rest of proof follows from the previous part by taking A i — A for all i G N. >

We finish this section with the following notion of collective order Cauchy set of sequences.

Definition 3. A set A C E N is collective order Cauchy if, for some p _n ^ 0 in E , | a _n ‘ — a n ’’ | C p _n holds for all a G A whenever n ‘ ,n ’’ ^ n. A vector lattice E is sequentially collective order complete if each collective order Cauchy subset of E ^N is collective order convergent.

The next elementary proposition shows that the sequential collective order completeness agrees with sequential order completeness.

Proposition 2. Let E be a vector lattice. The following conditions are equivalent.

• i)    If a sequence (x_n) in E satisfies \x_n‘ — x_n’’ | C p_n, whenever n,n‘ ^ n for some p_n ^ 0 in E, then there exists x G E with |x_n— x\ C p_nfor all n.

• ii)    If a subset A of EN satisfies |an‘ — an’’ | C pn for all a G A and some p_n ^ 0 in E, whenever n‘, n" ^ n, then there exists an indexed subset {ca}_aea of E, such that |an — c_a| C pn holds for all n and all (an) G A.

• iii)    E is sequentially collective order complete.

• iv)    E is sequentially order complete.

3.    Collectively σ-Levi Sets of Operators

< Implicationsi)^ ii)^ iii)^ iv) are trivial.

iv)^ i) Let | x _n ‘ — x _n ’’ | C p n for all n ‘ , n " ^ n and some p _n ^ 0 in E. Since E is sequentially order complete, x _n — x for some x G E. Sending n " — ж and passing to the order limit in the inequality | x _n — x _n ’’ | C p n , where n ’’ ^ n, we obtain | x _n — x | C p n for all n. >

Recall that a set A of operators between normed spaces X and Y is collectively compact whenever Ut ^ a T ( B x ) is relatively compact in Y [6]. This section is devoted to collectively σ -Levi sets of operators, their relation to collectively compact sets, and the domination problem for collectively σ -Levi sets. We begin with the following collective version of Definition 1.

Definition 4. Let E be a normed lattice, F a vector lattice, and A C L(E,F ). We say that A is:

• a)    a collectively a-Levi set if, for every increasing bounded (x _n ) in E ₊ , there exists an indexed subset { x t } t ^ a of E satisfying { (Tx n ) : T G A } — { Tx t } t _e A .

• b)    a collectively quasi-c-a-Levi set if, for every increasing bounded (x n ) in E ₊ , there exists an indexed subset { у т } t ^ a of F satisfying { (Tx n ) : T G A } — { у т } t ^ a .

• c)    a collectively quasi-a-Levi set if, for every increasing bounded (x n ) in E ₊ , the set { (Tx n ) : T G A } C F N is collective order Cauchy.

Obviously, T lies in L £_evi (E, F ) (L qcLevi (E, F ), L qLevi (E, F )) iff the set { T } is a collectively a-Levi (resp., collectively quasi-c-a-Levi, collectively quasi-a-Levi) subset of L(E, F).

We continue with the question on which properties of σ -Levi, quasi-c- σ -Levi, and quasi- σ -Levi operators mentioned in Lemma 1 have collective versions. The properties described in Lemma 1 i) have the following extension.

Proposition 3. Let E be a normed lattice, F a vector lattice, and A,B C L(E,F). The following holds.

• i)    If A and B are both collectively quasi-c-a-Levi then the set { aT + eS : | a | + | в | C 1, T G A, S G B } is also collectively quasi-c-a-Levi.

• ii)    If A and B are both collectively quasi-a-Levi then the set { aT + eS : | a | + | в | C 1, T G A, S G B } is also collectively quasi-a-Levi.

• <1    i) By the assumption, there exist sequences p n ^ 0, q _n ^ 0 in F , and indexed subsets { у т } т e A , { z s } s e B of F satisfying | Tx n — у т | C p n , | Sx n — z s | C q n for all T G A, S G B , and n ∈ N. The result follows from

| (aT + eS')x n ~ ( ау т + ez s ) | C | a | p n + | в | q n C (p n + q n ) I 0.

• ii)    Let sequences (p n ), (q _n ) in F satisfy | Tx _n ‘ — Tx_n ’’ | C p n I 0 and | Sx _n ‘ — Sx _n " | C q _n I 0 for all T G A, S G B, and n' ,n " ^ n. The result follows from

| (aT + eS)xn‘ - (aT + eS)xn’’)| C (pn + qn) I 0, for n', n" ^ n. >

The items ii) and iii) of Lemma 1 have no reasonable collective extension. To see this, define norm-one functionals T k on c g by T k a = a k . Thus, T k G L fr ( c q , R), yet the set { T k } k _E N is not even collectively quasi-a-Levi. Indeed, for the increasing bounded sequence x n = £m ₌₁ e m in c g , there is no sequence p n ^ 0 in R with [ T k x n ‘ — T k x n ’’ | C p n for all k and n ,n " ^ n, since | T n +i x n — T n +i x n +i | = 1 for every n. Moreover, { T k } k _E N is a collectively compact subset of L ₊ (c o , R) that is not collectively quasi-a-Levi.

Now, we apply Theorem 1 for strengthening Proposition 3 in the Banach lattice setting as follows.

Theorem 2. Let E be a normed lattice, F a Banach lattice, and let A be a bounded collectively quasi-c-a-Levi subset of L(E,F). Then the set

∞

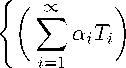
Ti G A, £^i| с И i=1          J

is collectively quasi-c-a-Levi, where ^“ i a i T i is the limit of partial sums ^[=1 a i T i in the operator norm.

< Let (x n ) t in ( B e ) ₊ . Then { (Tx n ) } t . a — o { у т } t . a for some subset { у т } t . a of F . Proposition 1 vi) gives { (Tx n — у т ) } т _e a -— { 0 } t _e a . By Theorem 1,

∞

^ a i (Tx n — i =i

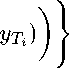
T i ∈ A, ∞

E | ai IC 1

i =1

c-o ^{{ 0 }} TE A, ■ ∞

E | ai |C 1

i =1

So, there exists a sequence p _n ^ 0 in F satisfying

VaA

αi i xn i=1

∞

— £ ai yTi i=1

∞

^2 a i (T i x n — y T i )

i =1

C P n

for all n, T i G A, and all a i with £“ 1 | a i | C 1, where the series £“ 1 a i T i converges in the operator norm due to boundedness of A. The proof is complete. >

Since every Dedekind σ -complete vector lattice is sequentially order complete, the next corollary follows from Proposition 2 and Theorem 2.

Corollary 1. Let E be a normed lattice, F be a Dedekind σ-complete Banach lattice, and A be a bounded collectively quasi-a-Levi subset of L(E,F). Then the set

{(E a‘ T^ : Ti G A f>K 1} is collectively quasi-c-σ-Levi.

Now, we discuss of the “collective” domination problem for Levi sets of operators. First, recall some already known related results for Levi operators.

The quasi- σ -Levi operators do satisfy the domination property (cf. [1, Theorem 2.7], [3, Theorem 3]). We do not know where quasi-c- σ -Levi operators satisfy the domination property. In general, σ -Levi operators do not satisfy the domination property (cf. [2, Example 7]).

Example 3. Define operators S,T G L(c) by

S

(““

E *■ en = Ean en ; T n=1

(“     \    “ / “\

E a n e n = EE a k n =1          n =1 k =1

e n ^.

Then 0 C S C T . Operator T has rank one, and hence T is a-Levi by Lemma 1 ii). However, S / L b_evi (c) due to Example 2.

We use the following “collective” notion of domination for sets of operators.

Definition 5. Let A, B C L + (E, F ). Then A is dominated by B if, for each S E A, there exists T E B with S C T •

We conclude the paper with the following “collective” partial generalization of [1, Theorem 2.7] in the class of quasi- σ -Levi operators.

Theorem 3. Let E be a normed lattice, F be a vector lattice, and A,C C L + (E,F) be such that A is dominated by C . If C is collectively quasi-σ-Levi then A is also collectively quasi-σ-Levi.

<1 Let (x _n ) be an increasing sequence in ( B e ) + . By the assumption, C is collectively quasi-a-Levi, and hence the set { (Tx n ) : T E C } C F N is collective order Cauchy. By Definition 3, for some p _n ^ 0 in F , | Tx _n ‘ — TX _n ’’ | C p n holds for all T E C whenever n', n" ^ n.

Let S E A. Then 0 C S C T s for some T s E C . Since | T s x _n ‘ — T s x n ’’ | C p n for n ' , n" ^ n,

| Sx n ‘ — Sx n ’’ | C | Sx n ‘ — Sx n | + | SX n ’’ — Sx n |

= S(x n ‘ — X n ) + S(X n ’’ — X n ) C T s (x n ‘ — X n ) + T s (x n ’’ — X n )

= ITsXn’ — TsXnl + ITSXn’’ — TsXnl C 2pn for all n', n" ^ n. Because S E A is arbitrary and 2pn ^ 0, we conclude that A is collectively quasi-a-Levi. >