On generalized Kenmotsu manifolds as hypersurfaces of Vaisman-Gray manifolds

In 1972, K. Kenmotsu introduced a new class of almost contact metric manifolds [1]. In 2002, S. V. Umnova [2] introduced a generalization of Kenmotsu manifolds that studied later by I. K. Erken et al. [3] and N. Heidari et al. [4] under the title nearly Kenmotsu manifolds. Whereas, A. Abu-Saleem and A. R. Rustanov [5] investigated some curvature identities of a special subclass of that class introduced by S. V. Umnova [2]. Additionally, H. M. Abood and M. Y. Abass [6] constructed a new manifold which is a generalization of Kenmotsu manifold and they called it a manifold of Kenmotsu type.

On the other hand, M. B. Banaru and V. F. Kirichenko [7] focused on the hypersurfaces of almost Hermitian manifolds that have almost contact metric structures. They also derived the complete first group of Cartan’s structure equations. Continued in the same way, L. V. Stepanova et al. [8] discussed the hypersurfaces of the K¨ahlerian manifolds that have quasi-Sasakian structure. Moreover, M. B. Banaru and G. A. Banaru [9] demonstrated that a minimal hypersurfaces of a K¨ahlerian manifold, equipped with an almost contact metric Kirichenko–Uskorev structure that found in [10], is totally umbilical if and only if it is totally

geodesic. Also, M. B. Banaru et al. [11] showed that 2-hypersurfaces and 3-hypersurfaces of the almost Hermitian manifolds of class W 4 admit almost contact metric structures.

Therefore, in this article, we studied the hypersurfaces of Vaisman–Gray manifold which equipped with generalized Kenmotsu structure in Section 3, after the preliminaries in Section 2.

2.    Preliminaries

We symbolize by M n a smooth manifold M of dimension n and X ( M ) is the Lie algebra of smooth vector fields over M .

Definition 1 [12]. An almost contact metric manifold (shortly, AC M -manifold) is the smooth manifold M ²ⁿ⁺1 equipped with the quadruple (Ф,£,п, g) , where Ф is a (1,1) -tensor, £ G X ( M ) , n is the dual of £ , and g is the Riemannian metric such that the following conditions hold:

Ф( £ ) = 0, n ( £ ) = 1, n ◦ Ф = о, Ф 2 = - id + n 0 £, д(ФХ, ФY) = g ( X, Y ) - n ( X ) n ( Y ) ( V X,Y G X ( M )) .

Definition 2 [13]. An almost Hermitian manifold (shortly, AH -manifold) is the smooth manifold N ^2m equipped with the pair ( J, h ), where J is a (1, 1)-tensor and h is the Riemannian metric such that the following hold:

J ² = - id , h ( JX, JY ) = h ( X, Y ) ( V X,Y G X ( N )) .

Definition 3 [14]. A generalized Kenmotsu manifold (shortly, GK -manifold) is an ACM -manifold ( M ²ⁿ⁺1 , Ф ,£,п,д ) which satisfies the following identity:

Vx(Ф)Y + Vy(Ф)X = -n(Y)ФX - n(X)ФY (VX,Y G X(M)), where V is the Riemannian connection (i. e. Levi-Civita connection) of the metric g on M. On the other hand, the ACM-manifold (M2n+1, Ф, £, n, д') becomes Kenmotsu manifold if the above identity reduces to the following:

V x (Ф)Y = - g ( X, ФY ) £ - n ( Y )ФX ( V X, Y G X ( M )) .

Definition 4 [13]. A Vaisman–Gray manifold (shortly, V G -manifold) is an AH -manifold ( N ^{2 m} , J, h ) which satisfies the following identity:

V x ( F )( X,Y ) = -    ¹    {h ( X,X ) 6F ( Y ) - h ( X,Y ) 6F ( X ) - h ( JX,Y ) 6F ( JX )}

2( m - 1)

(VX,Y G X(N)), where F(X,Y) = h(JX,Y), 6 is the codifferential operator and V is the Riemannian connection (i. e. Levi-Civita connection) on N .

Remark 1. The method of associated G -structure (briefly, AG -structure) space introduced by V. F. Kirichenko [15] and used by A. R. Rustanov et al. [16] in Russian version and exists in [5] as an English translation. So, the authors can learn more about this method from these citations. Also, we summarize the AG -structure space of AC M -manifold ( M ^{2 n +1} , Ф ,£,д,д ) as follow:

Suppose that { / = e g , e i ,..., e n , Ф(е 1 ),..., Ф(е _п ) } is an orthonormal basis of X(M) , then Kirichenko’s method produced another basis as

{€     E0,^1>•••>En,^1,•• • , En}, where

ε _a

= ^ 2 ( ^e a - V- l^e a );

^E a = ^ 2 (e a + V- l^e a ))

a = I, 2)...)П, a = a + n.

So, we get:

/1 0 0\               /0     0         0    \

( g ij ) = 0 O I n ,     (Ф ) ) = 0 V- 1 I n      O ,              (1)

\0 i n о)           \0    о   -V— 1 i n]

where I n is n x n identity matrix and i,j =0,1,..., 2n .

On the other hand, the AG -structure space of AH -manifold (N ^{2 m} , J,h) is summarized by [15]:

Suppose that { е 1 ,...,ё _т ,J (£ i ),..., J (e _m ) } is an orthonormal basis of X (N) , then

Kirichenko’s method produced another basis as { Ё 1 ,..., E m , Ёр ..., E m } , where

£ b =

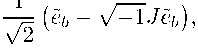
^E b =

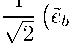
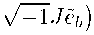
So, we get:

⁽h ki )=GO Io),   (J k )=(G? ^{I m} - On ),

\Im  O /              \ O v 1 Im/ where b = 1, 2,..., m, b = b + m, and k, l = 1, 2,... , 2m.

Theorem 1 [14] . The first group of Cartan’s structure equations of GK -manifold of dimension 2 n + 1 on the AG-structure space is given as the following:

• 1)    dw = F ab w a Л w ^b + F ^ab w a Л w b ;

• 2)    dw a = w a Л w ^b + C ^abc ш ь Л w c + 2 F ^ab ш ь Л w - 5 a w ^b Л w;

• 3)    dw a = — w a Л w b + C abc w b Л w c + 2 F ab w b Л w — ^ a w b Л w , where

Fab = V—1 Ф0 H  Fab + Fba = 0,  Cabc =    1 Фa., a,b                        ’                 2 b,c

F ab = -V- ^1ф a,b ⁾   F ab ^{+ F} ba = ⁰,   C abc =    2  ^{Ф a},c ⁾

C ^{[ abc ]} = C ^abc ,  C abc = C abc ,  C [abc] = C^  F ab = F ab ,

Ф } k are the components of V x (Ф)Y on the AG-structure space, [... ] is the anti-symmetric operator of their indices, a, b, c = 1, 2 ,...,n, а = a + n and C ^abc , F ^ab are the complex conjugate of C ^abc , F ^ab respectively.

Definition 5 [17]. The GK -manifold is called

• 1)    a special generalized Kenmotsu manifold of the first kind (briefly, SGK 1 -manifold) if abc

C  = C _ab_c = 0 ;

• 2)    a special generalized Kenmotsu manifold of the second kind (briefly, SGK 2 -manifold) if F ^ab = F ab = 0 ;

• 3)    a Kenmotsu manifold if C ^abc = C abc = 0 and F ^ab = F ab = 0 .

Theorem 2 [18] . The first group of Cartan’s structure equations of V G -manifold of dimension 2 m on the AG-structure space is given as the following:

• 1)    dw a = ^ a Л w ^b + B ab w ^c Л w _b + B^abc w _b Л w _c ;

• 2)    dw _a = - w a Л W b + B ab w _c Л w^b + B abc w ^b Л w ^c , where

B abe =V 1 j^, B [ abc ] = B ^abc , B ^abc = B abc ,  B abc = - J [b,c] ,

B[abc] = Babe, Bb = a^b], B? = «^b, Bab = Bab, a is the Lee form, Jj k are the components of Vx (J)Y on the AG-structure space and a,b,c = 1,2,... ,m, a = a + m.

Theorem 3 [7] . An ACM-manifold (M ^{2n - 1} , Ф,^,п, g) which is a hypersurface of an AH-manifold ( N ^{2 n} , J, h ) has the following first family of Cartan’s structure equations:

dw a = w a Л w^b + B C w ^e Л w b + B ^abe

w b л W c + (V2 Bbⁿ + У— 1 o a ) w^b л w

+

(T- T yb-— 2 B nab

-

B

..I

• ab

n

-

¹ vabnX    л

— = ^B   jw_b ^{Л w} ,

dw a

-wa л wb+Babw л wb+Babcwb л wC+(—2 Ban_ —-T °a) wb л w _ (—-1 °ab + —2 Bnab + —=1 Bn + у Bain) wb Л w, dw = V2 B-т wa Л wb ■ \ 2 Bnab w-a Л wb + Ш Bna - ^2 Bar - 2 V-raa} wb Л w^ nab                         a b           b           nb             b          a

+ (Bnl. + Bj +   ■ ani) w л wb + (Bnbn + Bn - 7-1 on) w Л wb, where

B[ab]   abab    r>c _         Йabc       1 ja     v _        1 ja c = Bc ,  B[ab] = Bab,  B = у  Jb,a  Babc =    2  Jb,c,

B ab          ¹ та     vc         ¹ та     TOah   oc ababc   a be be]    a> _ 6

c =у J'bw,  Bab = ’У Jb,c,  Be = Bab,  B = B ,  Babc = Ba[bc], and a : X(M) x X(M) ^ X(M) is the second fundamental form of the immersion of the hypersurface M2n—1 into the manifold N2n which is symmetric (aij = aji, i,j = 1, 2,... , 2n - 1) such that VxY = Vx Y + a(X, Y) with V and V are the Riemannian connections of N and M respectively (see [19]). Further, a,b,c = 1, 2,... , n - 1, while a,b,c = 1, 2,..., n and w = wn = wn.

Definition 6 [20]. A submanifold (M2n-1, g) of Riemannian manifold (N2n, h) is said to be totally umbilical if aij — Xgij, where a is the second fundamental form, X is constant and i,j = 1, 2,... , 2n - 1.

Definition 7 [21]. A submanifold (M ^{2 n - 1} , g) of Riemannian manifold (N ^{2 n} , h) is said to be totally geodesic if the second fundamental form a vanish (i. e., a = 0 ).

Definition 8 [7]. A submanifold (M ^{2 n - 1} ,g) of Riemannian manifold (N ^{2 n} ,h) is said to be minimal if it satisfies g^{p s} a _ps = 0 , for all p,s = 1,..., 2n - 1 , where g^{p s} and a ps are the components of g ^{- 1} and the second fundamental form a respectively.

3.    GK-Manifolds as Hypersurfaces of V G-Manifolds

Theorem 4. The hypersurface of a Vaisman-Gray manifold (N ²ⁿ ,J,h) admits a generalized Kenmotsu structure if and only if its second fundamental form σ has the following components:

^a ab ^- — ¹ 1 2 F ab ⁺ — 2 B nab ⁺ ^ 2 B an },

° rib = ^ nn

= 0,

-

-

? 2 ^a n

_{δ a}b _,

σ ab

-

3 F

’ab | ^— 2 B nab

+ -1= B abn} ,

σ

a b

σ b a

-

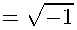
-2 a”}

where aa = aa = 0, an + an -272,  Fab = V2Bnab = -2- Babn,  Bnbn = Bnbn = 0,

F~ 7 = —2 B - 7 = ab         nab

-

— R -

5 B abn ’

_C abc

=B

abc

. abc abc

⊳ Suppose that N is V G -manifold, then Theorem 2 gives:

B [ abc ] = B     B abc = B abc ,  в = B abc ,  B ab = „^ 4 ,   B ab = „^

where a,b,c — 1, 2,..., n . Therefore, comparing Theorem 3 with Theorem 1, we have

• 1)    B a^b - 0 , B ^abc

7 2 B an

|

2 F ^ab } ;

_ abc aa

= C , ^a b

Т-Г{V2 B an + 5 a} , ° ^ab - -V-1 {72 B ^nab + 7 B~ n^b +

• 2)    B ^c ab

= ⁰ , B ale

a

= C abc , ° a

-—- 1 {V² B abn + ⁵ a } , ^a ab = —— ¹ { B nab ⁺ 772 B ab ⁺

^/2 B abn ⁺ 2 F ab } ;

• 3)    ^ B nab - F ab ,  2 B nab - F ab . a a - -TP {B na - B ab} , a nb - V^- {B nSn + B n} ,

° n - — V— 1 {B ^nbn + B n^b} .

Since B a^b - B^c- - 0 , then a a - a_a - 0 . So, we have B a^b - B n - B n^b - B n - 0 . ^c       ab                       ^{a                        n}       ab ⁿ       nb

Now, since a is symmetric then °[nb] - 0. Regards item 3) above we get B[nb]n - Bnbn -0 - B[nb]n - Bnbn and this implies that anb - an - 0. As well as, a[ab] - a[ab] - 0 and this implies that —2Bn[ab] +   B[ab]n + 3F[ab] - 0. Then, we get:

72 B ^nab

^R

+ ^B' 72

:abn + ³ f ab

¹ R abn I ⁵ Tbab

— 2    ⁺ 2

- 0 .

• So,    we obtain the results. Also, equating the values of a a in items 1), 3) and uses the above results, we have

  _-

  
  

  7-1

  
  
  
  
  
  
  

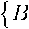
  na b

  
  

  - Bn.} - ^{^Br + 5a}•

  
  

  B na + B n, - ^ ■

  
  

Since Bna - OnSa - 1 an5a and Ba- - 1 an8~, then an + ari - 2—2. So, from the above b            b 2 b          nb 2 n b                   n discussion we attain the requirement. ⊲

Corollary 1. The hypersurface of VG-manifold does not has conditions more that the con ditions of above theorem as well as Babc - Baba - 0, if it has SGK 1-structure.

⊳ The proof is the same of proof Theorem 4 and the addition condition is attain from Definition 5. ⊲

Theorem 5. The generalized Kenmotsu hypersurface ( M ^{2 n - 1} , Ф,^,П, g) of a Vaisman-Gray manifold is totally umbilical if and only if, it has

^B nab = B nab ,   B ab = B nab ,   a^ — A = У- г{1 --L a"}.

⊳ Suppose that M is totally umbilical GK -hypersurface of V G -manifold, then according to Definition 6, we have a ij = Ag ij . So, if we use the values of a in Theorem 4 and elements of g in Remark 1, that given by:

/ O	O	I n - 1
( g ij ) — 1      0	g nn — 1	0
\ I n - 1	O	O

i,j = 1, 2,..., 2 n - 1,

and substitute them in the last equation, we obtain ann — Agnn — A, ab — Ag*b —

λδ ^a b

-

- 4

^a *b = ^A g ab = ⁰

2 ^F ab + — 2 ^B nab

^^

+—/= B,

— 2   abn

³ F. + + - 2 B

₂ ab        "ab

-

⁵ F -

2 F ^ab

- —2 B -7. ab         nab

Since F [ ab ] — F ab and B _n[ab] — B _nab , then we have the result. The converse also hold true. О

Corollary 2. The GK -hypersurface of V G-manifold is totally geodesic if and only if, it is totally umbilical with a " — a _n — \/2-

⊳ The proof is directly form Theorem 5, Definition 7 and Definition 6. ⊲

Theorem 6. The generalized Kenmotsu hypersurface of a Vaisman–Gray manifold is minimal if and only if, it has a(£, £) — 0 .

⊳ According to Definition 8, we getting on the following:

0 <>

ps        ab g aps — g aab

+ S aba. - ab

— *

+ g ab a®

+ g ab a

ab

+ gⁿⁿv_rm —

— * g^a4 b

-T g aab + ga aab + ann — 0— *

Then from Theorem 4, the foregoing equation reduce to g ab a -b - g ab a a* + a _nn — 0 ^^ a _nn — 0 .

So, we have a(£,£) — 0 . О

Theorem 7. The hypersurface of a Vaisman-Gray manifold has SGK ^ -structure if and only if, σ has the following components:

+ g ab a

ab

+ ^a nn

a ab ^—

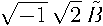
b nab,  anb — an

— 0,

σ

b a

-

i „ Lb — T 2 ^anf ° a ,

a ab _—

.       2 B nab ,

a σ _b ^a

-

—2 ^a‘} <’

where aa — aa — 0,

α ⁿ

+ a n — 2^2,

_B nab

_ B abn    B

nab ^{— B} abn ^{— 0 , B}

abc

— C

abc

,    ^B abc ^— C abc ,

^^

nbn

— B^nbn — 0.

• <1 Definition 5 and Theorem 1 given Cartan’s structure equations (first group) of SGK 2 - manifold as follows:

d^a = wa Л wb + Cabc Wb Л Wc - 5b wb Л w, dwa = -wb Л wb + Cabc wb Л wc — 5b wb Л w,                    (3)

dw = 0.

Now, comparing equation 3 with Theorem 3 and take into account the technique of the proof of Theorem 4, we have the results. ⊲

Theorem 8. The hypersurface of a Vaisman–Gray manifold admits Kenmotsu structure if and only if, a has the same components in Theorem 7 under the same condition with

B

abc

= B-r- abc

= 0 .

⊳ The claim of this theorem is attains from Theorem 7 by using the definition of Kenmotsu manifold that mentioned in Definition 5. ⊲