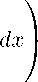On Some Interpolation Inequalities Due to Olga Ladyzhenskaya and Nonlinear Partial Differential Equations

The subject of interpolation inequalities is so vast that it is impossible to describe even short history of this question, so we confine ourselves to refereing to books [1, Ch. 5, Ch. 6; 2, Ch. 1; 3, from section 1.6 and throughout], and the references therein.

From the previous papers with aggregate results on the interpolation of norms between different scales of function spaces we mention only the papers [4–10], where the more comprehensive bibliography can be found. Here the papers [4] and [5] deal with interpolation inequalities in the Lebesgue and the Sobolev spaces involving the H¨older norms (similar to the present paper). Moreover, the papers [6, 7] contain multiplicative estimates of the Lebesgue and the Sobolev norms over the Lebesgue and the Besov norms, including the limiting the Holder case B 2 , ^ = C ⁷ . On the other hand, in the papers [8, 9] multiplicative interpolation inequalities between the H¨older (or BMO) and the Lorentz norms of a function are proved. Besides, inequalities from [9] bind together the Lebesgue or the Sobolev, the Lorentz and the Besov–Lorentz norms. Mention also that the inequalities from the paper [10] include BMO norm.

Thus the present paper can be viewed as an extension of the results in [4–10] to the anisotropic “parabolic” case and with another proof. Moreover, the present paper is motivated, in particular, by [11], where the simplest situation was considered, and where we got the idea of simple proof for such sharp inequalities. Note also that in this paper we consider for simplicity the known functional spaces, designed for parabolic and elliptic equations of the second order.

Let us now give several definitions and auxiliary facts. We are going to use standard spaces C ^m+a (Q) and C m ^{+ a}, m^ (Q T ) of the Holder continuous functions u(x) and u(x,t), where m = 0,1, 2,... , a G (0,1), Q is a given domain in R^N (bounded or unbounded) with smooth boundary (of the class C ^m + ^a ), Q T = Q x (0,T), Q T = Q x [0,T], T >  0 is a given constant. The norm in the space C ^m+a (Q) is defined by

Mc.~<® = l< ^+a) = l< ’ +       '■               (1)

where

MOm ^- E max I D ^{e u ( x )} l ^, < u > ?m ^{+a) -} E < D ^e uM^) ^{,          (2)}

| в |< т                                        | в | =т

/W^W  /^El = SUD ^{| w ( x )} - w^{( y )l}

\w(x)/q - \w(x)4,Q - xsup   |x - y|a , в = (в1,в2,... ,eN) is a multiindex, ei =0,1, 2,... , |в| = в1 + в2 + ... + eN,

D e      д ^{в 1} d ^e ... d ^e N u(x)

x u   ^вТ^^1вт^^{2   в}^^к '

x ₁ x ₂ . . . x _N

Analogously, the norm in the space C ^{m + a}, + (Q t ) is defined by (k, l are positive integers)

Mc m-m j a (Q t ) -      ' = HOT +                     (3)

^|„^|L ^m)=    E тпя^¹ rine^r t\\   i^\ ⁽ m ^{+ a )    /}_1l\ ⁽ m+^{a )} ^/_1l\ ⁽ m+^{a )}

^{| u |} q _t ^— max \^D t ^{D x} u ^{( x,t ) 1 ,}   \u/ q _t       \u/ _x, q _t  + w t, Q T ,        (⁴⁾

| в | +21 < т T

WE - E  №в"-П "-, x,Qt                     \ x x, q^V

0 < m -| e |- 2l < 1

, . \                                              ( m ^-\ ^e \^- 2 i +^a \

' - E    / D t D u(x».J       ’                (5)

0 ^ m -| e |- 2l ^ 1

Note that for the space C ^{m + a,} 2 (^ _T ) we also have the estimate (see, for example, [12])

* m -^-2 l + a \

< u > tm+ ^a) =    E   DDux^ ²

0 < m -| e |- 2l < 1

< C (Xa) + D'-    2   ’) • x,T                          t, where here and everywhere below we denote by C and ν all absolute constants or constants depending on fixed data of the problem. It is known (see [3, 5, 13]) that the seminorm (и)^+аа

LT is equivalent to the seminorm

< u >£ ^+a) - ^c» (.

sup

,h E R 3 ; x, x + h E L; t E [0 , T ]

^{| A} k,h u(x,t) l

| h | ^m+a

+ sup

At>0; x E L; t E [0,T]

^{| A} t,At ^{u ( x,t ) |} | At | m^

Here k and l are some fixed integers such that k>m + a, l > m + a, AkT- u = Axh(Ak-1u), Axh u = u(x + h,t) - u(x,t) x,                , x,h                 , and analogously

A^ A t U = A t,At (A t,2 _t u),  A t,At “ = u(x,t + At) - u(x,t).

The above relations can be written also in a more concise way. Denote H = (h, At) ,

||H|| = |h | + |At|2, and denote Ahu(x, t) = u(x + h,t + At) — u(x, t). Then (7) is equivalent to

< > (m+a)    „                    | ^A„ ^{u ( x,t ) |}

.

u> L t  ^- C     ^SU P_  IH^m+T-

( x,t), ( x,t )+ H eL t \\H ¹

We also use for functions u(x) or u(x,t) spaces L _p (Q) or L _p (& t ) respectively with the norms ||u||p Q and IHlp ^ T correspondingly, p> 1.

For the spaces C ^{m + a} (^) = C ^l (^) with noninteger l = m + a and also with integer l ^ 0 we have the following interpolation inequalities (see, for example, [2])

|< < C’)K)1

_ l — 1 1 = l 2 — 1 1 ,

l 1 < l < l 2 ,                 (9)

and analogous inequalities for anisotropic spaces C ^l, 2 (Q t )

К < C(Iu g)“(I u ^r ■

= l — 1 1

^l 2 ^{— l} 1 ,

l 1 2 ,             (10)

where l 1 , l 2 may be either integer or noninteger.

The further content of the paper is as follows. In the next section of the paper we prove some interpolation inequalities for functions from the H¨older spaces (in the case of unbounded domain we need the intersection of the H¨older and the Lesbesgue spaces). And in the last third section we apply these inequalities to a priori estimates and solvability of a model (just for simplicity) problem for partial differential equations.

• 2.    Interpolation Inequalities

We start with the following interpolation inequality as the key particular case.

Lemma 1. Let l >  0 be a positive noninteger and let u(x,t) G C ^l, 2 (Q t ) П L _p (Q t ) • Then

КcC 00“

If for the function u(x, t) the following parabolic norm is finite sup llu(->t)llp,n < re,

0

1&

0

<1 We are going to use relation (8). Let first Q = R^N, T = 00. Let x,y G R^N, x is fixed, t,т > 0, t is fixed, h = y — x, At = t — т, H = (h, At), k is an integer, k > l, e > 0. Represent u(x, t) in the form

Aw u     kA

u(x,t) = AHu + C^Ciu(x + ih,t + iAt) =     l, ||H|| + У^Ciu(x + ih,t + iAt),(14)

i=1                             ||H 1

where Ci, i = 1,..., k, are some integers, depending only on k. From this we obtain

k

|u(x,t)| C C(u^nxR1 ^H|l + ^Ci\u(x + ih,t + iAt) I i=1

with some constants Ci, R^ = {t ^ 0}.

Raising this inequality to the power p > 1 and applying the inequality

(Й a)

N

< NT aP, i=1

N G N, ai > 0, i = 1,...,N, p> 0,

we obtain

k

|u(x,t)|^pC C [{_и(^_хxR )p ЦПl^pl + C£^Г(х + ih,t + iAt).          (16)

i=1

Integrating in (y, т) over the cylinder Q_s(x, t) = {(y, т) : |y — x| C e, t C т C t + e²}, we get

Ce^N+2|u(x,t)|^pC C <       _xR+)pe^N+2+pl + C^ J |u|^p(z,0) dzd0,     (17)

i = ¹Qi_£(x,t)

where for each i in the sum we made the change of the variables z = x + i(y — x), 0 = t + i(т — t) and we took into account that for each i we have (y — x) = (z — x)/i. If the norm in (12) is finite, we can integrate just in y over the ball B_£(x,t) = {y : |y — x| C e} and obtain

Ce^N\u(x,t)l^P C C ({ARN_xR+ )pe^N+pl + Ci£    J |u|^p(z,t + iAt) dz.    (18)

i^¹Bi_E(x,t+iM)

Estimate now the integrals over Qi_e(x,t) in (17) by the integral over R^N x R^, divide both sides of (17) by Ce^N+2 and take the roots of power p from the terms of this relation. As a result we obtain

^|u(^x,^t)| ^ C^u^RN_XR+ + C^e + ll“llp,RN_XR+ , or, taking supremum over (x,t) G R^Nx R^,

Optimizing this inequality with respect to e > 0, or just taking e =

/ ll“llp,RNXR+ \ pl+N+2 \ ^RN xR+ / with HRN xR+ = 0, we finally obtain

N+2                        i

I“|RNxr₊ « C («RNxR.)^pl+N+2(H“IUn xR. ) p^

that is exactly inequality (11). If now (u)RN_xri = 0, then from (19) after letting e ^ w it follows that |u|RN_xr! = 0 and so (20) is valid in this case also.

If the norm in (12) is finite, completely analogously to (20), we have subsequently from (18)

|u(x,t)| < Cel^u^RN_xR1+ Ce-N sup ||u(>t)||p,RN,

⁺           teR1₊

^{1 u|}rN_xR+ ^ C^^RN _xR₊^{+ Ce}p sup ^Iu⁽^^,t)IP,RN , and, optimizing this inequality with respect to e > 0,

^|u|R^NxR+

< C

N

(l)     1 ^ pl+N I

+

sup teR^.+

pl pl+N

that is exactly inequality (13).

Now in the case of general smooth domain Q = RN and T < w the lemma follows by an extension of a given function to R^Nx R^ with the preserving of the corresponding norms up to a multiple constant (the way of such extension for smooth domains is described in, for example, [14, Ch. IV]). The lemma is proved. >

Now we can easily get the following more general assertion.

Theorem 1. Let l be any positive number and let I2 > l be a positive noninteger. Let also u(x,t) G Cl2,~ (Qt) A Lp(Qt). Then l< < C (1“^)“     ^)1-“, - =           •            (21)

If the parabolic norm sup ||u(-,t)||p,Q < TO

0

• I.    « C (lull1)' Qx HuM)IU)   • ’ = p N(22)

• <1 From (10) with li =0 we have

l1

At the same time, from (11) it follows that

(0)          \(2 Ш          \1-w

Hqt ^ C (\^u\r_T) (llullp^T)    , ^- = i₂p₊N + 2 •

Substituting this estimate for H^) in the previous inequality, we obtain ⁱT

12 —1

К < C (K)¹²[(К)   ' «и«пт) p^] ~

,     . _x pl+N+2                 p(1₂—1)

= C (|u0 ²    (IMt) 1

that is (21). Inequality (22) is completely analogous on the base of (13). The Theorem is proved. >

By exactly the same arguments we have also an assertion for isotropic the H¨older spaces in an “elliptic” case.

Theorem 2. Let l be any positive number and let I2 > l be a positive noninteger. Let also u(x) G Cl²(Q) П L_p(Q). Then

I< < C (K2T «ulp/-' - = ^         (23)

In the next section we give some simple application to an initial boundary value problem for a quasilinear parabolic equation, mostly to illustrate the idea of applications.

• 3.    Solvability of a Quasilinear Initial Boundary Value Problem

Consider the following initial boundary value problem in a bounded domain Qt unknown function u(x, t)

for an

∂u

— -Au + |u|^{q 2}u = f (x,t), (x,t) G Qt ,

u(x, t) = 0, x G dQ, u(x, 0) = uo(x), x G Q.

Here f (x,t) is a given function, uo(x) is a given initial datum and we suppose that f (x,t) G Ca2 (Qt), uo(x) G C2+a(Q),  2 ^ q< 2 + N.

We note again that we consider the case of a bounded domain Q just for simplicity of estimates. (In the case of an unbounded domain we can consider the data of the problem to be from an appropriate the Lebesgue spaces, besides (27).) We are going to prove carefully only a priori estimate for a solution to problem (24)-(26) in the space C^2+a,2 (Qt). The existence and uniqueness of the solution can be proved after this in a more-less standard (nowadays) way (see, for example, [2, Ch. 7]), about the quasilinear parabolic equations. Namely, we have the following assertion.

Theorem 3. Let a E (0,1). Let, further, a function u(x,t) E C2+а, + (Qt) satisfy problem (24)–(26). Let also qa + (q — 1)(N + 2) в _ q [(q — 2)(2 + a) + 2] q(2 + a) + N + 2 ,    =  q(2 + a) + N + 2

There exists a constant C > 0, which does not depend on f (x,t) and uo(x), with

B q(i-A)

T

У У f ²x t) dxdt⁺у u^2(x)dx 0 Q                   Q           .

<1 First we get some integral estimates for u(x,t). Multiply equation (24) by u(x,t) and integrate over Qt. After integrating by parts in the first two terms of the equation with taking into account the boundary and the initial conditions we get

TT

¹/ ,„,„... у>.,²„-^d„ =

T j'ff              ■.2 У u0(x)dx.

0 Q

Q

For the first term in the right hand side of (30) we have

T

У У f (x, t)u(x, t) dxdt 0Q

« IlfI|2,QtM2,Qt< iT + | ||f ||2,Qt

T

=' Il"'

TT  T dxdt +—У ff 2(x,t) dxdt < 'Cl J У । Vu ।2 (X’t) dxdt +—У У f 2(x,t) dxdt,

where we took advantage first of the H¨older inequality, then of the Cauchy inequality with ε, and then of the Poincare inequality. Taking into account this estimate, choosing ε such that 'Cq = 1/2, and absorbing the term with ' into the left hand side of (30), we obtain

T

T

Уu²(x, T) dx + У У | Vu 1²dxdt + У У | u |^qdxdt< C

Q               0 Q              0 Q

T

У У f²(x, t) dxdt + У u2(x) dx

0Q

Q

. (31)

Thus, in particular, we get the following estimate llullq , Qt

< C

T

11f ^t)

dxdt +

u²₀(x)

Q

q

Now we are ready to obtain a priori estimate for a solution to (24)–(26) from the space C²+^a,~(Qt). Let us apply inequality (21) to estimate the norm of the term |u|^q-2u in the space C^a, a (Qt). Note first that by elementary considerations we have

II-a « C ОСГОЮ

Use (21) with I2 = 2 + a, li =0, p = q to obtain

• 1    ug) < C (\u\2+a) I"0 (||u|l й)1-Ш0, wo = ----N+2------.

I Ia; V Iqt ;       "qAA ’    0   q(2 + a) + N + 2

Then use (21) with I2 = 2 + a, li = a, p = q to obtain also

I I (a) / Л fI |(2+a)\"a /'ll        \1—"a               qa + N + 2/or\

Mar < C          (||u|U)   ■ “a = qp + aTN+^.

From (33)–(35) it follows that

II«HulC < C (|u\a+a))A (WU,)B.

A = (q - 2)“о + “a. B = (q - 2)(1 - 4,) + 1 - “a are defined in (28). On the base of the condition on q in (27) we have A < 1. So, applying to (36) the Young inequality with ε, we obtain

Ii uiq-2 u|£ < фС'+C1-1 '-1-3 (и.®-) '-A ■

Moving now the term |u|q-2u to the right hand side of equation (24) we represent it in the form dt - Au = g(x) = f (x, t) - |u|q-2u,   (x, t) G Qt.

Now we use the well known estimate in H¨older spaces for a solution to initial-boundary problem (39), (25), (26) (with the given function |u|^q-2u) to obtain

I u|T’ « C 0^ + ^>O) < C (If |£ + |uo\(T^a)+ lluIqAg)

«C (If I®) +     ⁺) + C^igr’+C^1-3(И.&)^1-3

B

« Сф^О + C ОС + Ы0А) + C' 1-3 (//f’fX'fdxd1 + /UOdx)

\ о aa / where we took advantage of (38), and then (32). Absorbing now the first term with sufficiently small e (Ce = 1/2) into the left hand side of the last inequality, we arrive at the estimate

B

«('--)

T

У Уf2(x. t) dxdt + У u0(x) dx о aa .

that is at (29). Theorem is proved. >

Note that, of cause, the estimate of the kind (29) can be obtained in some other ways. For example, starting with estimate (31), one can consider problem (24)–(26) in the Sobolev spaces first (under even weaker restrictions on the exponent q). And then one can use some bootstrap arguments to gradually raise up the smoothness of the solution with some corresponding estimates. For example, we can first consider the problem in the space W2q1 (QT) when the q-1

term |u|^q-2u∈L q . Well known results on parabolic equations in the Sobolev spaces give q-1

us the solution from W2^ (Qt). Then the Sobolev embedding gives us that u G Lp1 (Qt) and q-1

depending on q and n it may occur p1 > q. Now we can repeat the considerations in the space W2p^_(Qt) to obtain u G Lp2(Qt) with p2 > p_. And so on till by embedding u G C^£(Qt)

q-1

with some e > 0.

Our goal was just to demonstrate how easy it is to apply the interpolation inequalities from section 2 to a priori estimates of solutions to nonlinear PDE in smooth classes of functions.

Acknowledgement. The author is sincerely grateful to the Editorial Board and to the unknown Referee for working with this paper and for more than just valuable comments.