On the scheduling problem of cargo transportation on a railway network segment and algorithms for its solution

The formation of a cargo transportation plan consists of two parts: formation of a timetable for train (car) traffic along the railway network, assigning locomotives to trains for carrying out transportation. These problems are solved separately due to not only computational difficulties but even difficulties in constructing mathematical model that allows to solve these two problems together.

We single out [1–5] among publications devoted to the problem of assigning locomotives to trains. The papers [1, 2] solve the problem of assigning train locomotives to trains with goal to minimize the number of locomotives in usage and fulfill the transportation plan. The works [3, 4] consider the problem of assigning train locomotives with a criterion of cost minimization. The paper [5] solves the problem to optimize a shunting locomotives traffic along a railway station. In [5], the goal of optimization consists in performing all shunting operations and reducing time in the shunting locomotives traffic.

We note [6–11, 13] among the publications devoted to the problem of scheduling train traffic. The work [6] provides a detailed overview of the early 21st century publications on this problem. The paper [7] considers the scheduling problem for trains going in one direction along a single-track track with the possibility of overtaking at stations. This problem is reduced to an integer linear programming problem. The work [8] considers the problem to create a cyclical timetable taking into account delays in the execution of the timetable. The paper [9] considers the problem of forming trains, schedules and routes to destination stations. The optimization criterion is the minimization of the total weighted time of order fulfillment. Integer formulations of this problem are proposed taking into account the limitations that arise in practice. The work [10] considers the problem of constructing two-way train timetable between two stations connected by a single-track railway with a siding. The dynamic programming method is used to solve this problem.

The work [11] presents a polynomial algorithm for adjusting train timetable for the case when some track of a double-track railway becomes unavailable, the remaining track contains a siding. All trains are divided into two categories: priority and regular. Such problems can arise, for example, when a track is closed for a repair – during track possession [12]. The closest work to the material of this article is [13]. In this work the problem of scheduling train traffic along the railway network is considered. Traffic along the railway network is carried out only at certain intervals of time – using “subthreads”. The present work continues and modifies [13] in reducing number of variables in the optimization problem and constructing new universal optimality criterion for the forming of train timetable along the railway network.

In this paper we investigate the problem of constructing optimal train timetable using a railway network segment multigraph. The traffic along the railway network multigraph segment is carried out at certain intervals – using “subthreads”. The formation problem of optimal timetable is reduced to a mixed integer linear programming problem. An algorithm to find a suboptimal solution is proposed. A meaningful example is given.

1.    Basic Notations and Assumptions

Let us consider a railway network segment represented by an undirected multigraph G =< V,E >, where V is a set of vertices (stations where the railway network branches, stations whose number of incoming tracks is not equal to the number of outgoing tracks, marshalling yards, terminal stations) and E is a set of edges (railway tracks) connecting these vertices. Let |V| = m. By renumbering vertices of multigraph G from 1 to M we compose the set of indices V ‘ = {1, 2,..., M }. Each element of this set uniquely determines the vertex of the multigraph G. Impose restriction that M > 2. Otherwise, railway segment consists of only one station and it is meaningless to make transportation plan.

Suppose that we have I trains, for each of which the following is given:

• •    index of departure vertex v_i^dep.∈ V ^′;

• •    index of arrival (destination) vertex v_i^arr.∈ V ^′;

• •    time of readiness for departure t_i^dep., which is calculated as the number of minutes from some initial instant of time;

• •    maximal amount of time di during which the train is allowed to be at the departure vertex from the moment of readiness;

• •    train travel time T_i, i.e. maximal amount of time during which the train is allowed to be on the railway network (excluding time at the departure vertex) computed in minutes.

2.    Construction of Mathematical Model of Train Traffic Along Railway Network Segment Multigraph

Train traffic along railway hauls (between vertices) can only be carried out at certain intervals. To describe such intervals, following [14], we use a set of conflict-free “subthreads” Z . Each element zk of this set represents 5-element row zk = (vbeg., Vend, nk, tbeg., tend), where vbeg. G V‘ is the index of starting vertex of movement, vend £ V‘ is the index of ending vertex of movement, moreover vbeg. and vend are indices of adjacent vertices in the multigraph G, nk is the number of the track connecting vertices with indices vkbeg. and vkend , tkbeg. is the starting time of movement, teknd is the ending time of movement. We suppose that dimZ = K and renumber elements of the set Z from 1 to K . Thus, a number from 1 to K determines parameters of the “subthread” uniquely.

Train traffic may be restricted due to the train stop at intermediate stations (between departure and arrival stations) along the route. For example, there must be a change of locomotives, the uncoupling/coupling of cars at some stations and some stations on the opposite must be passed without the train stop. Therefore, we introduce minimal and maximal possible duration of stay at the station with the vertex index v _k ^end after using the k-th “subthread” by the i-th train: t St.min and t St.max. , i = 1, I, k = 1, K.

i,k               i,k

We denote duration of the forecast period by T _max. . If the timetable is scheduled on a day (1440 minutes), then T _max. = 1440.

Let us formulate the mathematical model of train traffic of the noted above I trains along the railway network segment given by the multigraph G on the base of the “subthreads” set Z . We refer to a range of “subthreads” used by a train for movement as a route. As a consequence it is possible to determine a range of vertices sequentially crossed by this train from the route. We limit the maximal amount of “subthreads” in the route by some predetermined number J. By the j-th phase of the route of the i-th train we mean a movement of this train when the j -th “subthread” is used in the route, i = 1,I, j = 1,J +1.

Let us introduce auxiliary variables δ _i,j_,k characterizing the usage of the k-th “subthread” by the i-th train at the j -th phase, i = 1,I, j = 1,J + 1, k = 1,K .A variable 5 i,jk is equal to 0 if the k-th “subthread” is not used by the i-th train at the j -th phase, and 5 i,j,k is equal to to 1 otherwise.

Using the introduced variables we form a set of feasible strategies. By definition of the variables δ i,j,k , we have

5.jk £{0, 1}, i = 1J,j = 1,J +1 ,k = 17K.(1)

To depart trains from its departure vertices, we introduce the constraints

K

52 5i,i,k = 1, i = M, k=i

K

E 6.1k«4* = vdep, i = 17-(3)

k=i

To depart trains not later than d i from the time of readiness for departure, we impose the constraints

K

E ^SWt^^ t + d . , i I                   (4)

k=i

To ensure that the start of movement is not earlier than the time of readiness for departure, we use

K trp< E^kt    = 1I.                    (5)

k=1

We cut off the possible use of routes with cycles, i.e. we use only simple paths along the multigraph G for each train

J +1

E E    ⁸ 3 <  !• i = 17, m = ГМ.            (6)

3 = 1 tafr^m , 1

k

Traffic along the multigraph G can only be along the adjacent vertices

K

δi,j,kvkend k=1

K

< E* - j +i ^beg *

k =1

( 1 - E ⁸ ij + ¹ ’kJ ^{M 3 ,}

KK

E ⁸ - 3k    >  E j +1

k =1               k =1

¹ - E ⁵ 3+1 ’ k^

M, i = 1,I,j = 1, J - 1.

It is necessary that “subthreads” are docked in time, i.e. the arrival time at some vertex of the multigraph G must not be more than the subsequent departure time from the same vertex. And taking into account the duration of stops at intermediate stations on the route, we get

KK

K

1 - £5- , j+1,k Tmax., k=1

E 5 ij,k (t k^nd + t$ k min. ) < E 5 ij+1 k t^ g' + 2

k=1

KK

E5i,j,k(tknd + tstkmax') > E5-3+1,ktbg', i = ^Tl,j = M-T.(10)

k=1k=1

Arrival at the destination vertex is possible in no more than J phases. That is why we introduce the constraints

IK

EE 5-J+1,k = 0,(ii)

i=1 k=1

K

δi,j,kvkend k=1

KK

^{1 -} E ⁵ i’3’k ⁺ E ⁵ i’3 + 1,k )

M +

k=1k=1

+

KK

E 5 -jk - E 5 -3+1^ v ?"'

k=1        k=1

i = l.I.j = 1, J,

K

δi,j,kvkend k=1

KK

E 5 -3^ - E 5 ■ ■ i v ?⁴

k=1        k=1

i = ^{1 ,I,} j = ^{1 ,} J.

Let us comment constraints (7) – (13). Due to the presence of constraints (1), components of the vector

KK

δ i,1,k ,       δ i,2,k ,..

k=1      k=1

K

. ,        δi,J,k , k=1

K

δ i,J+1,k k=1

can only be nonnegative integers. In connection with (2), the first component of the vector 5 i is equal to 1. If the second component of the vector 5 i is equal to zero, then constraints (7) – (10) are fulfilled. Constraints (12), (13) hold then the train arrives to the destination vertex. If the second component of the vector 5 i is equal to 1, then constraints (12), (13) are fulfilled, constraints (7) – (10) hold, since the condition of docking “subthreads” in place and time must be met. Namely, departure and arrival must be from the same vertex, departure time must not be earlier than arrival time from the same vertex (taking into account train stop at the station). If the second component of the vector δ _i is equal to K

k* = 22 5i,2,_k > 2, then constraint (7) is not fulfilled. It is connected with the fact that k=1

maximal value of the right side of constraint (7) is negative, since by assumption M > 2 and

K

E 5»k vbeg. + k=1

KK  K

M ³ =

1 -      , 2, k  M3 <      , 2, k M + 1 -E 5i, 2, k k=1               k=1                  k=1

= k * M + (1 - k * )M ³ < max k * M + (1 - k * )M ³ = 2M - M ³ < 0, k ^∗ ≥2

while the left side of this constraint is positive since vertex indices are positive. Likewise, anywhere in the vector 5 i after 1, there are only 1 or 0. Note that, in the vector 5 i , after 0 can be only 0 because constraint (8) is violated otherwise. If there is 1 after 0 in the vector 5 i , then the left side of (8) is equal to 0 but the right side is equal to some positive number. If there is some number k > 2 after 0 in the vector 5 i , then

K

δi,j+1,kvkbeg. - k=1

KK  K

1 - E  +i,k m > E §ij+i,k - 1 - E  +i,k m = k=1                k=1                 k=1

= k - (1 - k)M > min k - (1 - k)M = 2 + 2M - 1 > 0.

k˜≥2

At the same time, the left side of (8) is equal to 0. Thus, the vector 5 i is a range of ones followed by a range of zeros. The vector δ _i is guaranteed to have at least one zero due to constraint (11). And this leads to the fact that the given system of constraints sets the route from the departure vertex to the arrival vertex while at each phase exactly one “subthread” is reserved.

Any “subthread” can not be used by more than one train

I J+1

EE ⁶ W <  !• k = 1K i=1 j=1

Note that it is possible to determine rigidly specific edges of the multigraph G which are sequentially intersected by the train within the framework of the constructed model.

To this end, at each phase, we need to impose the following constraints:

E ^ i,j,k = 1, i = ¹, ¹ , j = 1, J i , k.k e K j

K

E ^ijk = °, i = 1,I,j = Ji + 1, J +1, k=1

where K i C {1,..., K} is a set formed by numbers of “subthreads” that admissible for use by the i-th train at the j-th phase according to a predetermined sequence of edges of the multigraph G for traffic, and J _i ^∗ is the number of phases required to arrive from the departure vertex to the destination vertex.

To ensure that train travel time is limited by T _i , we impose the constraints

E j t™^d - E ⁶ i1k t bg - T, i = 1-I’j = 1-J'            (15)

k =1             k =1

3.    Choice of Criterion to Form Optimal Timetable of CargoTransportation

To form a transportation plan, we use the criterion which consists in the minimizing of total time spent by trains on the railway network segment from the moment when trains are ready for departure. Before scheduling, it is not known how many phases a particular train needs to use for arriving to the destination in the constructed model. Therefore, the criterion should be formed from three parts: the total time of trains at railway hauls, the total parking time of trains at intermediate stations in their routes, the total parking time at departure stations from the time of readiness for departure. To obtain the total parking time of trains at intermediate stations, we introduce auxiliary variables T i,j and additional constraints

KK

T i j > ^j k t^g - Y/wt^ , i = 17,j = 1J.         (16)

k =1                k =1

Optimal value of the variable T i j characterizes the time spent at the (j + 1)-th station in the route (except for the destination station), j = 1, J. Taking into account introduced variables and constraints we obtain the following optimization problem

+

I J +1 K

EEE ⁶ - jk (t i =1 j =1 k =1 '

end k

_{- t k} beg ₎

v

the total time of trains at railway hauls

IK

I

EE ⁵« k t?g - Et?p

→

+

IJ

EE T i, j i=1 j=1

the total parking time of trains at intermediate stations

~

min

Л

+

.

i =1 k =1 ^.

i =1

t 1 , t 2 , 6 i,j,k , T ij >0, i=1, I, j = 1, J +1, j=1, J, k=1 K

sz

v

the total parking time at departure stations from the time of readiness for departure

Note that the second term in (17) is responsible precisely for the total parking time of trains at intermediate stations. Since if there is a need in only one phase for movement for the i-th train, i.e.

kk

£ ⁵W = 1 ТА^ ^{= 0} - j = 27JTT, k=1            k=1

then, according to (16), the value Тц is not less than some negative number. But, according to the constraint T ii > 0, it is true that Т ,,1 > 0 and other constraints (16) for the i-th train are transformed in the constraints T ijj > 0. Since there is the minimization problem, then, on an optimal solution (if this one exists), it is true that T ii = T i,2 = ... = T i.j = 0. Sum of these variables is equal to 0 that should be in the case of only one phase for movement as in this case there are no intermediate stations between departure and destination stations. If the i-th train uses j * G [2, J ] phases for movement, i.e.

k

^ 5 i,j,k = 1, j = Ij, k=1

k

^ 5i,j,k = 0, j = j* + 1,J + 1, k=1

then, due to constraints (16) and "T^ j > 0, we have

KK

T ij > £ 5 _г,₃ +i,k t beg - £ j cd- , j = ij-r, k =1                k =1

Zs                                          ________________

T ij > 0, j = j * , J.

Since there is the minimization problem, then the last constraints are active. This leads to the fact that the second term in (17) characterizes the total parking time of trains at intermediate stations (for the i-th train there are j * — 1 intermediate stations).

One or another part of criterion (17) may be more prioritized for a person who makes the transportation plan. Therefore, we modify criterion (17) and solve the problem

I J+1 KI J ci SEE j t — t) + C2 EE T ■ i=1 j=1 k=1                           i=1 ˆj=1

IKI

\i=1 k=1                 i=1      /      t1,t2,Si,j,k,Ti,j>0, i=1,I,j=1,J + 1,j=1,J,k=1,K subject to constraints (1)-(16), where c1, c2, c3 are some nonnegative constants. For c1 = c2 = c3 = 1, we get criterion (17), for c1 = 1, c2 = c3 = 0, we get the problem to minimize the total time of trains at railway hauls (in other words, the problem to minimize quantity of energy at transportation), for c1 = c2 = 1, c3 = 0, we get the problem to minimize total time of trains at the railway network segment from departure, for c1 = 0, c2 = 1, c3 = 0 we get the problem to minimize usage of resources at stations. For c1 = 1, c2 = c3 = 0 and c1 = 1, c2 = 1, c3 = 0, problems to make the transportation plan were formulated in [13]

earlier. In such a way, criterion (18) is more universal than criterion from [13]. At the same time, the quantity of variables in problem (18) with constraints (1) - (16) is about 2 times less than the quantity of variables in [13], and the quantity of constraints at the present paper is about K/7 + 1 times less than in [13].

4.    Algorithm to Find a Suboptimal/Initial Solution

We significantly reduced the quantity of constraints and variables in comparison with [13]. Nevertheless, it is still complicated to find the solution to problem (18) with constraints (1) – (16). Therefore, we propose the algorithm for finding suboptimal/initial solution to this problem.

Let us solve problem (18) with constraints (1) – (16) for some subset of trains. To this end, we consider sets

I m i m def {i e Z : 1 <  i < I, v dep = m i , vf ¹"' = m 2 }, m i = 1, M, m 2 = 1, M, characterizing numbers of trains having departure station index m ₁ and arrival station index m 2 . Obviously, some of these sets are empty. For example, I _m 1 ,_m 1 = 0, since for trains the departure vertex can not coincide with the destination vertex. Also, we note that

MM

I ^d = f {i e Z :1 <  i <  I } = U U I m i m .

Let S be a total quantity of nonempty sets among all sets I m ₁ ,m ₂ . Let us arrange nonempty sets I m ₁ ,m ₂ in ascending order of the quantity of elements in these sets (if two or more sets have the same quantity of elements then ordering occurs by minimal element in these sets). Renumbering these sets from 1 to S according to the introduced order, we obtain sets of indices I ₁ , . . ., I _S . Further, we solve the problem

• J+1 K                           J

• c i E E E 6 - j .k№^d - e   + C 2 EE T j +

i ∈ I 1 j=1 k=1                           i ∈ I 1 ˆj₌₁

K

I ^           min

δ i,j,k T^ˆ i,j ≥0 i ∈ I 1 j=1 J+1 ^ˆj=1 J k=1 K

+сз EE  ■ ktkeg. - E t i∈I1 k=1               i∈I1

with constraints (1) – (16). If solution to this problem does not exist, then the process of finding suboptimal solution is completed unsuccessfully. If solution exists, then we form the set K 1 that is the set of numbers of “subthreads” taken for traffic by trains with numbers from the set I 1 . Further, these “subthreads” will be excluded from scheduling by imposing additional constraints

• ⁶ - jkk = 0, i ^e I s , j = 1, J + 1, k ^e K I ,

where s e [2, S]. Thus, at the s-th step of the iterative procedure for finding suboptimal solution, we solve the problem

J +1 K                           J

• c i E E E ' - t k^eg. ) + C 2 EE T ij +

i ∈ I s j=1 k=1                           i ∈ I s ˆj=1

• +сз ( E ^E <-4 k t k eg. - E tT p ) ^    .       min

i∈Is k=1               i∈Is             δi,j,k Ti,j ≥0 i∈Is j=1 J+1 j=1 J k=1 K with constraints (1) – (16) and s-1

Sj = 0,i G Is, j = 17+1, k G |J Kp, p=1

where K _p is the set of “subthreads” taken by trains with numbers from the set I _p , obtained at the p-th step of the iterative procedure, p = 1, s — 1. If at some step of the iterative procedure there is no solution to the optimization problem, then the process to find suboptimal solution is terminated. At the same time, it is impossible to make conclusion about the absence of the solution to original problem (18) with constraints (1) – (16).

Based on reasonings above, we formulate the algorithm to find a suboptimal solution to problem (18) with constraints (1) – (16).

• 1.    Form sets Im1 m2 = {i G Z : 1 < i< I, v^dep.= m1, viarr. = m2}, m1 = 1,M,m2 = им.           ’

• 2.    Compute S that is the quantity of nonempty sets I_m1,m2. Nonempty sets I_m1,m2 should be arranged in ascending order of the quantity of elements in these sets (if two or more sets have the same quantity of elements then ordering occurs by minimal element in these sets).

• 3.    Renumber the sets I_m1 ,_m2 from 1 to S according the order from Step 2 of this algorithm, after that get sets of indices I₁, . . . , I_S.

• 4.    Initialize the parameter s = 1. Form the set K0 = 0.

• 5.    Solve problem (19) with constraints (1) – (16) and the constraints

• 6.    If s = S, then the process to find the suboptimal solution is terminated successfully. If s < S, then increase the parameter s by 1 and go to Step 5.

5. Example

s-1

5 ijk = 0,i Gl s , j = 17+1 ,k G U K p .

p=0

If a solution exists, then form the set of “subthreads” K _s taken by trains with numbers from the set I s and go to Step 6. If a solution does not exist, then the process to find the suboptimal solution is terminated unsuccessfully.

The specified algorithm is based on the work [15] in which it was proposed to construct a train timetable for a railway station sequentially, separately for each train.

Let us consider the railway network segment represented as the multigraph G shown in Figure. Some of edges are drawn with a dotted line in order to show a multilevel intersection of two railway tracks. The numeration of tracks in the figure is omitted: if two adjacent vertices are connected by two edges, i.e. two tracks, then the edge represented by a straight line has number 1, while the other has number 2.

Suppose that it is required to make the transportation plan for I = 62 trains. We indicate the vertices of the departure and destination of these trains in Table 1.

от )------------( 6 )-------------( 8 )-------------( Z )-------------( 9 )-------------( S

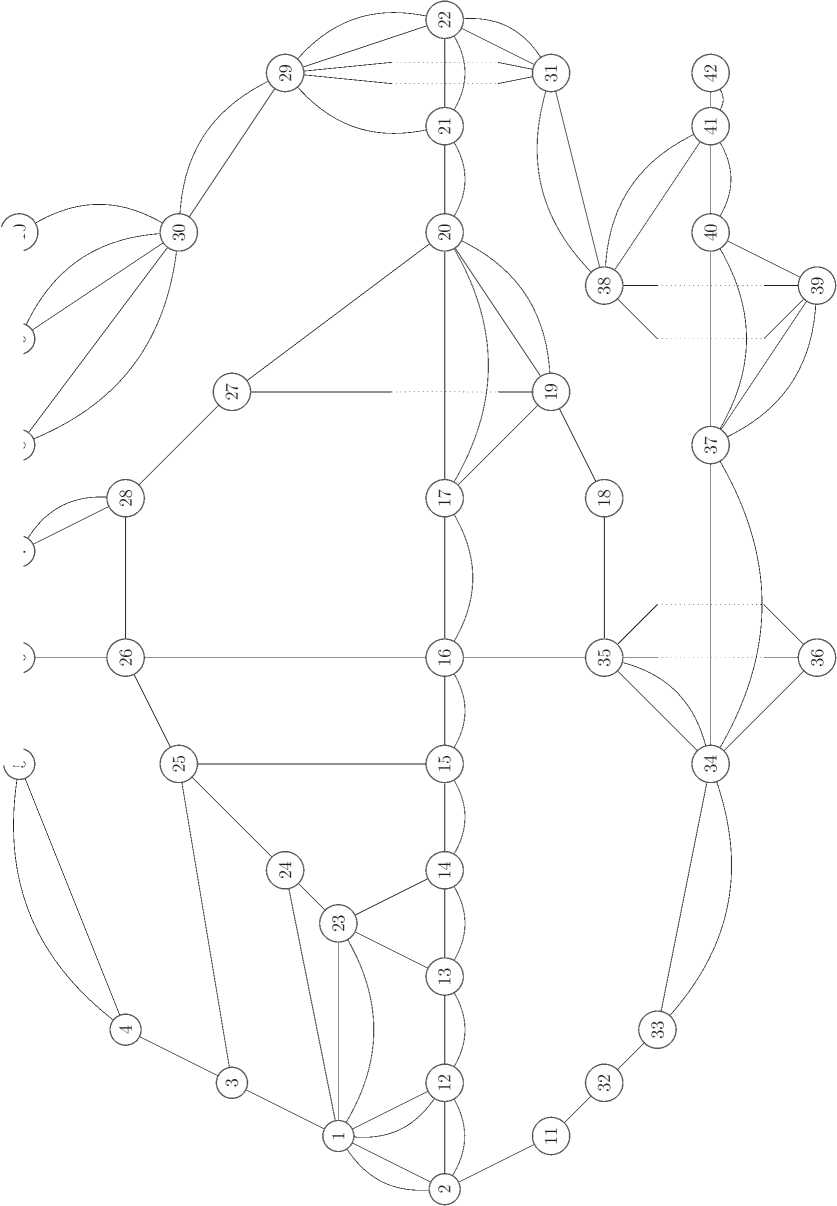
Multigraph G of the railway network segment

Train direction

Train direction (departure → destination)	Quantity of trains	Train direction (departure → destination)	Quantity of trains
2→10	13	10 → 2	13
2→ 22	8	22 → 2	8
34 → 42	7	42 → 32	7
34 → 33	2	2 → 33	1
10 → 42	1	42 → 10	1
5 → 34	1

Assume that there are K = 1249 “subthreads” for scheduling transportation plan.

Let the parameter J be equal to 12. At first, we compare time of searching for solution to problem (18) with constraints (1) – (16) when c ₁ = 1, c ₂ = 0, c ₃ = 0 and similar problem statement from [13] (when t 1 = t 2 = ∆ = 0). We set the minimal and maximal possible duration of stay at intermediate stations to be equal to 0 and 1440 minutes, respectively.

The experiment showed that if we consider the search for an optimal solution only for the first five trains in the list of trains, then the optimal solution to problem (18) with constraints (1) – (16) was found in 19 seconds. At the same time, for problem statement from [13], the iterative process of finding at least some feasible solution was not terminated in 2 hours. If we consider the search for an optimal solution only for the first train in the list of trains, then the optimal solution to problem (18) with constraints (1) – (16) was found in 3 seconds. For problem statement from [13], the iterative process of finding at least some solution was not terminated in 2 hours again.

Let us consider a problem to make the transportation plan for all of I trains (consider the case when c 1 = c ₂ = c ₃ = 1). Suppose that d i = 180, tf .min' = 0 and t Stkmax" = 120, i = 1 , I , k = 1 , K . Also, suppose that T _max. = 1440. In view of the large quantity of variables and constraints in problem (18) with constraints (1) – (16) and associated computational difficulties when searching for a solution, we use the presented above algorithm. As a result of applying the algorithm, we obtain train routes shown in Table 3.

As follows from Table 3, almost all trains with the same departure and destination vertices follow the same route. The only exception is movement between vertices with indices 2 and 10. The solution is reasonable from the point of view of traffic along the multigraph of the railway network segment. Namely, movement from the vertex with the index 34 to the vertex with the index 33 is not carried out through some intermediate stations, there are no “circular” routes for movement from 34 to 42 and back (for example, the vertex with the index 16 is not involved at the movement).

As follows from Table 2 and Table 3, 468 of 1249 “subthreads” are involved in the transportation plan. However, it is difficult to answer the question of how much more trains can be transported. It is caused by the fact that the possibility to transport an additional train depends not only on quantity of available “subthreads” but also on the time: the time when the train is ready for departure and the time of movement along a particular “subthread”.

The search time for the suboptimal solution was 18 minutes. All results were obtained using ILOG CPLEX mathematical package on the personal computer (Intel Core i5 4690, 3,5 GHz, 8 GB DDR3 RAM).

Set of “subthreads”

Direction (begin → end)	Quantity of “subthreads”	Direction (begin → end)	Quantity of “subthreads”	Direction (begin → end)	Quantity of “subthreads”
1→2	22	1→3	21	1 → 12	3
1 → 23	5	1 → 24	3	2→1	21
2→11	5	2→12	22	3→1	22
3→4	21	3→ 25	3	4→3	22
4→5	21	5→4	22	5→6	21
6→5	22	6→7	21	6→ 26	3
7→6	22	7→8	21	7→ 28	4
8→7	22	8→9	21	9→8	22
9→10	21	9 → 30	5	10 → 9	22
10 → 30	4	11 → 2	5	11 → 32	5
12 → 1	3	12 → 2	23	12 → 13	22
13 → 12	23	13 → 14	22	13 → 23	3
14 → 13	23	14 → 15	22	14 → 23	3
15 → 14	23	15 → 16	22	15 → 25	3
16 → 15	23	16 → 17	22	16 → 26	4
16 → 35	3	17 → 16	23	17 → 18	3
17 → 20	22	18 → 17	3	18 → 19	7
18 → 20	6	18 → 27	4	18 → 35	4
19 → 18	7	20 → 17	23	20 → 18	6
20 → 21	22	20 → 27	4	21 → 20	23
21 → 22	22	21 → 29	3	22 → 21	23
22 → 29	5	22 → 31	8	23 → 1	5
23 → 13	3	23 → 14	3	23 → 24	4
24 → 1	3	24 → 23	4	24 → 25	3
25 → 3	3	25 → 15	3	25 → 24	3
25 → 26	4	26 → 6	3	26 → 16	4
26 → 25	4	26 → 28	3	27 → 18	4
27 → 20	4	27 → 28	3	28 → 7	4
28 → 26	3	28 → 27	3	29 → 21	3
29 → 22	5	29 → 30	5	29 → 31	7
30 → 9	6	30 → 10	4	30 → 29	5
31 → 22	8	31 → 29	7	31 → 38	8
32 → 11	5	32 → 33	5	33 → 32	5
33 → 34	15	34 → 33	15	34 → 35	5
34 → 37	15	35 → 16	3	35 → 18	4
35 → 34	5	37 → 34	15	37 → 40	15
38 → 31	8	38 → 41	6	40 → 37	15
40 → 41	15	41 → 38	6	41 → 40	15
41 → 42	15	42 → 41	15

Conclusion

In this paper, we considered the problem to construct the optimal train timetable on the multigraph of the railway network segment. The new mathematical model of traffic on the multigraph of the railway network segment was proposed. An universal criterion was proposed to form the optimal timetable. The problem of constructing optimal timetable was reduced to a mixed integer linear programming problem that contains several times

Table 3

Train routes

Direction Quantity of trains Train route о __к 1 П 2 → 10 12 2→1→3→4→5→6→7→8→9→10 1 2→12→13→14→ 15→ 16→ 17→20→21→22→29→30→10 1П _к 9 12 10 → 9 → 8 → 7 → 6 → 5 → 4 → 3 → 1 → 2 10 → 2 1 10→30→29→22→21→20→17→ 16→ 15→ 14→ 13→ 12→2 2 → 22 8 2→12→13→ 14→ 15→ 16→ 17→20→21 →22 22 → 2 8 22→21→20→17→16→15→14→13→12→2 34 → 42 7 34 → 37 → 40 → 41 → 42 42 → 34 7 42 → 41 → 40 → 37 → 34 34 → 33 2 34 → 33 2 → 33 1 2 → 11 → 32 → 33 10 → 42 1 10 → 9 → 30 → 29 → 22 → 31 → 38 → 41 → 42 42 → 10 1 42 → 41 → 38 → 31 → 22 → 29 → 30 → 9 → 10 5 → 34 1 5→6→26→16→17→18→35→34 fewer variables and constraints than the similar problem from [13]. This reduction in dimension made it possible to find the solution to the problem of constructing optimal timetable much faster. The algorithm to find a suboptimal solution was proposed. Its applicability (in terms of time to find a solution) was demonstrated with a meaningful example. In the future, it is possible to construct other algorithms for finding suboptimal solution in order to accelerate the search for a suboptimal timetable, as well as joint search for train timetables and “track possession” within the framework of the proposed mathematical model of traffic along the multigraph of the railway network segment.

Acknowledgement. This work was supported by the Russian Foundation for Basic Research, project No. 20-07-00046 A.