On topological structure of some sets related to the normalized ricci flow on generalized Wallach spaces

1. Introduction and the Main Result

It is known that determining the connectedness (or the number of connected components) of real algebraic surfaces is a. very hard classical problem in algebraic geometry (see e. g. [4, 13]). In this paper we deal with similar problems relating to the normalized Ricci flow on generalized Wallach spaces. The importance of these problems is due to the need to develop a. special apparatus for studying general properties of degenerate singular points of Ricci flows initiated in [1-3]. More concretely, in the above papers, the authors considered some problems concerning the topological structure of the sets (0,1/2)3 П D and (0,1/2)3 \ D, where

D = {(ai, a2, аз) E R3 : Q(ai, a2, аз) = 0} is an algebraic surface (see Fig. 1 and 2) in R3 defined by a symmetric polynomial Q(a1, a2, аз) in a1,a2, аз of de give 12:

Q(ai, a2, аз) = (2si + 4s3 — 1) (64s1 — 64s1 + 8s³ + 12s² — 6si + 1

+ 240s3s1 — 240S3S1 — 1536s^s1 — 4096s3 + 6OS3 + 768s^)

• —    8si (2s 1 + 4s3 — 1)(2s 1 — 32s3 — 1)(10s 1 + 32s3 — 5)s2                 (1)

• —    16s1(13 — 52s1 + 640s3s1 + 1024s2 — 320s3 + 52s1)s2

+ 64(2s1 — 1)(2s1 — 32s3 — 1)s3 + 2048s1 (2s1 — 1)s2, s1 = а1 + а2 + аз,  s2 = а№ + а1аз + а2аз, s3 = а^аз.

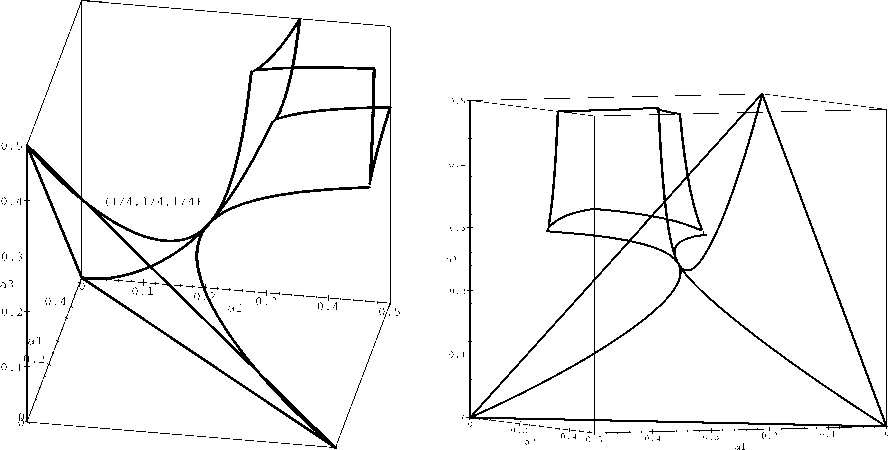
Fig. 1. Singular points of the surface (0,1/2)3 П Q.

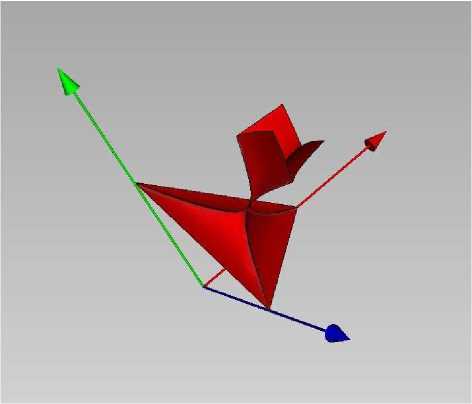
Fig. 2. The surface (0,1/2)3 П Q.

The surface Q naturally arises in studying of general properties of degenerate singular points of the following dynamical system (see [1-3]):

dx1                   dx2dx3

—- = f (xi,x2,xa), — = g(xi,x2,xa),  -v- = h(xi,x2,xa),U)

dt                      dtdt where xi = xi(t) > 0, i = 1, 2, 3.

f (x1, x2, x3) =	x1 — 1 — a1x1 ---- x2x3	- x2 x1x3	- x3 x1x2	+ xiB,
g(x1, x2, x3) =	x2 1    a2X2 1 x1x3	- x3 x1x2	— _^1_ ) x2x3	+ X2B,
h(x1, x2, x3) =	x3 1   a3x3 I x1x2	x1 x2x3	— ^^) x1x3	+ x3B,

B := (—+ —+ — — (— + — + —(— + — + —) a x    a2x2   a3x3     x2x3 x x3   x x2      a    a2   a3 ai E (0,1/2],    i = 1, 2, 3.

It should be noted that the system (2) can be obtained from the normalized Ricci flow equation

g (t) = —2Ricg +2 g (t) Sg,

∂t                     n where g(t) moans a 1-parameter family of Riemannian metrics. Ricg is the Ricci tensor and Sg is the scalar curvature of the Riemannian metric g, considered on one special class of compact homogeneous spaces called three-locally-symmetric or generalized Wallach spaces, see [9, 12]. In the recent papers [7] and [11], the complete classification of these spaces was obtained.

A more detailed information concerning geometric aspects of this problem and the Ricci flows could be found in [8-10] and [14].

In [1], the authors noted that the set (0,1/2)3 П Q is connected, and the set (0,1/2)3 \ Q consists of three connected components O1, O2 and O₃ (see Fig. 1) containing the points (1/6,1/6,1/6). (7/15, 7/15, 7/15) and (1/6,1/4,1/3) respectively.

The present work is devoted to detailed proof of this observation. The main result is the following

Theorem 1. The following assertions hold with respect to the standard topology of R³ :

• (1)    The set (0,1/2)3 П Q is connected.

• (2)    The set (0,1/2)3 \ Q consists of three connected components.

• 2.    Proof of the Main Result

We note also the following

Corollary 1. The assertions of Theorem 1 are preserved if (0,1/2)3 is replaced by (0,1 /2]³.

Remark 1. The symmetry of Q with respect to ai, a₂, аз implies the invariance of Q under the permutation a1 ^ a₂ ^ аз ^ a1.

Remark 2. Proof of Theorem 1 is based on the idea of Remark 8 in [2]: One should consider a segment I with one endpoint at (0,0,0) and with the second endpoint at an arbitrary point of any facet of the cube (0,1/2)3 containing (1/2,1/2,1/2). According to Remark 1, we can assume without loss of generality that I is defined by the following parametric equations ai := at, a2 := bt, аз := t/2,                                (3)

where t E [0,1]. a, b E (0,1/2). Substituting (3) into (1) rve obtain some polynomial p(t) := Q(at, bt, t/2) in t of degree 12. Thus the problems under consideration could be reduced to the problem of determining the possible number of roots of p(t) in [0,1] when (a, b) E (0,1/2)2.

Using Maple we have the following explicit expression for p(t):

p(t) = —256b²a²(2a + 1)² (2b + 1)²(b + a)²t¹² + 32(16b³ a³ + 4b³ a² + 2b³ a + 2b³ + 8b² a² + b²a + 4b² a³ + 2ba³ + ba² + 2a³)(2a + 1)(2b + 1)(2b + 1 + 2a)(b + a)t¹⁰ - 32(2a + 1)(2b + 1)(b + a)(16b³a³ + 4b³a² + 2b³a + 2b³ + 8b²a² + b²a + 4b²a³ + 2ba³ + ba² + 2a³)t9 - (72b²a² + 104ba³ + 208b³a² + 104b³a + 208b²a³ + 52b⁴ + 176a4b + 208b4a² + 176b4a + 52ba² + 52b² a + 208a4b² + 52a⁴ + 352b³ a³ + 13b² + 13a² + 44a³ + 44b³ + 22ba)(2b + 1 + 2a)2t⁸ + 2(2b + 1 + 2a)(72b2a² + 104ba³

+ 208b3 a2 + 104b3 a + 208b2 a3 + 52b4 + 176a4 b + 208b4a2 + 176b4 a + 52ba2

+ 52b2 a + 208a4 b2 + 52a4 + 352b3 a3 + 13b2 + 13a2 + 44a3 + 44b3 + 22ba)t7

+ (600b2 a2 + 392ba3 + 784b3 a2 + 392b3 a + 784b2 a3 + 108b4 + 14b + 14a + 128a6

+ 448ba5 + 224a5 + 528a4 b + 432b4a2 + 528b4 a + 196ba2 + 196b2 a + 432a4b2 + 108a4 + 288b3 a3 + 224b5 + 448b5 a + 128b6 + 2 + 27b2 + 27a2 + 36a3 + 36b3 + 66ba)t6

• — 6(8b³ + 4b² a + 2b² + 8ba + b + 4ba² + 2a² + 8a³ + 1 + a)(2b + 1 + 2a)2t⁵ + (2b + 1 + 2a) (40b³ + 24ba + 5 + 40a³)t⁴ + (22b + 22a + 88ba² + 88b² a + 2 + 44b² + 44a² + 16a³ + 16b³ + 80ba)t³ — 6(2b + 1 + 2a)2t² + (8a + 8b + 4)t — 1.

Consider the following set

K := {(a, b) E R² : a,b E (0,1/2)}.

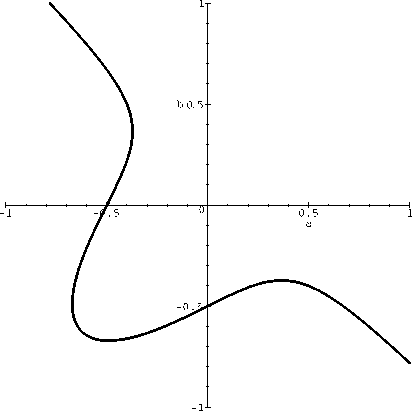
Fig. 3. The curve y-

Lemma 1. If (a, b) E K then the discriminant D of the polynomial p(t) equals to zero if and only if a = b.

• <1 Easy calculations show that D is non-negative, moreover, D has the same zeroes as the following polynomial:

(2b — 1)12(2a — 1)12(a — b)12(F (a,b))2,                            (5)

where

F(a, b) := 40a³ - 24a2b - 24ab² + 40b³ - 12a² + 12ba - 12b² - 6a - 6b + 5.

Denote by y the curve determined by F (a, b) = 0 (see Fig. 3). Al e will prove that y Ims no common point with the square K.

Changing the variables by the formula x - y = a V2, x + y = b V2 , we get a new equation for y, from that we can express y explicitely:

F(x,y) :=36(8x - V2 )y2 + (8x + 5^2 )(2x - ^2 )2 = 0.              (C)

Note that the point (x‘,y‘) = (V2/2, 0) belongs to y, moreover, this is an unique singular point of y- Since

22   22                 ____

FxxFyy ^- Fxy = ³⁸⁸⁸ > ⁰

at (x‘,y‘), then (x‘,y‘) is isolated according to the well-known result in differential geometry of planar curves. It is clear that the point (a, b) = (1/2,1/2) / K corresponds to (x‘,y‘) in the initial variables.

It is obvious that every regular point of y satisfies the condition x < x₀ := V2/8. Hence only we need is to show that y ^{can n}°t intersect the part of K, described by the conditions x G (0,xo). -x < y < x. In fact, it suffices to prove the inequality x < ^(x). where

F(x):=

2x 1 8x + 5 У2 V V2 - 8x

is a function determining a part of the curve y in (6)- Note that limx ,_x0 ₀ ^(x) = +to. It is easy to show that the inequality x < ^(x) is equivalent to the inequality

^(x) := 320x3 - 48^2 x2 - 24x + 10^2 > 0, which holds for all x G (0, xo). siiice ^(x) is positive at x = xo arid decreases:

^ (xo) = 27V2/4 > 0, /(x) = 960x2 - 96V2x - 24 < 0.

Therefore. F(a, b) = 0 for (a, b) G K. Hence there is a unique possibility a = b in order to D = 0 111 K by (5 ). ▻

Lemma 2. Let (a, b) G K. Then a point of local extremum of p(t) can not be a multiple root of p(t).

• <1 Multiple roots of p(t) are possible only for a = b by Lemma 1. Therefore, we may assume that b = a. Then (4) takes the following form

P(t) = -(t + 1) P2(t) P3(t), p2 (t) := (2 + 4a)t2 - 2(1 + 2a)t + 1, p3(t) := 8a2(2a + 1)t3 - (1 + 4a)t + 1.

Denote by D2 aiid D3 the discriiniiiaiits of p2(t) aiid pa(t) respectively:

D2 := 4(2a + 1)(2a - 1), D3 := -32(2a + 1)(2a - 1)(22a2 + 14a + 1)a2.

Since D2 <  0. D3 > 0 for a E (0,1/2). then it is clear th at the polynomial p(t) has exactly three distinct real roots (each of multiplicity 3) for every such a. It follows from this fact that there is no points of local extrema of p(t) among the roots of p(t). >

Further we need the curve Г (see Fig. 4), which can be obtained as a result of the intersection Q with the plane аз = 1/2 for 0 < ai,a2 C 1/2- Recall some properties of Г (see details in [2]): Г determined hr" the equality G(a1,a2) — 0. where

G(ai, a2) :— 4(ai + a2)(4aia2 — 1)(4aia2 — ai — a2 + 1)(4aia2 + ai + a2 + 1) + (16a^a2 + 1)(13a1 + 22aia2 + 13a2) — 4(a1 + a2)(11a1 + 18aia2 + 11a2),

Г is homeomorphic to the segment [0,1] with the endpoints (V2/4,1/2). (1/2, V2/4) arid with the unique singular point (a cusp) at (a1,a₂) — (a, a), where a :— (V5 —1)/4 ~ 0.3090169942.

It is easy to check that Г separates K into disjoint connected components K1 and K2 containing the points

(a‘,b‘) :— (3/10, 3/10) and (a‘‘,b‘’) :— (31/100, 31/100)

respectively.

o.i-

0            0.1          0.2          0.3          0.4          0.5

Fig. 4. The intersection П with the plane a₃ = 1/2 for 0 <  a1,a₂ C 1/2-

Lemma 3. In the segment [0,1], the polynomial p(t) has

(!) one root, if (a,b) E K1:

• (2) two distinct roots, if (a,b) E K₂ U Г.

• <1 Lel. t* E [0,1] be a 1 'oot of p(t) given by (4). We say that t* is a robust root of p(t) in [0,1]. if small perturbations of the parameters a ami b imply a, small perturlmtion of t* keeping it in (t* — e, t* + e) C [0,1] for some small e >  0 (see e. g. [6] for more details on singularities of curves and some related problems).

Now, assume that t* is a non-robust root of p(t). Then there exist exactly two possibility (recall that t* E [0,1]):

Case 1. t* — 0 0r t* — 1;

Case 2. t* belongs to the interval (0,1) and pi-ovides p(t) a local extremum.

Now, we consider these cases separately.

Case 2. Assume that t* is a point of lot-al extremum of p(t). Tlion t* is a multiple root of p(t). This contradicts to Lemma 2, hence, the case 2 is impossible.

Case 1. Since p(0) = —1 then there exists no pair (a, b) such that t = 0 is a r<>ot of p(t).

Suppose that t = 1 is a r<>ot of p(t). Since

p(1) = —4(a + b)2G(a, b), where G is given by (7). then the equality p(1) = 0 is possible if' and only if G(a,b) = 0.

Recall that the curve Г is determined by G(a, b) = 0. Si nee p(t) has only robust roots for every pair (a, b) € Ki U K by our construction, the 11 the number of roots of p(t) in [0,1] is constant both in Ki and in K2. Hence, it is sufficient to calculate the number of such roots only for the representative points (a‘,b‘) € Ki and (a‘‘,b‘’) € K2.

• (1)    Suppose that (a, b) = (a‘,b‘) € K1- Then (4) takes the following form

  P(t) = - 9765625 (t ⁺ 1)(16t2 - 16t ⁺ 5)(144t3 - 275t + 125)3*

Taking into account Lemma 2, we conclude that p(t) has three distinct real roots of multiplicity 3 besides the root t = —1. Since we does not need exact values of these roots then their approximated values are:

—1.569348118, 0.5345099430, 1.034838175.

• (2)    Now. suppose that (a, b) = (a‘‘,b‘’) € K₂. Then in (4) we obtain

  p(t) =

  
  
  
  

  (t + 1)(81t²

  
  

  — 81t + 25)(77841t³ — 140000t + 62500)3,

  
  

with the following real roots (of multiplicity 3):

—1.524828329 ..., 0.5285082631..., 0.9963200660 ...

It is easy to see that for (a, b) € Г the polynomial (4) has two roots in [0,1], one of which is 1 by the definition of Г.

Hence, in the segment [0,1], the polynomial (4) has one root for (a, b) € Ki and two roots for (a, b) € K2 U Г. >

• <1    Proof of Theorem 1 is based 011 Lemma 3 and Remark 2. Lei, (a, b) € K. Then the number of intersection points of H with the segment I equaIs to 1 or 2 depending on the number of roots of the polynomial p(t) (see (4)) containing in [0,1].

• (1)    Connectedness of the set (0,1/2)3 П H. Let t1,t₂ be roots of p(t) such that 0 < t1 < t₂ ^ 1. Then, 0bviously, t1 and t₂ correspond to the “lower” and “upper” (see Fig. 2) parts of the surface H П (0,1/2)3 respectively. These parts of H have a unique common point (a1,a₂,a3) = (1/4,1/4,1/4) (an elliptic umbilic of H according to [I]).

• (2)    The number of the connected components of the set (0,1/2)3 \ H. Since the maximal number of roots of p(t) in [0,1] is equal to 2 and H П (0,1/2)3 is the union of two surfaces with one common point, then the number of connected components of (0,1/2)3 \ H equals to 3. Theorem 1 is proved. >

In order to prove Corollary 1 we need the following

Lemma 4. Let b = 1/2. Then in the segment [0,1], the polynomial p(t) has

(!) one root for a € (0, V2/4) ;

• (2)    two roots for a € [V2/4,1/2) ;

• (3)    one root (of mull ipliciiy 8) f)r a = 1/2.

<1 (1), (2) .It b =1/2. a G (0,1/2) - ■ have

P^(t) = ^{— (2ta +} 1) P2^(t) P3^(t)

in (4), where p₂(t) := 4a(2a + 1)t² — 2(1 + 2a)t + 1,

P3(t) := 2(1 + 2a)t³ — 2(a + 1)t + 1.

For the discriminants D2 and D3 of the polynomials p₂(t) and P3(t) we have

D2 := —4(2a — 1)(2a + 1) > 0,

D3 := 4(2a + 1)(2a — 1)(8a2 + 28a + 11) < 0.

Since the cubic polynomial P3(t) achieves a positive local maximum at the point t = — ^a^aAa^) < 0, then its unique real root must be a negative number. Therefore, the required roots of P(t) can be pros’ided only by P2(t). moreover. first of them belongs to [0,1] for all a G (0,1/2): the second of them — only for a G [V2/4,1/2).

• (3)    The case b = a = 1/2 leads (4) to the polynomial

P(t) = —(t + 1)4(2t — 1)8

with the unique root t = 1/2 of multiplicity 8 on [0,1]. It should be noted that we get an elliptic umbilic (a1,a₂,a3) = (1/4,1/4,1/4) of the surface Q in tins case. >

• < Proof of Corollary 1. According to Theorem 1 it is sufficient to consider the case when a = 1/2 0r b = 1/2. Taking into account Remark 1, assume without loss of generality that b = 1/2. Thon the proof of Corollary 1 foilows from Lemma 4 and Remark 2. >

Remark 3. When this paper had been written the author was informed about the recent paper [5], where a more detailed description of the surface Q was obtained without the restriction (ai,a2,a3) G (0,1/2)3.

The author is indebted to Prof. Yu. G. Nikonorov and to Prof. A. Arvanitoyeorgos for helpful discussions concerning this paper.